浮动簧的抗疲劳和可靠度分析

周 威，王 刚

（中北大学 机电工程学院，山西 太原 030051）

0 引言

随着自动武器的快速发展，人们对自动武器各方面的性能提出了越来越高的要求。为降低武器射击的后坐力和提高射击精度，浮动技术被广泛应用于自动武器的反后坐中。浮动机是实现浮动射击的装置，常见的浮动机类型有以弹簧作为弹性介质的弹簧式浮动机，也有以弹簧和其他材料作为弹性介质的弹簧液压式和弹簧摩擦垫式浮动机等［1］。在这些类型的浮动机中，浮动簧都是必不可少的一部分，其抗疲劳强度和可靠性直接关系到整个浮动机能否稳定可靠的工作。

1 浮动簧断裂失效的原因分析

通过对浮动簧原材料外观检查，发现其表面有锈蚀和结疤。用酸浸法进一步检查发现材料表面有裂纹，材料的表面粗糙度越大，其疲劳极限下降的越多。其次，由于浮动簧一般使用车床绕制，受装夹和心轴限制，使得加工后的弹簧表面出现划痕。另外，防锈措施的不全面也会导致弹簧表面形成凹痕，其中的夹杂物是应力集中源，在弹簧工作过程中会导致基体界面与夹杂物之间产生疲劳裂纹。最后，喷丸强化处理不彻底也会导致表层产生的残余拉应力不能有效消除，从而影响工作寿命。

2 浮动簧断裂失效的可靠度分析

浮动簧工作时，裂纹可能会逐渐扩大导致弹簧断裂，在弹簧的可靠度分析中以应力强度因子k1表示裂纹尖端区域的应力场强度，以应力强度因子幅度Δk1作为描述促进疲劳裂纹扩展的参数。Δk1的表达式为：

其中：k1min，k1max分别为应力强度因子的最小值和最大值；a为裂纹尺寸；α为修正系数，与裂纹的受力条件和几何因素相关；σmin，σmax分别为作用于构件上的应力最小值和最大值。疲劳裂纹扩展特性可用应力强度因子幅度Δk1与裂纹扩展速率da/dN（N为变负荷作用次数）的对数关系曲线描述［2］。疲劳裂纹扩展特性曲线如图1所示。

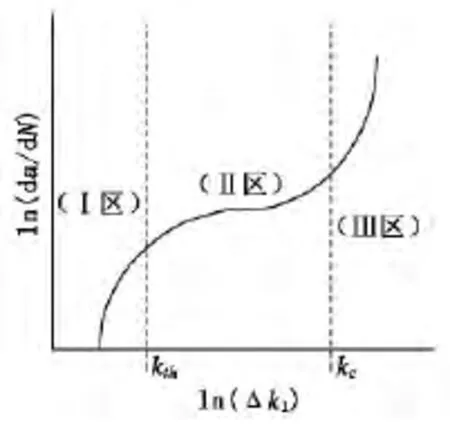
图1 疲劳裂纹扩展特性曲线

由图1可知，Δk1＜kth（I区），裂纹不会扩展，门槛值kth的大小取决于受到的平均应力大小和材料自身的性能；当Δk1≥kth时（II区），裂纹扩展的速率缓慢增大；当Δk1的值增加到一定程度时（III区），裂纹扩展速率急剧增加。当Δk1的最大值Δk1max超过弹簧的断裂韧性kc（kc表示材料对裂纹扩展的抗力，其值取决于材料本身的性质）时，弹簧断裂。从力学角度考虑kc又是应力强度因子幅度Δk1的临界值，当Δk1＝kc时，裂纹体处于临界状态，即将断裂。本文所进行的浮动簧抗疲劳断裂研究是在kth≤Δk1＜kc的范围内（II区）进行的。

3 浮动簧的抗疲劳设计

在浮动机中弹簧件采用较多，而且要求全部为全寿命件，即工作寿命同浮动机寿命相同，所以需要对浮动簧进行抗疲劳设计。在目前技术水平下，抗疲劳的主要措施是强压处理，强压处理的方法是将弹簧压并，并保持一定的时间。经过压并，使弹簧材料表层产生反向残余应力，提高了弹簧的承载能力。

3.1 强压弹簧的适用范围

强压压缩弹簧极限应力的选择范围应在强压稳定区内，表征该区域的标志是强压系数Qy，且有Qy＝τb/σb，其中，τb为压并应力，σb为材料抗拉强度。

强压系数Qy与弹簧材料及旋绕比C有关。Qy值应在大于等于0.45但小于表1规定的范围内选取。另外，强压弹簧只适合于有限寿命次数，一般不应超过2×104次［3］。

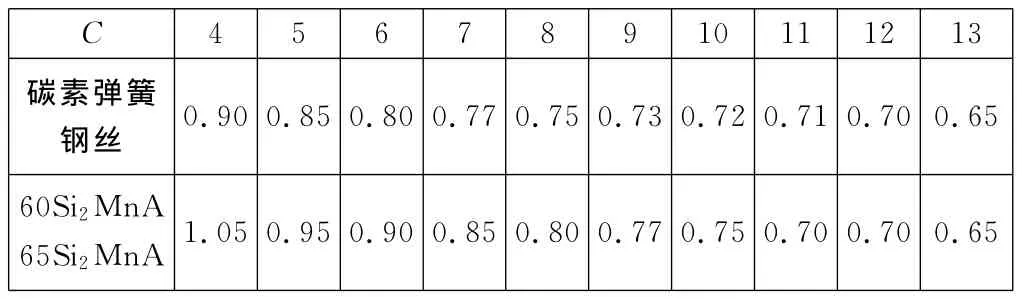
表1 Qy值应小于的值

3.2 疲劳强度校验

假设浮动簧在负荷P1和P2之间不断循环变化时，弹簧内部所产生的最大和最小循环交变剪切应力为：

其中：K为曲度系数；D2为弹簧中径；d为钢丝直径。

疲劳强度的安全系数n应满足下式：

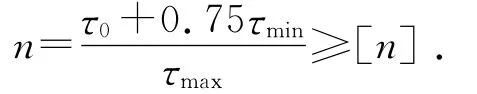
其中：τ0为弹簧材料的脉动疲劳极限，在变负荷作用次数N＝104次时，τ0＝0.45σb；［n］为许用安全系数，当弹簧设计计算精确、材料数据可靠时，取［n］＝1.3～1.7，否则取［n］＝1.8～2.2。

若已知kc和工作应力，可以求出弹簧的临界裂纹尺寸ac，即允许的最大裂纹尺寸，其值可由下式估算：

该裂纹判据可以定量地评估弹簧中出现裂纹后的安全性。

4 计算举例

设计一个浮动簧，该浮动簧的工作变形量为Fz＝76mm，安装高度H1＝70.5mm，要求工作负荷P2＝315N，弹簧中径D2≤30mm，材料采用60Si2MnA，对应的抗拉强度σb＝1 569N·mm－2。根据WJ/Z203标准可知弹簧的弹性模量G＝78 453N/mm2。

（1）初选钢丝直径d，计算弹簧旋绕比C及弹簧有效圈数m：初选d＝3mm，则C＝D2/d＝10，而曲度系数K＝（4C－1）/（4C－4）＋0.615/C＝1.145，圈数m＝Gd4F2/（8D23P2）＝7.1，取m＝7圈。

（2）计算压并应力τb：压缩弹簧的工作变形量F2应在压并变形量Fb的20%～80%之间的范围内选取。取F2＝0.8Fb，则Fb＝F2/0.8＝95mm；又取P2＝0.8Pb，其中Pb为压并压力，则Pb＝P2/0.8＝394N。由此可得：

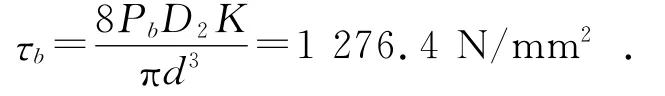
（3）验算强压系数Qy：已知σb＝1 569N/mm2，未进行强压处理前，强压系数Qy＝τb/σb＝0.813 5，查表1可知C＝10时，Qy＞0.75，不满足要求。经过强压处理，在相同的工作条件下，可以将弹簧的疲劳强度提高5%～35%。取抗疲劳强化系数β＝1.1，此时的强压系数Qy＝τb/（βσb）＝0.739＜0.75，满足强度要求。已知60Si2MnA的断裂韧度kc为75MPa·m1/2，强化后浮动簧的抗拉强度为1 725.9N/mm2，则浮动簧工作时的临界裂纹尺寸为ac＝0.25（75/1 725.9）2＝4.72mm。

5 结论

通过对浮动簧进行抗疲劳设计，可以提高浮动簧的承载能力，相比于未经强压处理的弹簧，在设计中更容易满足所要求达到的各个指标。

［1］王文记，赵国豪，赵舅，等.国内外高炮浮动技术的现状与发展趋势［J］.火炮发射与控制学报，2007（3）：69-72.

［2］张强.喷油煤浆泵塞弹簧抗疲劳断裂研究［J］.矿业研究与开发，2007（2）：44-46.

［3］梁世瑞.现代火炮自动机技术［M］.北京：兵器工业出版社，1995.