水下枪械内弹道基本方程组的建立及MATLAB仿真

兰晓龙，郝秀平，张小石，蒋泽一

（中北大学 机电工程学院，山西 太原 030051）

0 引言

通过陆地枪械发射内弹道经典方程组的建立，可得出弹道曲线p－t，v－t，p－x。这几条曲线反映了膛内压力的变化规律和弹丸速度的变化规律，使我们能够较深入地了解陆地枪械工作时的内弹道特性。而目前根据战争的需要，有些武器转战水下，为了能更深入地了解水下枪械工作时的内弹道特性，必须以陆地枪械发射内弹道经典方程组理论为基础，建立适合水下枪械内弹道的物理和数学模型，即水下枪械内弹道基本方程组。

1 水下枪械的内弹道分析与研究及方程组的建立

由于工作介质的改变，常规枪械弹丸的运动情况与水下枪械弹丸的运动情况有着显著的不同。为了使弹丸在水中运动具有良好的稳定性且不做高速旋转，选用滑膛式枪管，弹丸选用箭型。当火药点燃以后，火药燃气除了推动弹丸外还要推动弹丸前端的水柱一起运动。图1为水下枪械的内弹道简化模型。

图1 水下枪械的内弹道简化模型

图1中，lψ为药室自由容积的缩径长，x为弹丸在膛内的位移，l为弹丸的等效长度，lg为弹丸在膛内的全行程。

根据上述分析，为了简化过程并得出比较实用的模型，提出以下假设：

（1）燃烧的火药服从燃烧几何定律，即：

其中：ψ为已燃烧火药的相对质量；z为已燃火药的厚度；χ、λ均为火药的药型系数。

（2）不论是弹丸的运动还是火药的燃烧，都是在平均压力的情况下进行的。

（3）膛内的压力与火药的燃烧速度成正比关系，即：

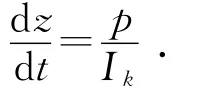
其中：p为火药燃气的压力；Ik为火药燃气压力的全冲量。

（4）膛内弹丸的速度与膛内水柱的速度相同，即：

其中：v为水柱和弹丸的速度。

（5）不论是火药燃烧期间还是燃烧结束后，燃烧生成物的成分始终保持不变。

（6）减小火药力f或增加绝热指数K的值，可以间接修正枪管内膛表面的热散失。

（7）水的密度不受枪械发射时散出的热量影响。

（8）各种形式的次要功用φ考虑。

根据以上假设应用牛顿第二定律以“弹丸和弹丸前枪管内的水柱”为研究对象得到膛内弹丸的运动方程为：

其中：S为枪膛横截面积；m为弹丸质量；ρ为水的密度。

综上所述，可以得到水下枪械内弹道的能量方程为：

2 计算仿真结果

运用MATLAB软件对某型号水下枪械进行数值仿真计算，可以得出p－t，v－t，p－x曲线，如图2～图4所示。

图2 p－t曲线

图3 v－t曲线

图4 p－x曲线

从图2中可以看出火药燃气的压力达到峰值286 MPa时经历的时间为0.6ms，弹丸在膛内的时间为2.5ms。从图3中可以看出256.8m/s为弹丸出管口的速度。从图4中可以看出火药燃气的压力达到最高值时是在弹丸在膛内运动了0.03m处，其数值高于常规枪械，且速度上升较快，这是由于膛内有了水柱的存在导致了弹后空间容积和弹丸位移增加较慢，从而带来了膛内压力的快速提高。

3 结论

通过对水下枪械内弹道的动力学建模、仿真可以得到以下结论：水下枪械内弹道特性与常规枪械内弹道特性的不同之处在于膛内弹丸的速度提升比较慢，膛内压力上升的速率比较快。

［1］吴望一.流体力学［M］.北京：北京大学出版社，1983.

［2］金志明.枪炮内弹道学［M］.北京：北京理工大学出版社，2004.

［3］王昌明，孔德仁，柳光辽，等.水下枪械内弹道分析及其理论建模［J］.弹道学报，1998，10（3）：1-5.