基于Simulink的电动汽车用感应电动机的控制仿真

王英豪，李 炜

（1.西南交通大学 机械工程学院，四川 成都 610031；2.华电电力科学研究院，浙江 杭州 310030）

0 引言

当前电动汽车的驱动电机有很多种，感应电机凭借其自身体积小、效率高、转速快等特点而被广泛采用，但对其进行精确控制是目前亟需解决的问题。本文在矢量控制技术的基础上分析并提出了一种电动汽车电机的控制方案，即在Simulink中对电机控制系统的功能单元分别建立独立的功能模块，将这些模块整合后组成电机系统的仿真模型。对其速度环采用闭环PID控制，利用仿真方法分析其动态性能。

1 矢量控制原理

矢量控制又叫磁场定向控制，本文采用相对比较方便的转子磁场定向控制方法。对于感应电动机，转子是短路的，故可以建立电压方程：

其中：R1为定子绕组电阻；R2为转子绕组电阻；Ls为定子绕组自感；Lr为转子绕组自感；Lm为定子和转子绕组间的互感；p为微分算子；ωs为转差频率；ω1为电机机械角速度；um1、ut1分别为两相静止坐标系下定子电压的两个分量；im1、it1分别为两相静止坐标系下定子电流的两个分量；im2、it2分别为两相静止坐标系下转子电流的两个分量。转矩方程为：

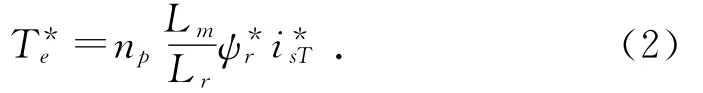
其中：为 给 定 转 矩；为 磁 链；为 转 矩 电 流 分量；np为电机极对数。

当磁链恒定时，转矩输出只由决定。由此可看出在整个控制过程中，磁链和转矩是分开控制的，即实现了完全解耦。

如图1所示，感应电动机的电流先后经过Clark变换和Park变换后得到励磁电流iM和转矩电流iT，再通过转矩和磁通计算模块得到磁通ψr和转矩Te，并通过编码器测定感应电动机的转速。转速调节器的输入是给定转速和测定转速的差值，转速调节器的输出为转矩给定值。根据这个值就可以计算出定子电流转矩分量的给定值，同时根据磁链给定值计算出定子电流磁通分量的给定值。将这两个分量送到Park逆变换计算出在两相静止坐标系下的给定电流，再送到电流滞环模块，输出6路PWM信号去控制3个逆变桥，进而控制电机，这就是整个模型的控制思路。

2 电动汽车仿真控制模型的建立

2.1 矢量控制坐标变换模块

坐标3/2变换模块把检测到的三相静止坐标系下的电流变换为两相旋转坐标系下的电流，实现解耦，进而得到类似于直流电机的控制，计算方程如下：

其中：ia，ib，ic为三相电流；id，iq为解耦分解电流；θ为角位移。根据式（3）建模如图2所示。

坐标2/3变换模块将电流从两相同步旋转坐标变换到三相静止坐标，计算方程如下：

2.2 定子电流磁通分量计算模块

本文是基于转子磁场定向的矢量控制方法来实现电机转速的控制，其基本思想是将定子电流解耦为电流磁通分量和电流转矩分量，磁链采用开环设计，计算方法如下：

图1 电动车矢量控制系统图

图2 坐标3/2变换计算模块

图3 坐标2/3变换计算模块

因此可以根据设定的磁链值ψ＊r来求出电流磁通分量的给定值i＊SM，其模型如图4所示。

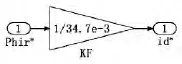
图4 磁通分量计算模块

2.3 定子电流转矩分量计算模块

根据转矩方程（2）得到电流转矩分量计算公式：

根据式（6）建模如图5所示。

图5 转矩分量计算模块

2.4 转子磁链角计算模块

此模块实现磁场定向角的计算，进而实现对磁场的定向，磁场定向方程为：

其中：φs为磁场定向角；Tr＝Lr/R2。由此可计算出φs，模型如图6所示。

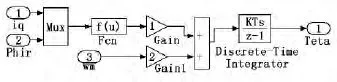
图6 磁场定向角计算模块

2.5 电流滞环模块

此模块的输入为三相电流给定值和测量值，输出为对应桥臂的脉冲。设置其环宽为2Δimax（Δimax为最大电流偏差），如果给定值电流大于测得电流，且超过Δimax，则此相下桥臂关闭，经过适当延时后，上桥臂打开，反之亦然，这样反复的通断，实际电流就会跟随给定电流，该模块如图7所示。

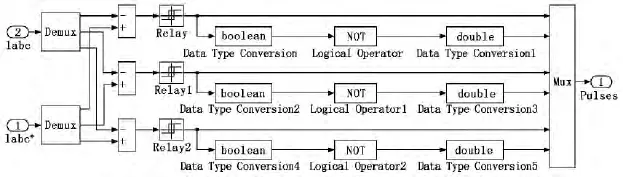
图7 电流滞环模块

2.6 速度控制模块

图8为速度控制模块，它实现对电动汽车车速的闭环控制，输入为汽车给定速度和电机反馈速度，把速度的差值送到比例环节和积分环节，输出转矩控制信号，并附加转矩限幅器，防止给定转矩信号突然过大。

2.7 负载转矩计算模块

根据汽车理论，电动汽车的行驶阻力方程为：

其中：Ff为滚动阻力；Fw为空气阻力；Fi为坡度阻力；Fj为加速阻力。滚动阻力为：

其中：m为汽车质量；g为重力加速度；fr为滚动摩擦系数；ηr为传动效率；i0为主减速器传动比；ig为变速器传动比。空气阻力为：

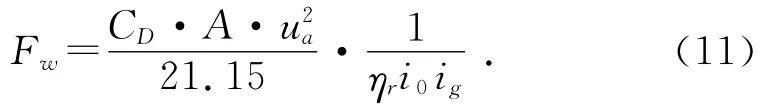
其中：CD为空气阻力系数；A为迎风面积；ua为汽车行驶速度。坡度阻力为：

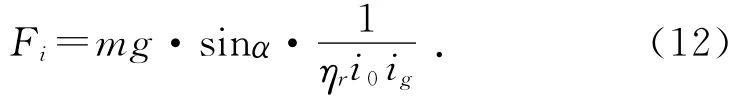
其中：α为坡度角。加速阻力为：

其中：δ为旋转质量系数，δ＝1.03。

速度表达式：

其中：n为电动机转速；r为电动汽车车轮半径。根据式（9）～式（14）得到的阻力，可以计算出汽车行驶时的阻力转矩：

把式（9）～式（14）代入式（15），得到如下方程：

根据汽车动力学数学模型，建立阻力转矩模型如图9所示，仿真条件是在平坦道路，4个阻力送到sum模块后，再通过Torque convertor转换为电机所受到的阻力转矩Tm。

图8 转速PI调节器

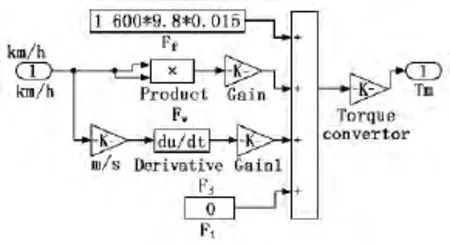
图9 阻力转矩模块

3 仿真及结果分析

三相异步感应电机参数为：额定功率30kW，额定电压200V，额定频率120Hz，额定转速3 600r/min，定子电阻R1＝0.435Ω，转子电阻R2＝0.816Ω，定子漏感Lr＝2mH，转子漏感Lr＝2mH，定转子互感Lm＝69.31mH，转子转动惯量J＝0.089kg·m2，极对数np＝2。

参数设置：磁通给定值0.96Wb，开环控制，PI控制器的比例常数Kp＝45，积分常数Ki＝35，给定转矩限定在300N·m，滞环宽度为18A。仿真算法采用ode15s算法。

（1）工况1：缩小的ECE循环工况如图10所示，在0s～0.5s为匀加速阶段，在0.5s～1s为匀速阶段，速度为2.5km/h，1s～1.5s为匀减速。仿真波形如图11、图12、图13所示。

图10 给定车速

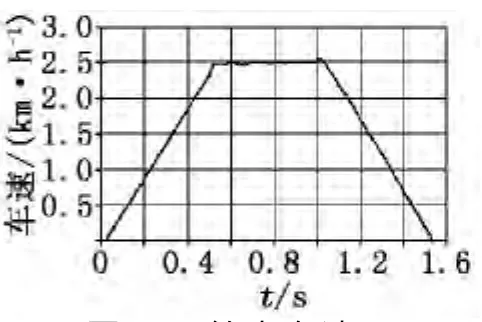
图11 输出车速

图12 输出转矩

图13 输出电流

（2）工况2：车速阶跃信号如图14所示，在0s时突然给定车速为2.5km/h，在0s～0.5s为匀速，在0.5s时又突然给定速度为0km/h，在0.5s～1.0s速度始终为0km/h。仿真结果如图15、图16、图17所示。

图14 输入阶跃车速

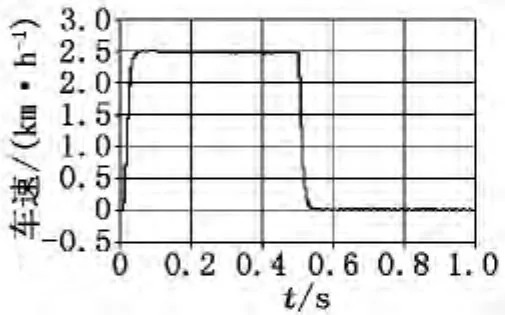
图15 车速阶跃响应

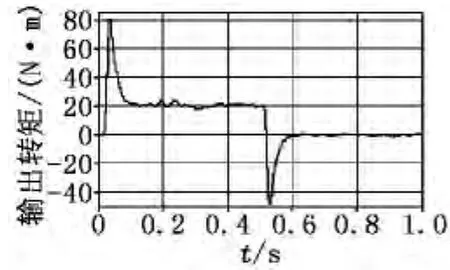
图16 电机输出转矩

图17 输出电流

以上两种工况的仿真结果表明：①电动汽车速度的输出值与给定值吻合得非常好；②感应电机的输出转矩满足电动汽车的动力性要求；③根据工况和车速的变化，电流输出响应迅速。仿真结果证明了本文提出的PID控制方案合理且有效。

4 结论

本文在矢量控制技术的基础上分析并提出了一种基于Simulink的电动汽车电机的PID控制方案，采用两种工况对其模型进行了仿真分析。结果表明：系统响应与理论分析一致，系统运行较好，并且具有良好的动态性能，能够满足各种复杂工况的要求。证明了本文提出的PID控制分析方案合理且有效。

［1］潘晓晟，郝世勇.MATLAB电机仿真精华50例［M］.北京：电子工业出版社，2007.

［2］胡虔生，胡敏强.电机学［M］.北京：中国电力出版社，2005.

［3］余志生.汽车理论［M］.第4版.北京：机械工业出版社，2008.

［4］陈杰.MATLAB宝典［M］.北京：电子工业出版社，2007.

［5］周松林，朱云国，贡照天.电动汽车用感应电动机矢量控制技术仿真实现［J］.自动化与仪器仪表，2007（6）：9-11.

［6］邵杰.基于Matlab/Simulink异步电机矢量控制系统仿真［J］.自动化技术与应用，2009，28（3）：73-76.