模糊环境下Stackelberg博弈的均衡利润分析
晋盛武, 丁浩然
(合肥工业大学 经济学院,安徽 合肥 230009)
0 引 言
博弈模型分析和考察了利益不尽相同的决策主体之间策略的相互影响及其均衡结果。文献[1]提出所有数据和参数都必须是确定值的模型,称为基于确定值的模型。斯坦克尔伯格(Stackelberg)模型就是市场上相互影响的厂商根据自己的利润函数,以产量作为策略独立进行决策,寻求利益最大化的经典确定值模型之一。然而在现实决策过程中,由于市场需求和厂商成本的波动导致信息不确定性的存在,或是由于人们对确定性因素的不确定性认知,限制了确定值模型的实用性,因此,有必要对不确定值情况下应用确定性的模型(如斯坦克尔伯格模型)进行拓展,以增加博弈论经典模型对现实问题的解释力。
文献[2]提出模糊集和模糊逻辑概念,为认识界限不甚分明的事物提供了有效的测度工具;文献[3]在每个参与者的计划都是线性模糊的基础上提出了模糊矩阵博弈;文献[4]在具有模糊报酬的双矩阵博弈下,定义了2种均衡策略的概念,并研究了它们之间的意义;文献[5]在需求为随机模糊变量的假设下,将经典报童问题拓展为基于随机模糊需求的自由分布报童模型。研究者利用加权质心的思想,将模糊转化为确定性估值进行研究:文献[6]利用质心思想将模糊数转化为确定性估值,拓展了需求和供给是模糊线性函数条件下,市场均衡时的消费者剩余和生产者剩余;文献[7]分析了模糊环境下的古诺模型,并利用三角模糊数求出了模糊环境下古诺模型中厂商的最优产量,同时分析了反需求函数和成本函数中的模糊参数对厂商利润的影响,利用加权质心思想将模糊利润和参数转化为确定值,分析了参数质心对厂商利润及利润变化幅度的影响。
本文在文献[7]的基础上,提出了模糊需求和模糊成本下的斯坦克尔伯格博弈的均衡求解方法和相应的均衡结果;采用文献[8]的加权质心WCoG方法,将每个厂商的模糊利润函数转化为确定性估值,每个厂商依据利润函数的最优解决策其产量,且在模糊均衡时都没有动机去改变均衡的结果;利用文献[9]的方差公式计算厂商模糊利润函数的方差。为了方便计算,假设每个厂商的需求函数和成本函数都是含有三角模糊参数的线性代数式。
1 模糊斯坦克尔伯格模型
假设市场上只有厂商1和厂商2,其中厂商1为领导者,厂商2为追随者。厂商i(i=1,2)的模糊利润记为,假设(Q)是模糊的逆需求函数,(qi)是厂商i的模糊成本函数,Q为双寡头厂商的总产量,即Q=q1+q2,则有:
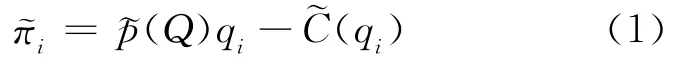
由于厂商i的利润表达的模糊性较难计算厂商的均衡解,本文以WCoG方法估计厂商的模糊利润[8],从而将模糊利润转化为确定性估值求解厂商的最优产量。
定义模糊利润函数的质心为:
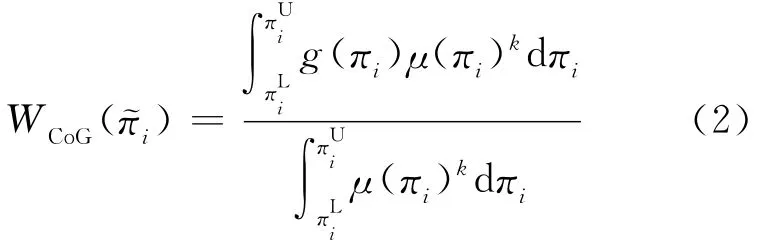
其中,g(πi)为考察对象πi的水平分量;μ(πi)为隶属函数值;k为控制参数,区间为[1,+∞)。
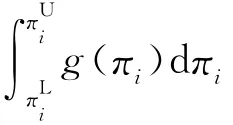
为简单起见,假设逆需求函数和成本函数都是线性的,所有的参数都是三角模糊数,并假设所有模糊数都是非负值,于是得到产品价格(Q)的三角模糊数为:

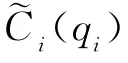
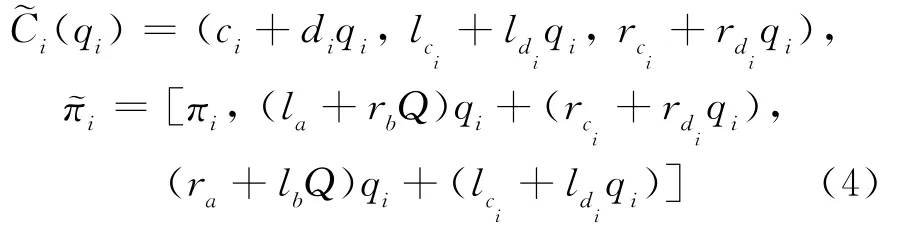
为了简化运算,假设k=1和g(x)=x。由于每个厂商的模糊利润函数都是三角模糊数,则WCoG()能简单地计算出来[8],即
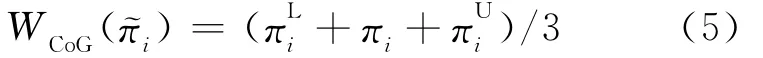
根据逆向归纳法求解博弈均衡,先假设厂商1的产量q1是确定的,则厂商2对模糊利润的估值WCoG)对q2的一阶导数为:

令(6)式等于0,则可求出厂商2利润最大化时的最优反应函数,即厂商2产量q2与厂商1产量q1之间的关系为:
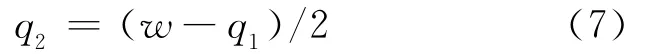
其中
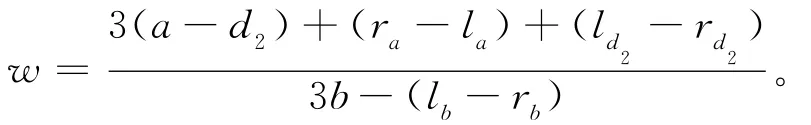
将(7)式带入厂商1的利润函数中,可得:

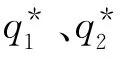
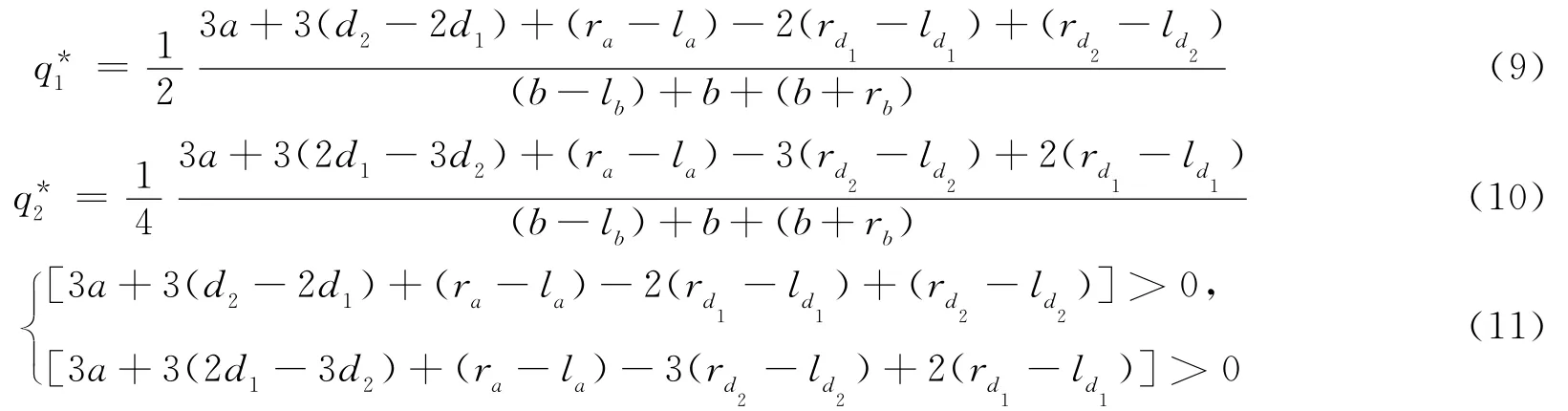
2 参数变动的灵敏性分析
灵敏性分析考察参数变动对模型均衡结果的影响,从(9)式、(10)式可以看出,对于厂商i,其均衡产量不仅与其模糊参数的确定值有关,还与参数的模糊范围有关。
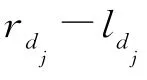
2.1 参数质心的影响
考虑三角模糊参数a的质心,可得:

其他模糊参数的质心为:
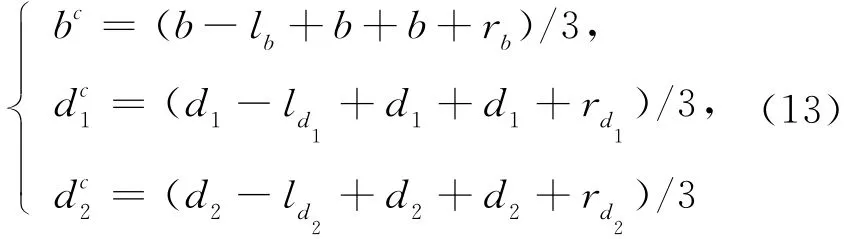
将(12)式、(13)式带入(9)式、(10)式,得到厂商的均衡产量为:

由(14)可以看出,厂商的均衡产量与模糊参数的质心ac、bc、和相关。厂商对市场需求函数的估计会影响均衡产量,模糊参数的质心ac越大,厂商的均衡产量越大,而模糊参数的质心bc越大,厂商的均衡产量越小;厂商边际成本的质心与自己的均衡产量成负向关系,与对方厂商的均衡产量成正向关系。并且,斯坦克尔伯格模型原有的先动优势在模糊环境下,其参数质心必须满足>0的条件才可成立,即厂商1的先动优势必须满足
由(14)式可得市场的总需求为:
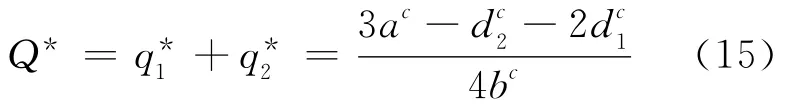
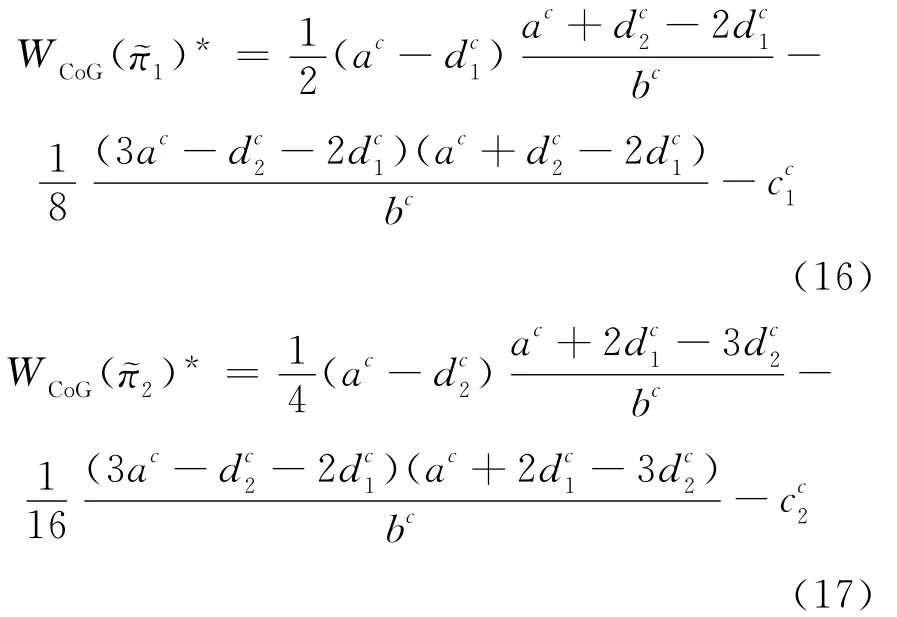
在模糊环境下,厂商的均衡产量、均衡总产量和2个厂商模糊利润的均衡质心对模糊参数质心的一阶导数结果,见表1所列。

表1 模糊环境下均衡结果对不同模糊参数质心的一阶导数
通过一阶导数考察参数模糊质心变化对均衡结果的影响。
(1)厂商i的均衡产量是ac和的增函数,是bc和的减函数;厂商1对市场容量参数质心和厂商2边际成本质心的反应,要弱于厂商2对市场容量参数质心和厂商1边际成本质心的反应,因此,厂商2更在意竞争市场容量的大小和厂商1的边际成本。
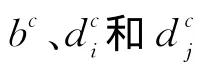
(3)厂商1的WCoG)是关于的增函数,关于bc的减函数。厂商2的是关于ac的增函数,关于的减函数。
在模糊环境下,古诺模型中市场需求、各个厂商的均衡产量及加权模糊利润对模糊参数质心一阶求导结果[6],见表2所列。
通过对比发现,在模糊环境下,参数ac对市场总需求Q、厂商i(i=1,2)的均衡产量qi及加权利润WCoG()都有正效应,而对于参数bc则都有负效应。厂商i的边际成本对市场总需求Q和竞争厂商j(j≠i)的均衡产量qj及加权利润WCoG()都有正效应,而对自身的均衡产量qi及加权利润WCoG)却有负面效应。

表2 模糊环境下Cournot模型中对不同模糊参数质心的一阶导数
2.2 模糊利润的方差分析
模糊利润的标准差[7]为:
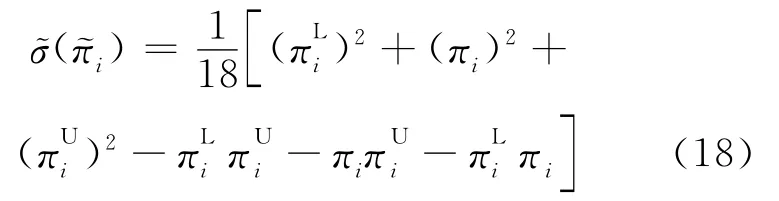
将(18)式对ac一阶求导,可得:
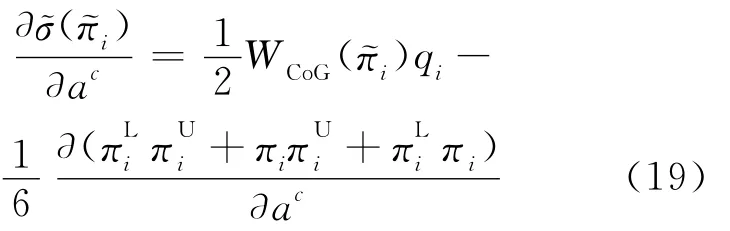
观察ac与()之间的关系,考虑(19)式右边第2个多项式,它能被分解为,对厂商1进一步简化,可得:
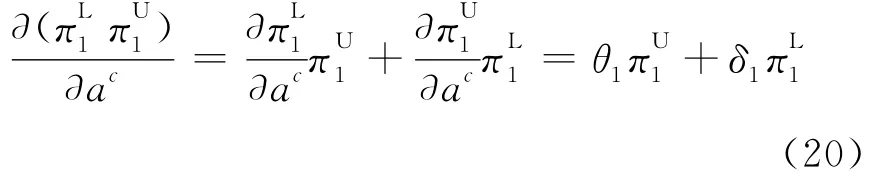
同理可得:


其中

将(20)~(22)式带入(19)式,可得:
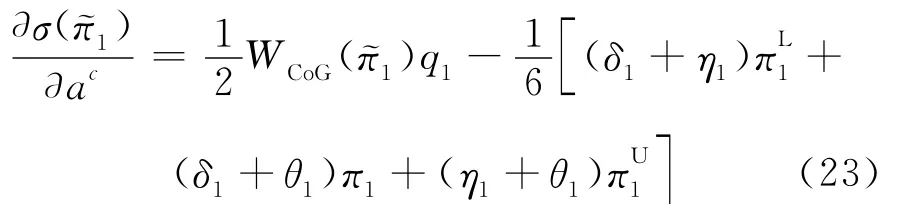
同样对于厂商2,可得:
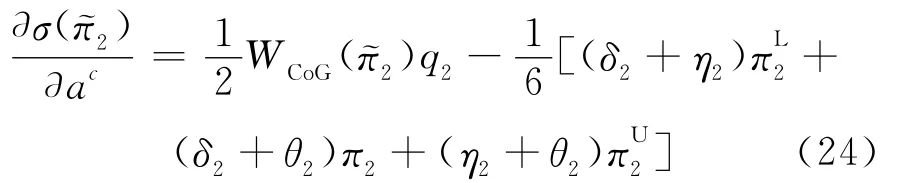
其中

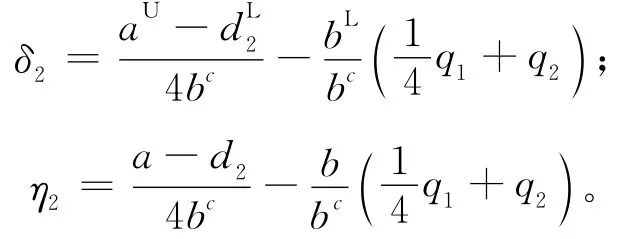
对于其他参数,分别对其一阶求导,可得:

其中
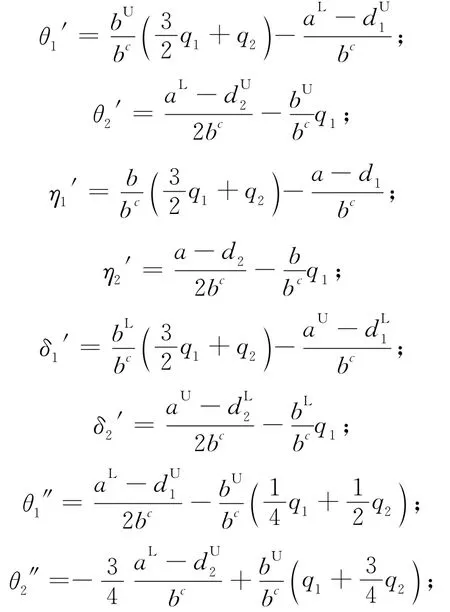
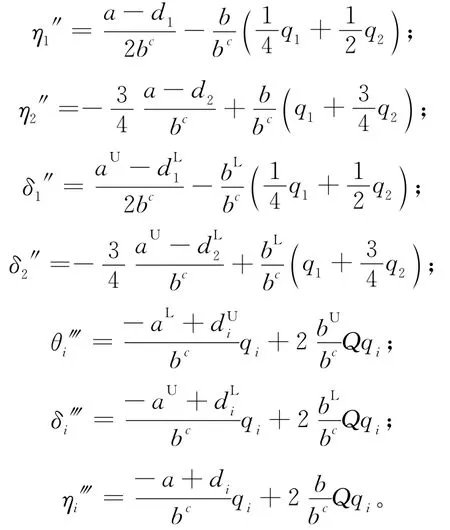
因此,(23)~(27)式表示模糊利润的标准差对于相应的模糊参数质心的变化率。不论是厂商1还是厂商2,其模糊利润的标准差是ac的增函数,即随着ac的增大,模糊利润的波动幅度会随之变大;而且都是bc的减函数,即随着参数bc的增大,模糊利润的波动幅度会随之变小。同时还可以发现,厂商1和厂商2的模糊利润标准差都是自身边际成本的减函数,是竞争对手边际成本的增函数。厂商自身的边际成本对自身模糊利润标准差的影响程度,大于竞争对手的边际成本的影响。
通过分析可知,在模糊环境下的斯坦克尔伯格模型中,逆需求函数和成本函数中的模糊参数对于均衡下每个厂商的均衡产量和均衡利润都有着重要的影响。
3 算例分析
通过厂商1和厂商2的最优产量比较,在模糊环境下,可以肯定厂商1的先动优势依然存在。
由参数质心公式,可以得到ac=10.5,bc=2.5=1.1,=1.3,并可以得到模糊环境下厂商的均衡产量、均衡总产量和2个厂商模糊利润的均衡质心对模糊参数质心的一阶导数的结果,见表3所列。
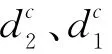
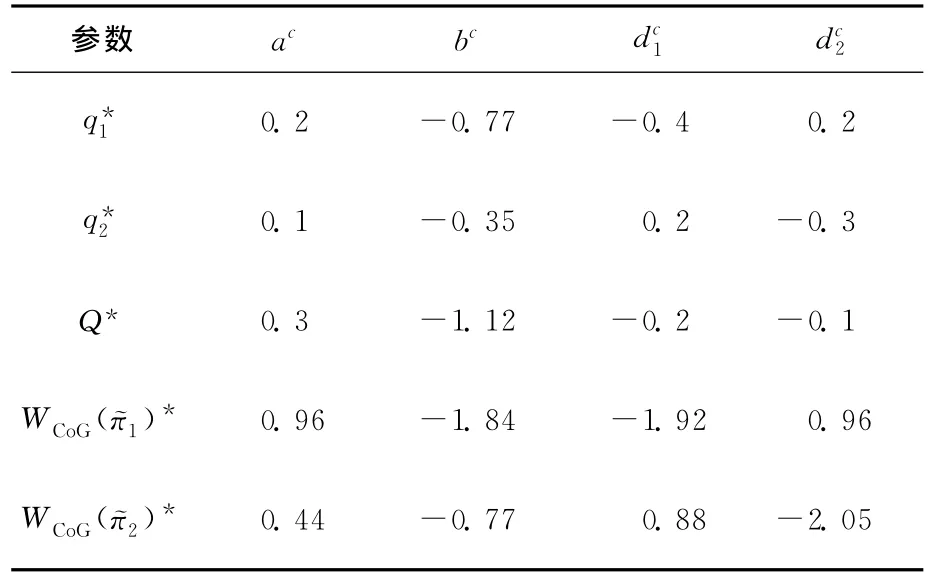
表3 对不同模糊参数质心的一阶导数结果
由厂商利润函数方差分析,可以得到每个厂商利润标准差对模糊参数质心的求导结果,即
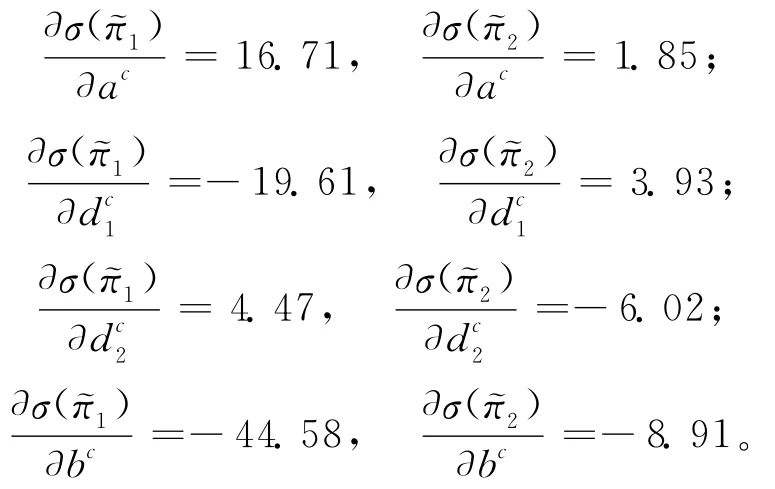
由结果可以发现,厂商1的利润标准差对模糊参数质心ac和bc比厂商2都更敏感,即ac和bc变动时,厂商1的模糊利润的变动幅度会更大。
4 结束语
本文在模糊环境下,求解需求和成本都不确定情况下的斯坦克尔伯格博弈均衡利润。为了计算方便,假设厂商需求和成本函数是含有模糊参数的线性函数。在设定模型中,可以得到厂商的均衡产量,进一步研究模糊利润的标准差,为决策者提供关于利润变化的更多消息。通过灵敏性分析,检验参数波动对每个厂商的均衡产量、模糊利润的加权质心以及总市场需求的影响,发现每个厂商的均衡产量对于本身参数的变动影响,大于其竞争对手参数的变动影响,其参数质心控制着模糊参数的变动影响均衡产量的波动。
[1] Liang G S,Lin Lingyuan,Liu C F.The optimum output quantity of a duopoly market under a fuzzy decision environment[J].Computers and Mathematics with Applications,2008,56:1176-1187.
[2] Zadeh L A.Fuzzy sets[J].Information and Control,1965(8):338-353.
[3] Campos L.Fuzzy linear programming models to solve fuzzy matrix games[J].Fuzzy Sets and Systems,1989,32:275-289.
[4] Maeda T.Characterization of the equilibrium strategy of the bimatrix game with fuzzy payoff[J].Journal of Mathematical Analysis and Application,2000:891-903.
[5] 赵 明,周永务.随机模糊需求下的自由分布报童问题研究[J].合肥工业大学学报:自然科学版,2011,34(6):931-934.
[6] Yao J S,Wu K.Consumer surplus and producer surplus for fuzzy demand and fuzzy supply[J].Fuzzy Sets and Systems,1999,103:421-426.
[7] Dang J F,Hong I H.The Cournot game under a fuzzy decision environment[J].Computers and Mathematics with Applications,2010,59:3099-3109.
[8] Bender M J,Simonovic S P.A fuzzy compromise approach to water resource systems planning under uncertainty[J].Fuzzy Sets and Systems,2000,115:35-44.
[9] Lee E S,Li R L.Comparison of fuzzy numbers based on the probability measure of fuzzy events[J].Computers and Mathematics with Applications,1988,15:887-896.

