自由度匹配技术在某贮箱结构模型修正中的应用
李伟明,时亚州,王 君,王 磊
(上海航天精密机械研究所,上海 201600)
0 引言
为掌握研究对象的动力学特性,需对其进行各种试验分析,而有限元分析则对试验分析有效的补充。但因有限元建模过程中不准确的模型简化以及材料、几何参数的不确定性等导致有限元模型的建模精度无法保证,使有限元模型的计算结果与试验的测试结果间存在较大差异,这就需要用模型修正技术修正结构的有限元模型,提高其精度及可靠性[1]。有限元模型修正中,模型自由度数常远大于试验测试的自由度数,由此产生了有限元模型自由度与试验测试模型不匹配,因此需在模型修正前对有限元模型与试验测试模型进行自由度匹配。自由度匹配有两种方法:一种是模型缩聚法,将有限元模型的自由度进行等效缩减,使之与试验测试模型自由度一一对应,缩聚后模型的保留自由度信息中包含被缩聚自由度的信息,模型缩聚可有效降低计算规模,提高计算效率;另一种是模态扩展方法,通过插值技术对试验测试获得的模态振型进行扩阶,使其自由度数等于有限元模型的自由度数[2-6]。目前,多数理论研究和实际应用集中在前者,算法也较成熟。模态扩展法虽然会增加一定的计算量,但在对试验模态插值过程中,可一定程度对试验模态数据进行降噪和平滑,有助于提高试验数据的精确性。
为获得高精度的某贮箱结构有限元模型,本文用ICMCM法对有限元模型修正进行了研究[7-8]。
1 改进的ICMCM
假定已通过某种自由度匹配技术完成了有限元模型与试验测试模型的自由度匹配过程。令有限元模型与试验测试模型间存在关系
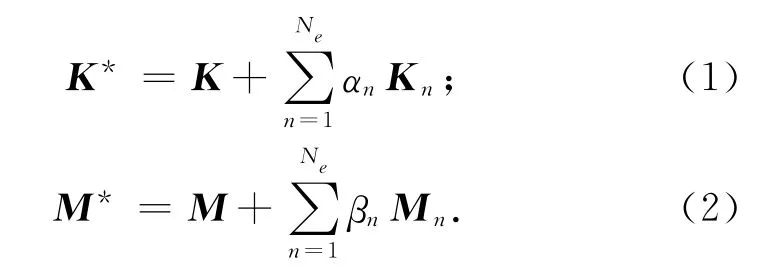
式中:K,M分别为有限元模型的刚度阵和质量阵;K*,M*分别为试验测试模型对应的刚度阵和质量阵;αn,βn为第n个有限元单元的刚度和质量修正因子;Ne为有限元单元数。
对无阻尼的自由振动系统,其有限元模型第i阶特征方程为
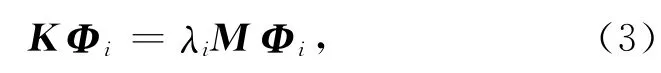
同样,设试验测试模型为无阻尼的自由振动系统,其第j阶特征方程为
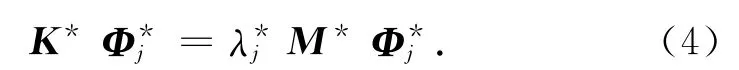
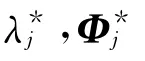
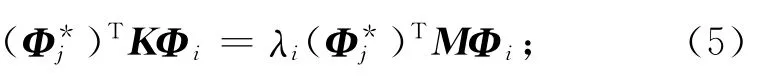
式(4)左乘(Φi)T得

考虑()TKΦi为一标量,同时利用到刚度阵与质量阵的对称性,则有
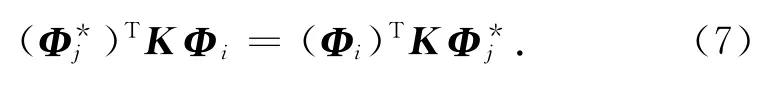
类似可有

将式(7)、(8)代入式(5)得

式(6)减去式(9)得
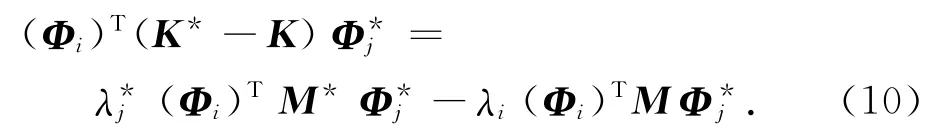
将式(1)、(2)代入式(10),整理后有
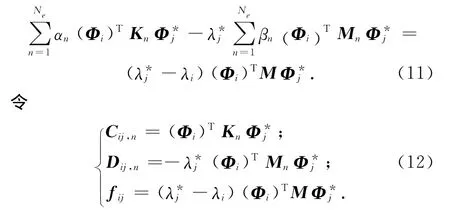
将式(12)代入式(11)得
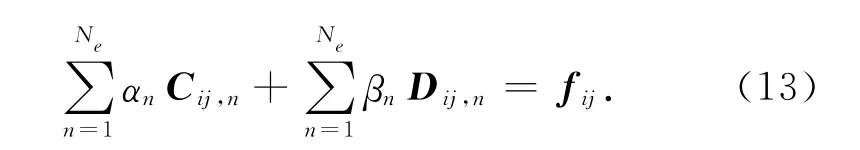
求解式(13),得到参数的修正量αn,βn后,参考式(1)、(2)即可获得修正后的参数。
2 某贮箱有限元模型修正
用MSC.Patran软件建立某贮箱结构有限元模型如图1所示。建模后,模型共有梁单元32个,板单元404个,节点389个,自由度总数2 334。该贮箱结构较复杂,内部有两层加筋梁,在结构连接部位存在大量的焊接及铆接部位,导致有限元建模的计算结果与试验对象的测试结果间存在较大误差,初始有限元模型建模精度不高,对此需用有限元模型修正技术对初始有限元模型进行修正,提高模型的可靠性。为模拟试验测试对象的状态,需对仿真试验模型的参数添加随机扰动,其中对模型中存在较大误差的5组连接部位及其附近单元参数添加较大扰动。这5组连接部位如图2所示。
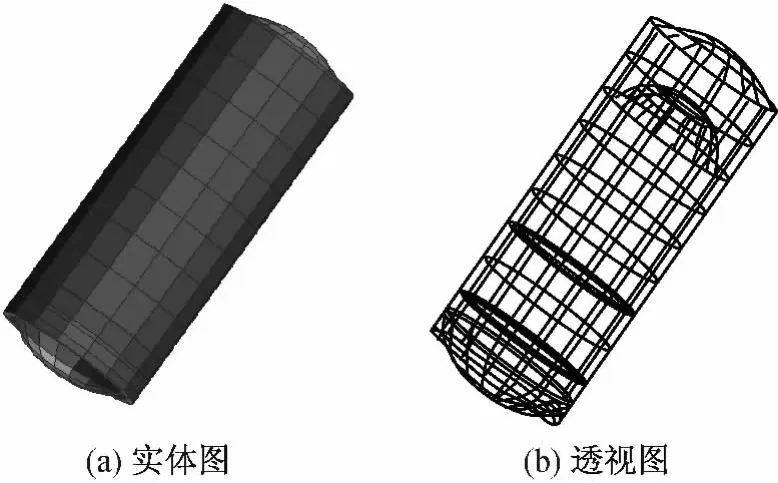
图1 某贮箱结构模型Fig.1 Model of a cabin structure
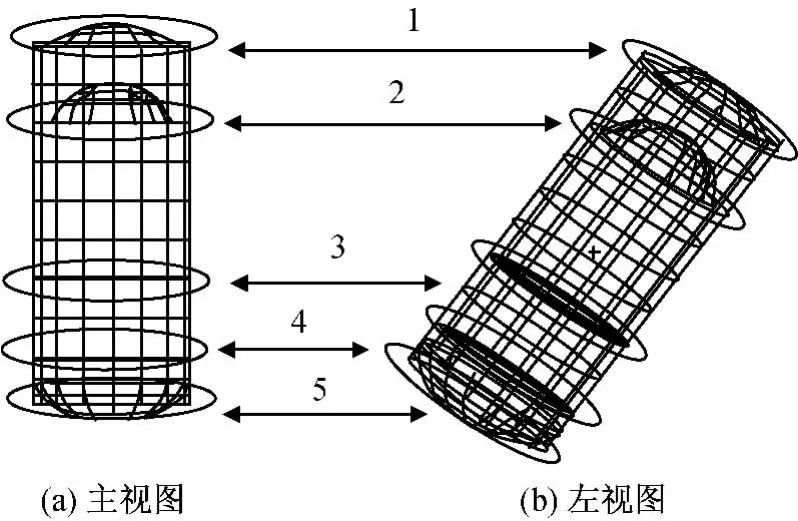
图2 存在较大误差的连接部位Fig.2 Connection parts with large modeling errors
仿真试验模型生成后,提取模型的频率及模态振型作为仿真试验数据。因真实试验数据不可避免会受测试噪声的影响,为模拟噪声干扰下的试验数据,需对仿真试验添加噪声:频率添加3%的噪声;模态振型添加7%的噪声[9]。修正前,有限元模型与仿真试验模型的频率以及模态置信准则(MAC)的关系分别见表1、2。
与仿真试验数据进行对比,修正前初始有限元模型的前9阶频率误差均已超过10%,MAC值对角线的第4,7个元素均小于0.4,有限元模型与仿真试验模型的振型误差极大,需进行有限元模型修正提高初始模型的可靠性。
在真实试验测试中常只能测得少量低阶的模态频率及模态振型,故假设仿真试验中仅能测量得到试验的前9阶模态。根据国际通用的有限元模型修正评价准则,修正时仅用1~6阶模态频率及其对应的模态振型,7~9阶不参与修正过程,用于验证模型修正的效果[10]。
因该贮箱模型结构较大且复杂,设仅沿舱体自上而下的节点16,18,21,47,82,90,100,122,127,140,142,162,174,184,196,199,204,339的x,y,z三个方向的自由度可测,则测量自由度数为54,为有限元模型自由度总数2 334的2.31%。模型修正前,先对有限元模型与仿真试验模型进行自由度匹配,使两者能在相同自由度下进行修正。本文用ICMCM法分别配合使用模型缩聚法与模态扩展法对贮箱进行修正。修正对象选定为所有436个单元的杨氏模量,修正时添加5组连接部位及其附近单元杨氏模量相等的12个约束方程,最终修正参数为192个。修正过程中用约束最小二乘法求解修正公式[11]。
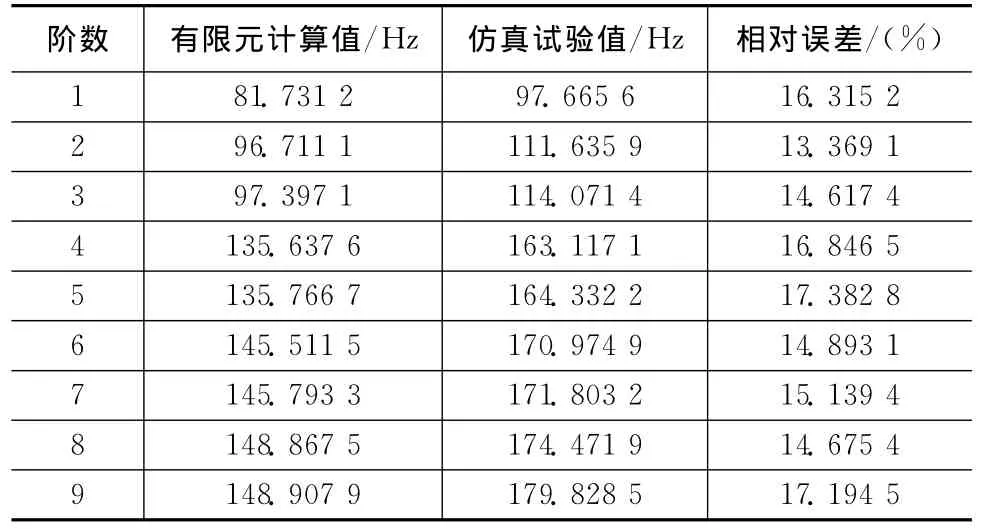
表1 修正前频率比较Tab.1 Frequency comparison between initial finite element model and test data
2.1 采用模型缩聚的修正结果
此处使用4级逐级近似模型缩聚方法对有限元模型进行缩聚,缩聚后有限元模型的自由度数为54,修正过程中使用缩聚后有限元模型全部的54阶模态数据以及仿真试验的前6阶模态数据,这样共生成324个修正方程[2]。

表2 修正前MAC值比较Tab.2 MAC comparison between initial finite element model and test data
用上述数据对贮箱进行修正,结果见表3、4。因待修正参数数量较大而修正方程的个数相对较少,修正结果并不理想。表3中使用的前6阶频率和用于校核模型修正效果的7~9阶频率较初始状态均未好转,而修正后的MAC值较初始状态几乎未发生改变。

表3 ICMCM法及模型缩聚修正的频率Tab.3 Frequency using ICMCM method and model reduction
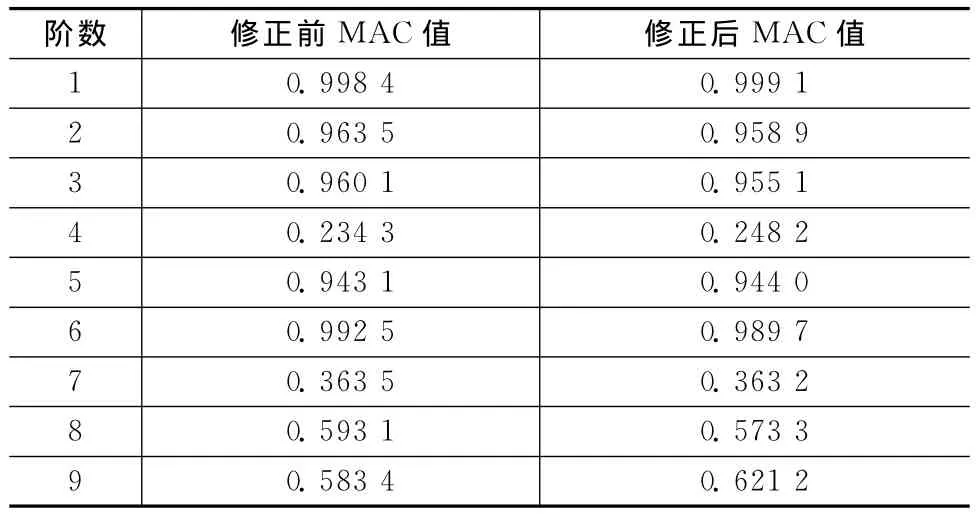
表4 用ICMCM法及模型缩聚修正的MACTab.4 MAC using ICMCM method and model reduction
2.2 采用模态扩展的修正结果
用传统的模态扩展法,即直接使用有限元模型的模态振型数据补足试验模型的模态振型,修正过程中有限元模型的试验模型的自由度均为2 334。修正过程中仅使用有限元模型的前100阶模态数据和仿真试验的前6阶模态数据,共生成方程600个。
修正后有限元模型与仿真试验模型的频率见表5。由表可知:虽存在测试噪声的干扰,修正后有限元模型的频率值更逼近仿真试验值,修正时所用的前6阶频率的最大误差由17.382 8%变为1.935 3%,平均误差由15.570 7%变为1.023 2%;7~9阶频率的最大误差由17.194 5%变为2.477 2%,平均误差由15.669 7%变为0.989 5%。
ICMCM法及模态扩展修正的MAC见表6。由表可知:修正后前6阶模态MAC值对角线元素的最小值由0.234 3变为0.993 3,平均值由0.848 76变为0.997 2;7~9阶模态MAC值对角线元素最小值由0.363 5 变 为 0.854 7,平 均 值 由 0.513 3 变 为0.883 2。其中修正前有限元模型第4阶模态及第7~9阶模态对应的MAC值均小于0.6,修正后这些阶模态对应的MAC值均已大于0.85。
上述模型修正结果表明:对待修正参数众多的模型修正问题,ICMCM法更适于结合模态扩展方法进行应用。其中主要原因是在贮箱模型修正过程中选择了192个参数进行了修正,用模型缩聚后模型修正时,因模型缩聚使有限元模型规模变小,导致可供修正使用的有限元模型信息较少,故生成的修正方程数量有限,另外模型缩聚是一种近似方法,缩聚后的有限元模型不能完全反映缩聚前模型的动力学特性,尤其是在试验数据受到噪声干扰时,求解含待修正参数较多的修正方程的结果有时不理想;用模态扩展方法进行修正时,因扩展后可供使用的模型信息较多,可生成的修正方程数量较多,故能用于求解数量较多的待修正参数。
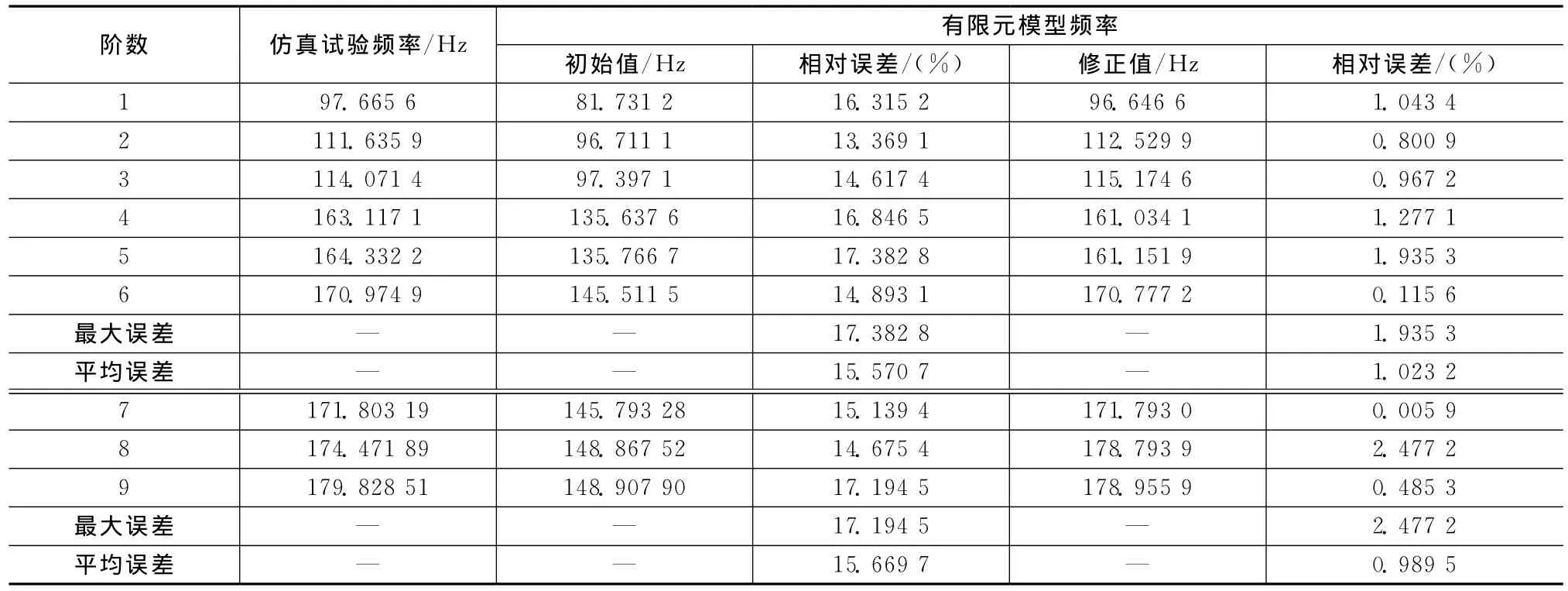
表5 ICMCM法及模态扩展修正的频率Tab.5 Frequency using ICMCM method and modal expansion
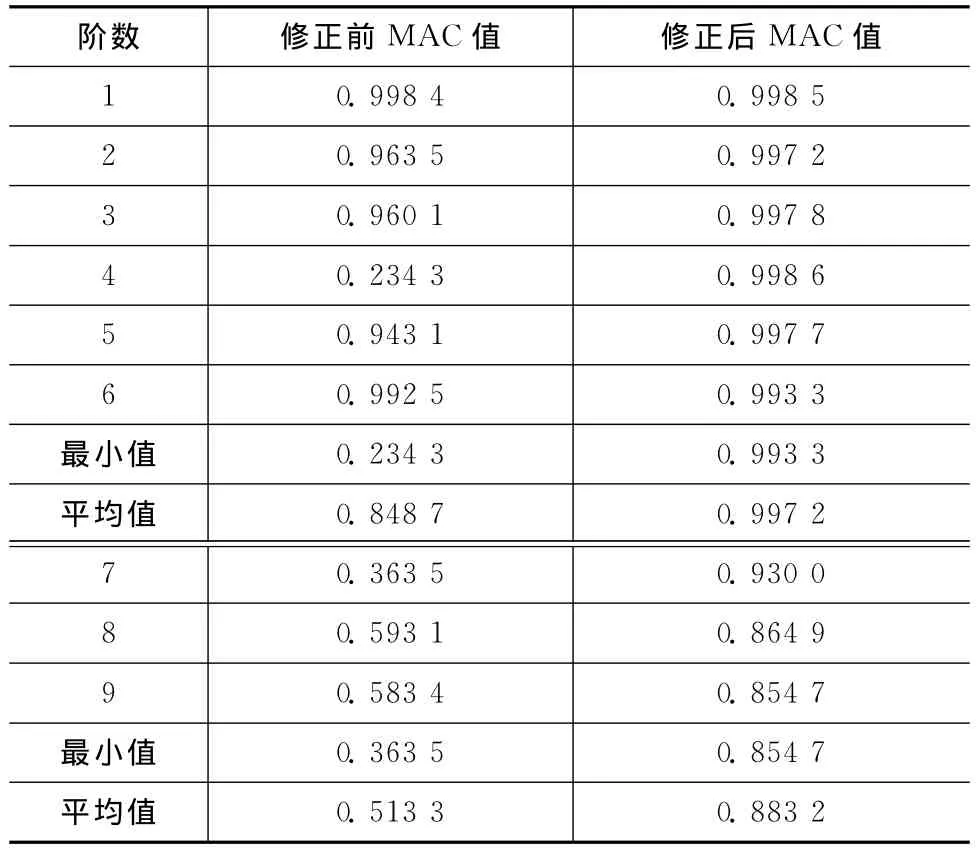
表6 ICMCM法及模态扩展修正的MACTab.6 MAC using ICMCM method and modal expansion
3 结束语
本文对某贮箱模型的修正进行了研究,分别用模型缩聚和模态扩展方法与ICMCM法配合使用对贮箱进行修正。该法无需进行灵敏度分析并有较好的误差判断能力,提高了修正后模型的可靠性,且计算效率高,可同时修正大量参数。因修正时可供使用的仿真试验数据较多,用模态扩展方式进行修正获得了理想的模型修正结果,在修正时所用的频段和用于校核修正结果的频段内,模态频率与MAC值的误差均较初始状态有明显改进。修正结果表明:在对修正参数较多的结构进行模型修正时,若不考虑修正计算时间,建议使用模态扩展方法结合ICMCM法。本文研究证明ICMCM法可同时修正大量待修正参数,有较高修正精度。
[1] MOTTERSHEAD J E,FRISWELL M I.Model updating in structural dynamics:a survey[J].Journal of Sound and Vibration,1993,167(2):347-375.
[2] ZHANG D W,LI J.Succession-level approximate reduction(SAR)technique for structural dynamic model[C]//Proceedings of 7th International Modal Analysis Conference.Las Vegas:[s.n.],1989:29-37.
[3] 朱安文,曲广吉,高耀南.航天器结构动力模型修正中的缩聚方法[J].中国空间科学技术,2003,23(2):6-10.
[4] O'Callahan J.An efficient method of determining rotational degrees of freedom from analytical and experimental model data[C]//Proceedings of 4th International Modal Analysis Conference.Las Vegas:1986:50-58.
[5] 汪晓红,周传荣,徐庆华.结构分析模型的修正与振型扩充技术[J].东南大学学报(自然科学版),2000,30(2):143-147.
[6] 秦仙蓉,张令弥,顾 明,等.改进的基于模态参数的结构计算模型修正算法[J].同济大学学报,2002,30(11):1295-1299.
[7] HU S L J,WANG S Q,LI H J.Cross-modal strain energy method for estimating damage severity[J].Journal of Engineering Mechanics,2006,132(4):429-437.
[8] 王金明,李伟明,彭明峰.基于ICMCM法的GARTEUR结构有限元模型修正研究[J].振动与冲击,2011,30(5):90-95.
[9] 杨海峰.基于加速度频响函数的结构损伤检测方法研究[D].西安:西北工业大学,2007.
[10] LINK M,FRISWELL M I.Working group 1:Generation of validated structural dynamic models-results of a benchmark study utilising the GARTEUR SMAG19test-bed[J].Mechanical Systems and Signal Processing,2003,17(1):9-20.
[11] 桂 冰,戴 华.结构计算模型修正的二次约束最小二乘算法[J].振动与冲击,2006,25(2):41-43.

