远程导引脉冲变轨方案的有限推力修正

赵春慧，李仕海

（上海宇航系统工程研究所，上海 201109）

0 引言

国内外对远程导引变轨方案设计进行了大量研究。文献［1，2］介绍了远程导引段的Hohmann交会、双椭圆转移和Lambert交会等方法；文献［3］在考虑测控约束的条件下，针对燃料消耗最优、交会时间最优或两者加权最优的目标进行了多脉冲变轨设计。上述脉冲式变轨是工程问题的简化处理。实际变轨过程中，推力大小有限，推进并非瞬时进行，特别是容许过载较小的卫星进行大轨道转移时，在轨道上存在较长的推力弧段，此时脉冲假设不再成立。随着高性能，中、低推进水平的液体火箭发动机的广泛采用，对有限推力变轨进行了大量研究［4－6］。但与脉冲变轨相比，有限推力变轨设计的理论研究和工程实践尚不成熟。另外，设计对远程导引变轨方案时，摄动模型一般较简单（至多粗略估计J2项的长期效应），当飞行时间较长时摄动模型误差对交会结果的影响的积累量较大，会使由设计获得的变轨方案在实际摄动模型中难以实现追踪航天器和目标航天器的拦截或交会。

为此，本文对多脉冲式变轨方案的转换修正算法进行了研究。

1 基本原理

1.1 转换原理

脉冲式变轨方案到有限推力式变轨方案的转换如图1所示。图中：第i次速度脉冲Δvi作用在变轨时刻ti，第i次推力矢量Fi作用开始和结束时刻分别为tbi，tfi，1≤i≤n。

图1 脉冲式变轨到有限推力式变轨

由牛顿第二定律，Fi的作用时间

式中：M为变轨过程中航天器的平均质量；F为发动机推力。F为常值时，式（1）可近似变为

此处：ω为有效排气速度。

在确定Fi作用的开始和结束时刻后，还应确定其在作用时间内的推力方向，可用轨道系中的方位角Al和俯仰角Ei描述，即

式中：Δvix，Δviy，Δviz分别为 Δvi在轨道系x、y、z三轴的分量；Δvi＝｜Δvi｜。

发动机在工作过程中，其推力方向分为惯性系定向和轨道系（原点在航天器质心，z轴垂直向下指向地心；x轴在轨道平面内，垂直于z轴，指向前；y轴垂直于轨道平面，指向右）定向两种。惯性系定向是指在发动机点火时刻将推力方向调至Ai，Ei，此后推力方向在惯性空间保持不变；轨道系定向是指在整个发动机工作时段内不断调整推力方向，使之在轨道系中的方位角、俯仰角始终为Ai，Ei。工程中惯性系定向更易实现，轨道系定向可在固定方位、俯仰偏置角的准对地定向三轴稳定模式下操纵，或采用摆动发动机在对地定向三轴稳定模式下操纵。

1.2 修正原理

记远程导引结束时刻tf时追踪航天器和目标航天器的相对位置和相对速度矢量分别为ΔRf，Δvf，则实现交会的条件为

实现拦截的条件为

此修正问题实际是求解无约束优化问题

式中：X为优化变量（可选择历次变轨的起始、结束时间、推力方位角、俯仰角等变量）。

ΔRf，Δvf各有三个分量，当且仅当优化变量个数≥6时，交会问题可解；当且仅当优化变量个数≥3时，拦截问题可解。

一般，由初始脉冲式变轨方案转换得到的有限推力式变轨方案为此优化问题提供了一组较好的初值。只要选择合适的优化算法并构造合适的优化变量和目标函数，此优化问题能快速收敛至最优解。

1.3 算法流程

算法流程如图2所示。其中：修正算法模块为核心部分，包括优化算法模块和预报器模块两部分。

L－BFGS－B算法依赖于模型梯度信息，可求解精确的局部最优解，对初值依赖性较强［7］。遗传算法不依赖于模型梯度信息，使用随机转换原则工作，可将结果优化至全局最优解附近，对初值依赖性弱［5］。当优化问题初值较好时，可直接用L－BFGSB算法求解；当初值不好时，可先用遗传算法将结果优化至全局最优解附近，再用L－BFGS－B算法求取精确的全局最优解。

遗传算法设计流程包含参数编码、初始群体的设定、适应度函数的设计、遗传操作设计和控制参数设定五个基本要素。其中，参数编码将需优化的参数结合入遗传算法，主要有二进制编码、浮点数编码、动态变量编码等方式。本文问题为多约束多目标连续变量优化问题，故采用浮点数编码。

图2 修正算法流程Fig.2 Modified algorithm flowchart

控制参数选择对遗传算法收敛的作用非常重要。本文通过对交叉概率和变异概率的控制，使遗传算法达到自适应控制，在算法的速度和寻优能力间取得了较好平衡。

STK／Astrogator预报器是STK软件中的轨道机动模块，此模块（通过STK／X技术嵌入程序）能提供真实摄动环境中的精确轨道数据，但存在仿真速度慢的问题；J234轨道预报器是指在无推力作用段和推力作用段分别采用J234解析轨道预报器和Cowell数值积分法进行轨道预报，一般情况下其精度能满足要求，具有仿真速度快的优点。

2 优化问题分析

空间轨迹优化是多变量复杂问题，非线性程度高，收敛性与初值误差、优化变量和目标函数选取关系密切。

2.1 初值误差分析

初值误差为转换误差和摄动模型误差。

不同工况下由脉冲转换为有限推力后的位置误差如图3所示。图中：实线表示轨道系定向；虚线表示惯性系定向。由图可知：脉冲速度越小，发动机的推力和卫星初始质量之比越大，转换误差越小；推力方向在轨道系定向的转换误差小于在惯性系定向的误差。

图3 不同工况下转换位置误差Fig.3 Transfer position error under various states

对摄动误差，其主要影响因素是地球非球形引力势。一般飞行时间越长，轨道高度越低，由摄动模型带来的误差就越大。

初始设计的多脉冲式变轨方案，转换为有限推力式后，在真实摄动环境中仿真，交会误差可达102～103km量级。

2.2 优化变量选择

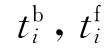
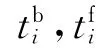
2.3 目标函数选择

对拦截，可直接将ΔRf作为目标函数，即

式中：Δx，Δy，Δz为拦截时刻两航天器在惯性坐标系或轨道坐标系中相对位置的三轴分量。

对交会，若用ΔRf，Δvf构造目标函数，则因两者量纲和量级均不同，目标函数相对优化变量的敏度较大，优化变量的微小变化就会引起目标函数值的剧烈振荡，目标函数随优化变量变化的曲线形态较恶劣，不利于优化问题的快速搜索求解。用相对轨道要素构造目标函数，可解决此问题［3］。

定义相对轨道要素型的目标函数

式中：D，Δex，Δey，Δix，Δiy，ΔM′为交会时刻两航天器的相对轨道要素；at0为初始时刻目标航天器的半长轴；Tt0为初始时刻目标航天器的轨道周期［8］。

相对轨道要素的定义如图4所示。图中：S0为基准航天器轨道；S1为伴随航天器轨道；O－XnYnZn为基准航天器节点坐标系Sn。

图4 相对轨道要素定义Fig.4 Definition of relative orbit elements

在摄动条件下，瞬时轨道要素时刻在变化，而平均轨道要素则是一组变化很慢的量。同理，为使目标函数随优化变量变化的曲线性态更平缓，更利于优化问题的快速求解，目标函数中所用的相对轨道要素采用交会时刻两航天器的平均轨道要素求得。

3 算例与分析

设初始时刻追踪航天器和目标航天器的轨道参数见表1。表中：a为半长轴；e为偏心率；i为轨道倾角；Ω为升交点赤经；ω为近地点幅角；f为真近点角。令追踪航天器的初始质量（包括燃料）1 000kg，变轨发动机推力50N，比冲300s。工程任务要求：将初始设计的脉冲式变轨方案转换为有限推力式并进行修正，使交会时刻两航天器的相对距离在15km以内，以便顺利转入近程阶段。

表1 初始瞬时轨道根数Tab.1 Initial instance orbit elements

将初始设计得到的4次脉冲式变轨方案转换为有限推力变轨方案，结果见表2。

表2 转换后的有限推力变轨方案Tab.2 Finite thrust orbital transfer after transition

采用转换后的有限推力变轨方案，真实飞行环境中，远程导引结束时刻两航天器的交会误差为176.74km（推力方向轨道系定向）；796.08km（推力方向惯性系定向）。两种定向的优化收敛过程分别如图5、6所示。

图5 推力方向轨道系定向修正收敛Fig.5 Modified convergence with orbit system orientation in thrust direction

图6 推力方向惯性系定向修正收敛Fig.6 Modified convergence with inertial system orientation in thrust direction

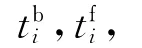
初始设计脉冲式变轨方案和不同修正结果的有限推力式变轨方案的燃料消耗为：脉冲式变轨方案37.117kg；推力方向轨道系定向（修推力方向）38.285kg；推力方向轨道系定向（不修推力方向）38.455kg；推力方向惯性系定向（修推力方向）40.424kg；推力方向惯性系定向（不修推力方向）49.309kg。

实际上，脉冲式变轨方案只是一种简化处理，实际工程中需转化为有限推力方案实施。用本文的方法进行转化和修正，由上述不同方案结果可知：有限推力式变轨方案消耗的燃料多于脉冲式变轨方案，这是因为在变轨弧段过程中存在引力损失；推力方向在惯性系定向消耗的燃料多于轨道系定向，是因为惯性系定向的引力损失大于轨道系定向；不修正推力方向的燃料消耗多于修正推力方向，是因为通过修正推力方向可通过寻优找到此种推力定向方式下（轨道系或惯性系中）引力损失最小要求的推力方位角和俯仰角。

4 结束语

本文对远程导引脉冲变轨方案的有限推力修正进行了研究，可基于真实飞行环境对变轨方案进行修正，仿真算例证明了各种工况下算法的有效性。由仿真结果可知：虽然推力方向在惯性系中定向较轨道系中定向操纵更容易，但消耗燃料更多。修正过程中可通过优化推力方位角、俯仰角，实现节省燃料目的。

［1］ 肖业伦.航天器飞行动力学原理［M］.北京：宇航出版社，1995：89－94.

［2］ BATE R R.航天动力学基础［M］.吴鹤鸣，李肇杰（译）.北京：北京航空航天大学出版社，1990：201－246.

［3］ 石 俊.航天器快速轨道机动策略规划研究［D］.北京：北京航空航天大学，2007.

［4］ LAWDEN D F.Optimal trajectories for space navigation［M］.London：Butter Worths，1963.

［5］ 汤一华，陈士橹，徐 敏，等.基于遗传算法的有限推力轨道拦截优化研究［J］.西北工业大学学报，2005，23（5）：671－675.

［6］ 王小军，吴德隆，余梦伦.最少燃料消耗的固定推力共面轨道变轨研究［J］.宇航学报，1995，16（4）：9－15.

［7］ BYRD R H，LU P，NOCEDAL J，etal.A limited memory algorithm for bound constrained optimization［J］.SIAM Journal on Scientificand Statistical Computing，1995，16（5）：1190－1208.

［9］ 杨 宇，韩 潮.编队飞行卫星群描述及摄动分析［J］.中国空间科学技术，2002，22（2）：15－23.