信息不确定下空战威胁评估方法研究

冯琦，张才坤，赵鸿森，陈军

(1.西北工业大学电子信息学院，陕西 西安710129;2.中国飞行试验研究院 航电所，陕西 西安710089)

0 引言

随着飞机隐身性能不断提高及干扰因素的增加，导致获取到的信息不确定性也不断增加［1］。但目前的评估方法［2-3］通常都以获取到准确目标信息为前提，很难处理由测量误差及复杂空战环境造成的不确定目标属性信息，因此非常有必要开展信息不确定下的空战威胁评估方法研究。

与其他描述手段相比，区间值直觉模糊集［4］(Interval Valued Intuitionistic Fuzzy Sets，IVIFS)适宜于处理包含不确定性因素问题。本文尝试将IVIFS引入到空战多目标威胁评估中，主要针对目标属性测量误差及目标机动或环境干扰引发的不确定性展开研究，通过IVIFS理论确定目标属性决策矩阵。考虑到空战威胁评估是在有限数据信息的背景下评估的，将交叉熵(Cross Entropy，CE)［5-6］原理运用到IVIFS中，通过区间直觉模糊交叉熵(IVIFCE)确定目标属性权重。根据IVIFS加权集结算子［7］和得分函数［8］，求解各目标威胁评估排序，并通过实例验证了该方法的科学性和合理性。

1 区间值直觉模糊集

定义IVIFS:设非空论域X。在X上给定2个区间值映射 μA:X→I［0，1］和 νA:X→I［0，1］(I［0，1］为单位区间［0，1］)。若满足条件0≤sup{μA(x)}+sup{νA(x)}≤1，称μA和νA确定了论域X上的1个区间值直觉模糊集A，记为:

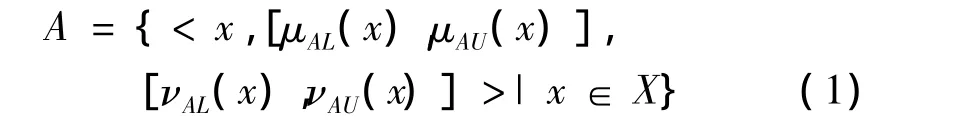
式中:［μAL(x)，μAU(x)］和［νAL(x)，νAU(x)］分别为A的区间隶属函数和区间非隶属函数;μAL(x)∈［0，1］;μAU(x)∈［0，1］;νAL(x)∈［0，1］;νAU(x)∈［0，1］;μAU(x)+νAU(x)≤1。简记为:

对于论域 X上的区间值直觉模糊集 A，称πA(x)=［1 － μAU(x)－ νAU(x)，1 － μAL(x)－ νAL(x)］为A中元素x的区间犹豫度。

2 目标属性决策矩阵的确定

设空战中我机遭遇m架敌机，每架敌机具有n个属性。图1为我机与第i架敌机的空战态势。图中:S为我机;G为敌机;ri为双方距离威胁;qB+qR为角度威胁;vi为速度威胁。

选取目标空战能力、速度、角度和距离作为空战威胁评估的目标属性。实际中获取的这些属性值都存在不确定性。其原因一方面是由探测设备误差造成的，另一方面源于飞机的隐身性、电磁对抗等环境因素干扰。为保证威胁评估结果符合实际情况，对这些不确定性因素进行分析处理，即将测量的目标属性值转化为IVIFS值，从而构成目标属性决策矩阵。

2.1 空战能力威胁属性

空战能力包括机动性能、武器装备能力、电子对抗和隐身能力等。通过IVIFS语言变量对空战能力属性进行描述，如表1所示。

表1 IVIFS与语言变量对应关系Table 1 Corresponding relation between language variables and IVIFS

2.2 速度威胁属性

速度威胁是相对于我机速度而言的。相对我机的速度较大，则威胁度较大;相反，则威胁度较小。实际速度测量误差如图2所示。

图2 速度误差图Fig.2 Picture of speed error

图2 中的g点代表机载设备固有误差，速度测量误差计算公式为:

式中:y为速度测量误差;x为目标的实际速度;θ1，θ2为系数(θ1≥0，θ2≥0，θ3≥0)。

若测量第i个目标速度为xVi，则目标速度范围为［xVi－ yi，xVi+yi］。设我机速度为 xz，测量误差为δz，则我机的实际速度范围为［xz－ δz，xz+ δz］。那么目标相对我机速度大小的范围为［xVi－yi－xz－δz，xVi+yi－xz+δz］。速度威胁属性的区间隶属度与区间非隶属度计算公式分别为:

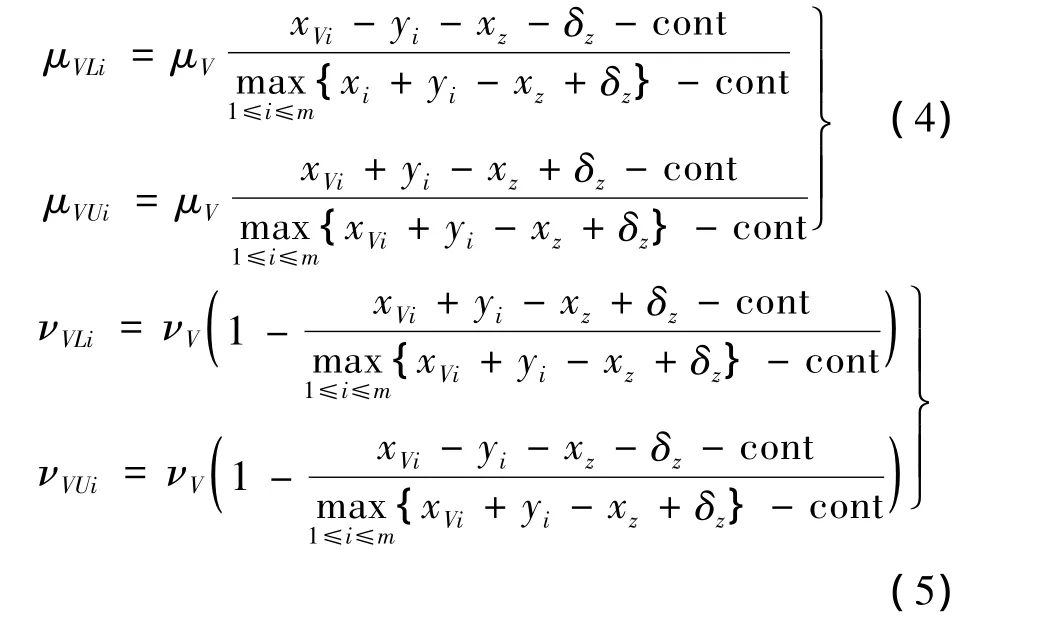
2.3 角度威胁属性

由图1可知，测量的角度为qR与qB角度之和。角度越小，威胁度越大;反之，威胁度越小。实际角度测量误差基本上在一定的区间内波动。因此，若测得与第i个目标的角度为xqi，则实际的角度范围为［xqi－δq，xqi+δq］，δq为角度测量误差。角度威胁属性的区间隶属度与区间非隶属度计算公式为:

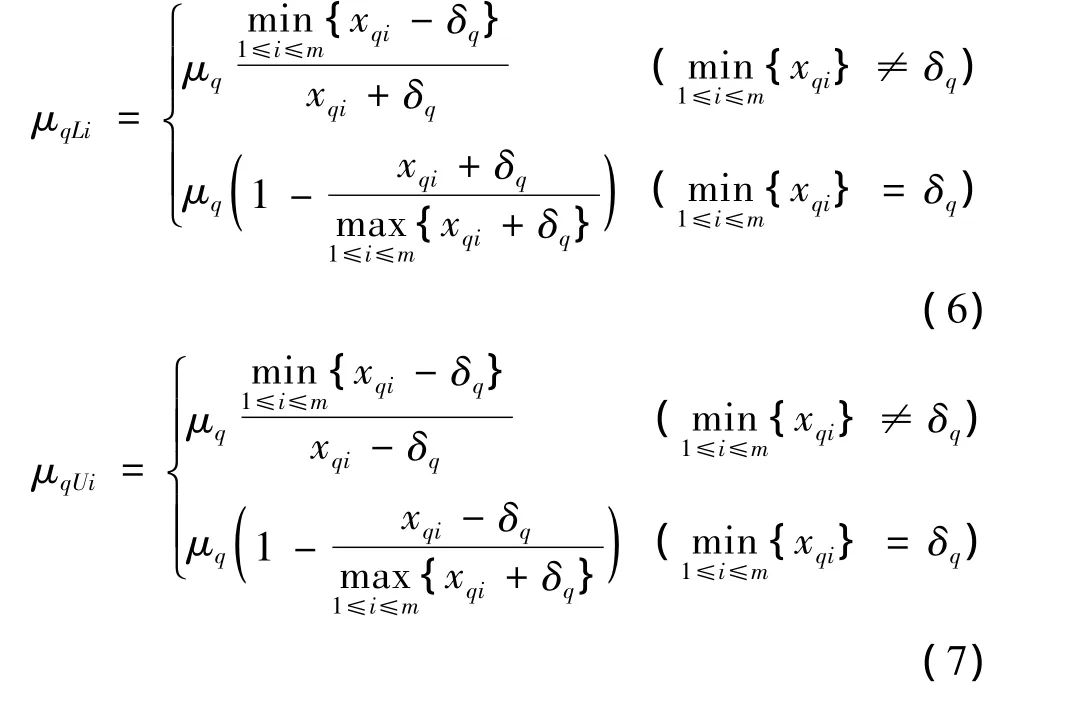
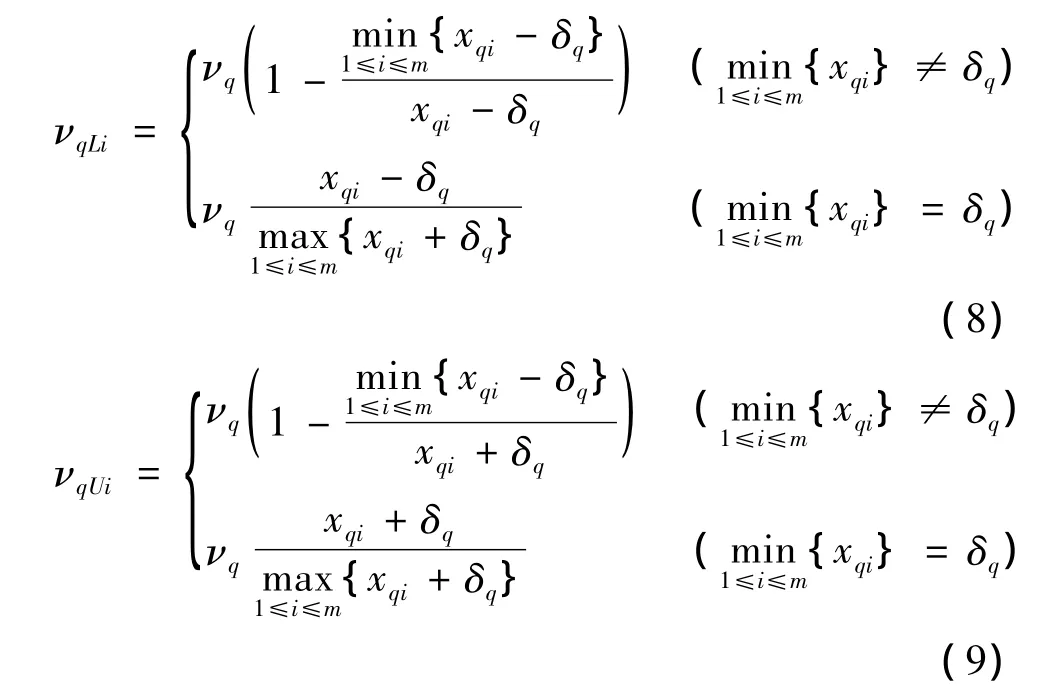
式中:0≤μq+νq≤1。

2.4 距离威胁属性

若敌我双方距离越大，则威胁就越小;反之，威胁就越大。实际距离测量误差大小呈线性关系，其计算公式为:

式中:δSi为距离测量误差;xSi为测得距离;θ4，θ5为参数，且 θ4≥0，θ5≥0。

若测得与第i个目标的距离为xSi，则实际距离范围为［xSi－δSi，xSi+δSi］。距离威胁属性的区间隶属度与区间非隶属度计算公式为:

式中:0≤μS+ νS≤1。以上各式中，μV，νV，μq，νq，μS，νS等参数值是根据对应的因素在威胁评估中的重要程度和空战环境综合确定的。

3 目标属性权重的确定

CE方法是采用重要度采样技术的一种优化方法，能够表征概率分布之间的差异性。因此，将CE原理引入到IVIFS中，同时借鉴逼近理想解排序法的思想，提出采用IVIFCE法确定目标属性权重。

首先，确定目标属性决策矩阵:

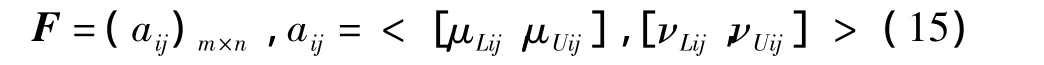
然后，建立求解目标属性权重数学模型:

最后，求解目标属性权重。对式(9)建立Lagrange函数:

分别对ωj和λ求导并使之等于0，解得目标属性权重为:

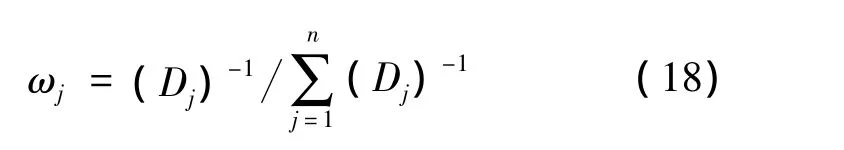
4 信息不确定下空战威胁评估步骤

评估步骤如下:

(1)由式(15)确定目标属性决策矩阵F;

(2)由式(16)～式(18)确定目标属性权重ω;

(3)通过IVIFS加权集结算子计算各目标的综合评价区间直觉模糊值:

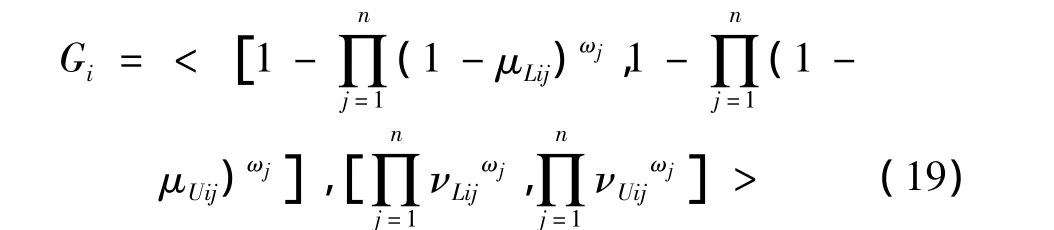
(4)根据IVIFS得分函数计算各目标得分值，即各目标威胁度的大小:

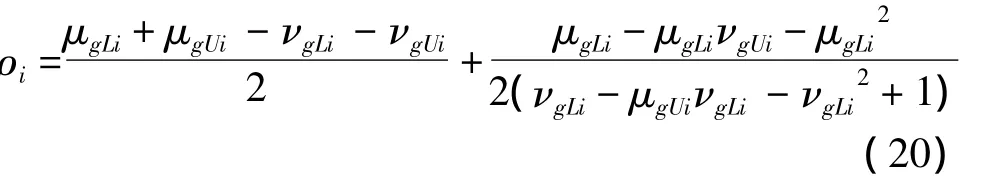
(5)根据 ρi值的大小进行各目标威胁评估排序。

5 仿真结果及分析

某次空战中，我机速度300 m/s情况下遭遇4架敌机，且敌我双方均在作战范围内。我机测量的各敌机目标属性值如表2所示。

根据我机机载设备信息及空战环境复杂性，取速度因素参数 θ1=0.000 1，θ2=0，θ3=0.5，δz=0.5，μV=0.7，νV=0.2;角度因素参数 δq=3，μq=0.8，νq=0.1;距离因素参数 θ4=0.03，θ5=0.2，μS=0.7，νS=0.1。

表2 目标属性信息Table2 Target attribute information

构造目标属性决策矩阵为:

根据式(15)～式(18)计算目标属性权重为:

根据式(19)计算各目标综合评价区间直觉模糊值为:

根据式(20)计算各目标威胁度为:

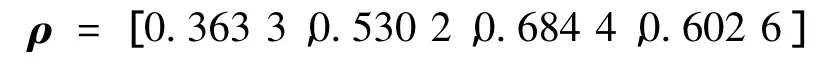
最终各目标威胁排序结果如下:敌机3＞敌机4＞敌机2＞敌机1。

由表2知:敌机3的距离、角度、速度都较其他敌机具有更大的威胁，虽然敌机3的空战能力较弱，但其态势已经构成攻击威胁，而其他敌机态势还需要进一步调整;敌机1和敌机4的角度、距离相同，但敌机4的空战能力和速度都较敌机1具有威胁;敌机1和敌机2的空战能力相同，但敌机2的速度、角度和距离都较敌机1具有威胁，所以敌机1的威胁度最小;由于双方均在作战范围内，敌机4较敌机2的空战能力和速度具有威胁，虽然敌机2的角度较敌机4具有威胁，但敌机4可以通过空战能力和速度进行快速调整，从而弥补角度的劣势。所以，敌机4较敌机2具有威胁。由此可知，分析结果与仿真结果一致。

6 结束语

本文提出了一种信息不确定下空战威胁评估方法。通过IVIFCE方法确定目标属性权重，同时将IVIFS理论成功运用到多目标空战威胁评估中，建立了空战多目标威胁评估数学模型，解决了传统方法在处理测量误差及空战环境造成信息不确定性的问题。仿真结果及分析也表明了该方法的客观性。

［1］ 罗德林，吴文海，沈春林.空战多目标攻击决策综述［J］.电光与控制，2005，12(4):4-8.

［2］ 田涛，王月星，周德云.基于多目标攻击目标选择与战术决策研究［J］.弹箭与制导学报，2006，26(4):374-376.

［3］ 张堃，周德云.基于熵的TOPSIS法空战多目标威胁评估［J］.系统工程与电子技术，2007，29(9):1493-1495.

［4］ Atanassov K T，Gargov G.Interval valued intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1989，35(3):343-349.

［5］ Ye J.Fuzzy cross entropy of interval-valued intuitionistic fuzzy sets and its optimal decision-making method based on the weights of alternatives［J］.Expert Systems with Applications，2011，38(5):6179-6183.

［6］ Chen X W，Kar S，Dan A R.Cross-entropy measure of uncertain variables［J］.Information Sciences，2012(201):53-60.

［7］ Atanassov K T.Operators over interval valued intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1994，64(2):159-174.

［8］ 谢海斌，王中兴，谢国榕，等.基于新精确函数的区间直觉模糊多属性决策方法［J］.数学的实践与认识，2012，42(22):182-188.