自由漂浮空间机器人逆运动学闭环控制

张传海，袁建平

(西北工业大学航天飞行动力学技术国家重点实验室，陕西西安710072)

0 引言

随着空间技术的发展和空间任务的需求，各航天大国都加大力度支持空间机器人技术研究［1］。空间机器人主要由空间机器人本体及搭载在本体上的机械臂组成。当本体的位置和姿态均不受控时，其处于自由漂浮状态，称为自由漂浮空间机器人。采用这种工作状态不但可以节约大量宝贵的能源，延长空间机器人的服役期限，而且可以避免当机械臂接近目标航天器时，位置姿态控制系统工作时突然点火造成的机械臂末端执行器与目标航天器的撞击。因而，自由漂浮空间机器人在空间任务中具有更多的优势。由于自由漂浮空间机器人满足动量守恒，所以机械臂与本体的运动存在动力学耦合，如何协调本体和机械臂的运动使机器人系统完成预定任务就成了首要问题，国内外学者在这方面开展了大量研究［2-8］。

本文通过选取合适的位置和姿态误差信息，给出适用于自由漂浮空间机器人的闭环形式运动控制方法，最后利用系统冗余特性实现了本体姿态零扰动控制。

1 运动学模型

图1给出了自由漂浮空间机器人的示意图。图中，B0为机器人本体;B1～Bn为机械臂连杆;Ji(i=1，2，…，n)为连接部件。

假设:系统各组成部分均为刚体，刚体间的连接均为单自由度转动铰;整个系统不受任何外力及外力矩作用;系统初始的线动量及角动量均为零。基于上述假设，易知系统的质心位置在惯性空间中保持不变，可以作为惯性系OIxIyIzI的原点OI，各连体坐标系Oixiyizi的原点取在各刚体的质心Ci处，坐标轴与刚体的惯性主轴方向一致。

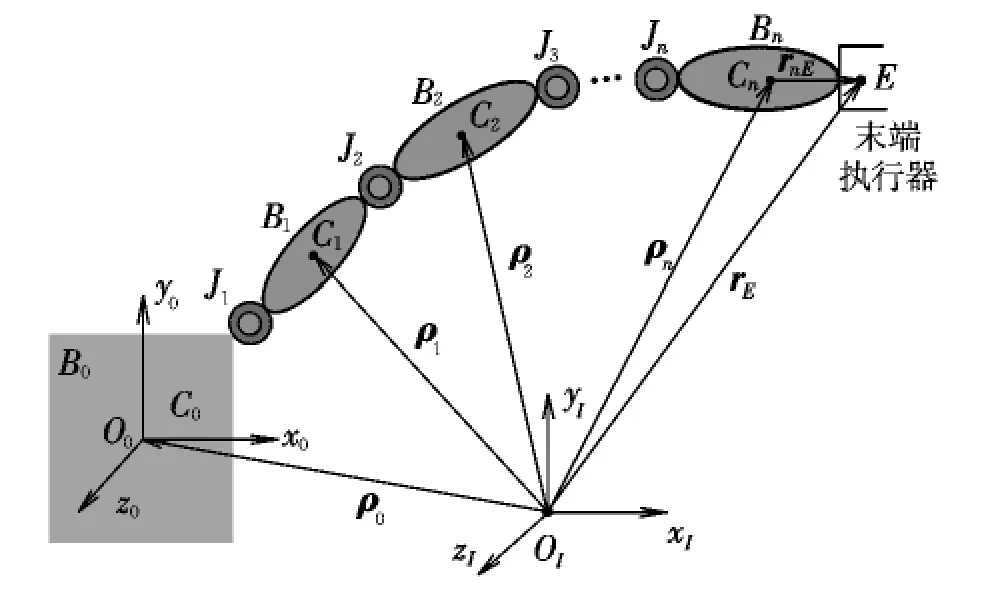
图1 自由漂浮空间机器人示意图Fig.1 Free－floating space robot

本文采用 Roberson－Wittenburg 方法［9］推导自由漂浮空间机器人的运动学模型。Roberson－Wittenburg方法引入图论对刚体的连接关系进行了描述，与以往的推导方法［6-8，10］相比，具有形式整洁、易于程式化和适用广泛的优点。

引入增广体矢量 bji(j=0，…，n;i=0，…，n)，当j=i时，它是由增广体质心指向该刚体质心的矢量;当j≠i时，它是由增广体质心指向该刚体上铰接点的矢量，直接或间接地指向刚体i。进而，刚体Bi(i=0，…，n)在惯性系下的质心位置ρi可以用如下紧凑的形式表示:

刚体Bi质心的速度:

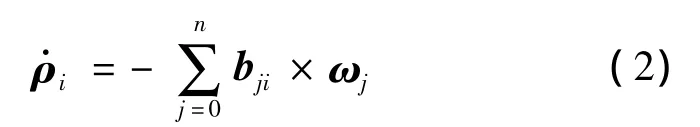
末端执行器的位置矢量rE可以表示为:

对式(3)两边求导，并结合式(2)可得:

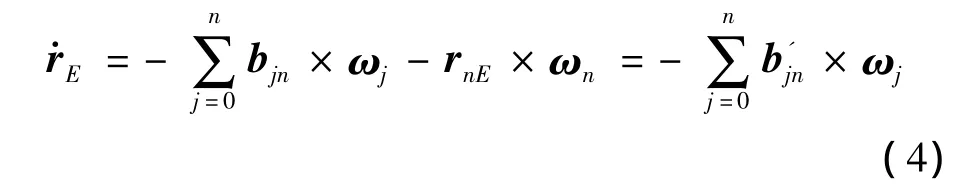
其中:

角速度关系:

式中:Hi为转轴方向矢量矩阵，且:

因为ωE=ωn，则根据式(7)可得空间机器人末端执行器的角速度为:

进而将式(6)带入式(4)，可得末端执行器的线速度为:

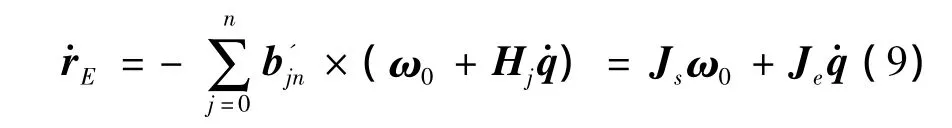
记3×3单位阵为E，则可以将式(8)与式(9)写成更为紧凑的形式:

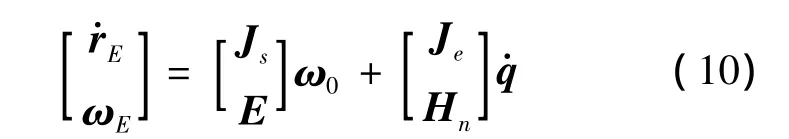
式(10)给出了末端执行器的运动与本体及关节运动的关系。

考虑假设，分别根据线动量和角动量守恒有:

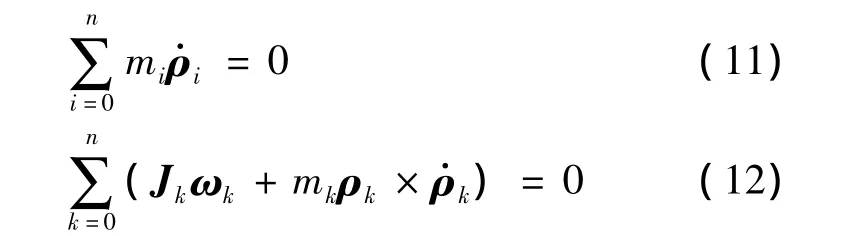
根据式(2)，上式中的第二项可以表示为:

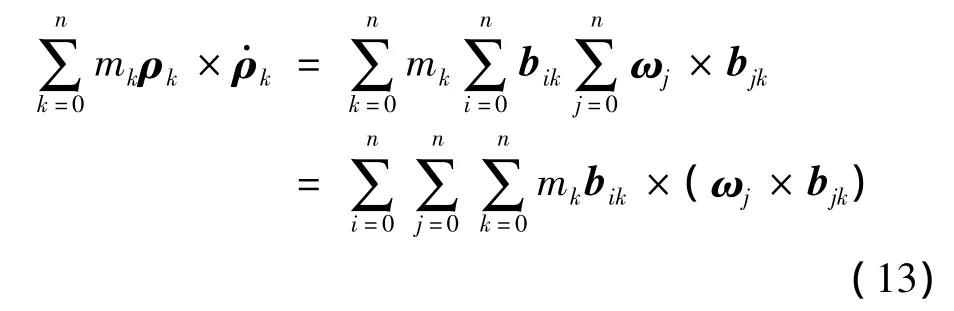
式(13)中双叉乘可以写为张量与矢量乘积的形式:

则式(12)可以表示为:

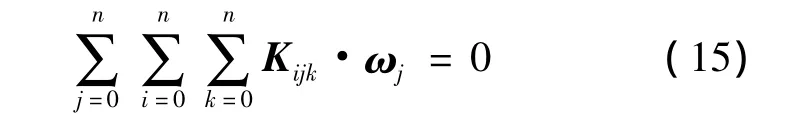
将式(6)带入式(15)，可得:

式(17)给出了本体的运动与关节运动的关系，将其带入式(10)，便可得到末端执行器的运动与关节运动的关系:

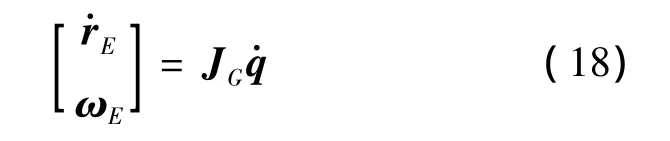
2 闭环形式的逆运动学控制

物体的位移可以用位置矢量r描述，而姿态的描述方法却不唯一。修正罗德里格斯参数(Modified Rodrigues Parameters，MRP)因其与其他姿态描述方式相比具有无冗余、无奇异的优点，广泛应用于姿态估计、姿态控制领域［11-12］。

根据欧拉有限转动定理，MRP定义为:

MRP表示的方向余弦矩阵为:

分别用rd(t)和re(q)表示末端执行器的期望位置和实际位置，定义末端执行器的位置误差为:

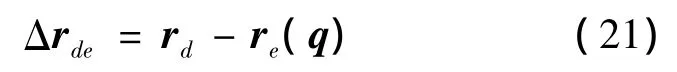
分别用σd(t)，σe(q)表示末端执行器期望姿态和实际姿态，其对应的旋转矩阵分别为Rd和Re，则相对姿态旋转矩阵为:

可以求得与Rde对应的σde为:选取σde作为姿态误差，构造闭环形式的逆运动学方程:

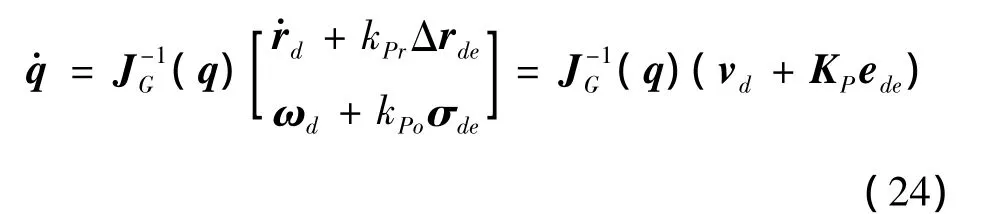
定理1:对于系统式(18)，控制规律式(24)能够保证闭环系统的输出渐近跟踪参考输入。

证明:将式(24)带入式(18)，则系统的控制误差为:

式中:Δωde=ωd－ωe。易知位置误差Δrde是指数收敛的。

构造如下的正定Lyapunov函数:

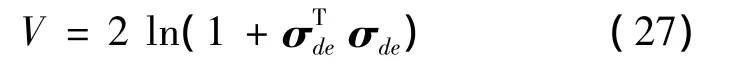
两边对时间求导，结合式(26)和式(23)，可得:

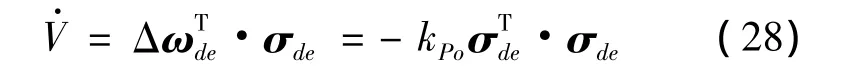
可见姿态误差σde也是收敛的，故系统式(18)在控制规律式(24)下，能够渐近跟踪参考输入。

3 本体姿态零扰动控制

设ms和me分别代表空间机器人本体和末端执行器的任务空间维数，根据文献［7］对于空间机器人冗余性的分析，当关节数n≥ms+me时，机械臂的运动可以协调末端执行器和本体的运动。引入任务优先级的方法［13］，基于以上闭环控制形式的讨论，对于同时存在末端执行器任务和本体任务约束的情形，关节角速率的计算如下:

自由漂浮空间机器人有时为完成复杂的空间作业，保证本体姿态的零扰动是非常必要的，即要求在机械臂的运动过程中，不对本体的姿态产生影响根据上述讨论，此时的关节角速率可按下式求解:

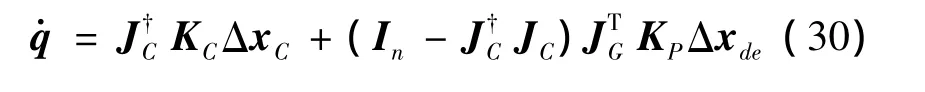
4 仿真结果及分析

为了验证上述闭环逆运动学算法的控制效果，针对1个具有7关节机械臂的自由漂浮机器人设计数值仿真，设机械臂编号分别为i0～i7，质量分别为500.00，20.00，20.00，40.00，40.00，20.00，20.00，40.00 kg;长度分别为 6.00，0.35，0.35，4.00，4.00，0.35，0.35，1.20 m。机械臂构型参考加拿大2号机械臂［14］。 机 械 臂 的 转 动 惯 量 及 D－H(Denavit－Hartenberg)参数如表1所示。

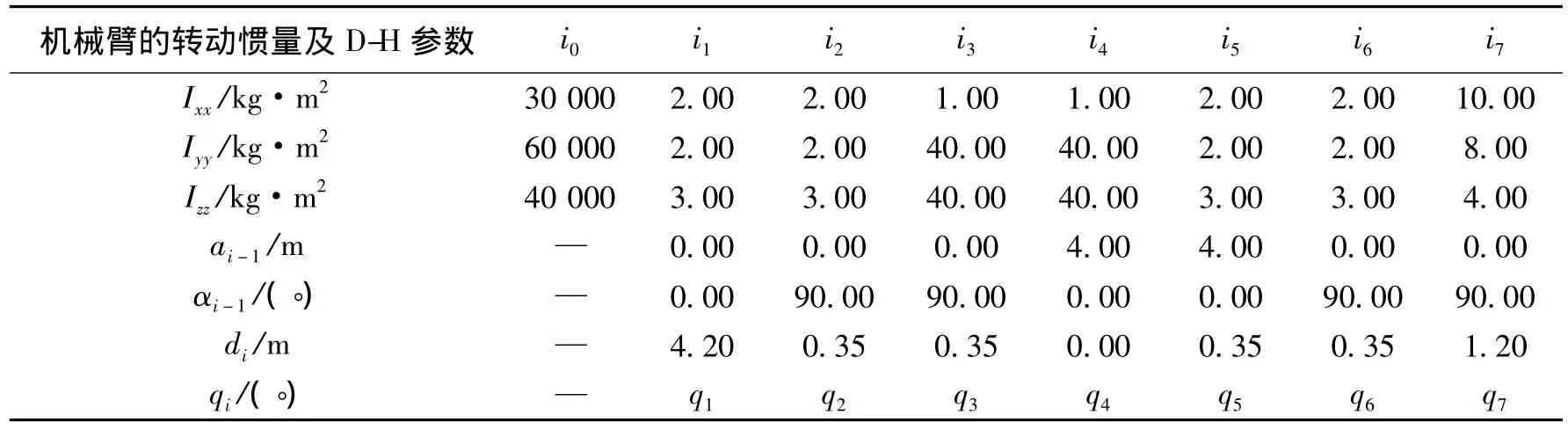
表1 机械臂的转动惯量及D－H参数Table 1 Moment of inertia and the D-H parameters of the robot arm

4.1 初始及目标状态

假设初始本体的体坐标系与惯性系平行，即σoi=0，末端执行器的初始状态:

任务期望的目标状态为:

4.2 期望轨迹

考虑到满足初始和末端时刻速度与加速度均为0，采用五次多项式插值生成期望轨迹。任务时间设计为2 s。

4.3 仿真结果

利用Matlab(R2008a)进行数值仿真，积分采用定步长四阶龙格-库塔算法，积分步长h=0.002 s。

算例1仅存在末端执行器任务约束，即控制末端执行器由初始状态按期望轨迹到达目标状态，而不考虑其对本体姿态的影响，按式(24)计算，增益矩阵KPr=10E，KPo=20E。为了考察初始误差对控制的影响，设末端执行器初始位姿分别存在10－2，10－3量级的随机误差，仿真结果如图2～图5所示。

图2给出了各关节角速率随时间变化的规律，可以看出控制输入光滑平缓。图3和图4分别给出了末端执行器的位置和姿态误差，可以看出，在存在初始误差的情况下，误差随时间是收敛的，且在0.6 s误差已经减小到10－4量级。关节运动对本体的姿态干扰如图5所示，可以看出关节运动对本体姿态产生了扰动。

算例2同时存在末端执行器和本体任务约束，即实现末端执行器任务的同时保证了本体姿态零扰动。为了满足冗余性的要求，末端执行器的任务仅考虑姿态约束，按式(30)计算，假设初始无误差，增益矩阵 KP=100E，KC=40E，结果如图 6～图 8所示。

从图6可以看出，控制输入仍然能够保证光滑平缓。图7给出了末端执行器的姿态控制误差，由于本体姿态任务的存在，其误差为10－3量级，相比于算例1有所增大。从图8的关节运动对本体的姿态干扰情况可以看出，干扰在10－6量级以下，可以看作姿态零扰动。

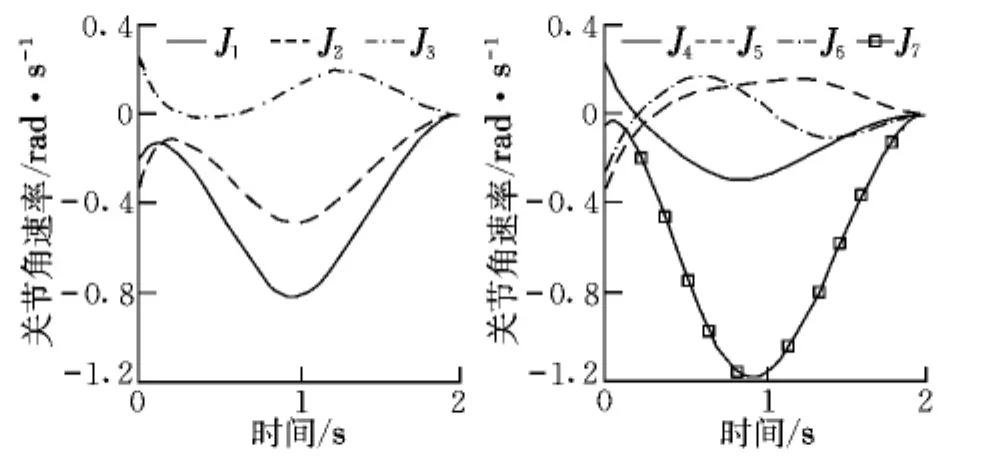
图2 关节角速率Fig.2 Joint velocity

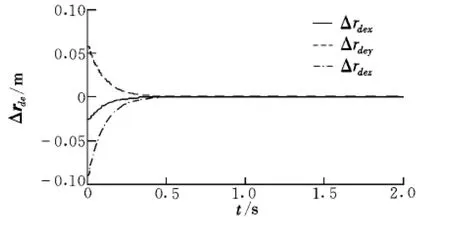
图3 末端执行器的位置误差Fig.3 Position errors of the end－effector

图4 末端执行器的姿态误差Fig.4 Attitude errors of the end－effector

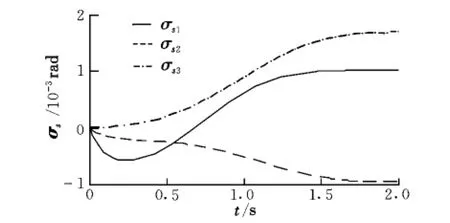
图5 本体姿态Fig.5 Base attitude

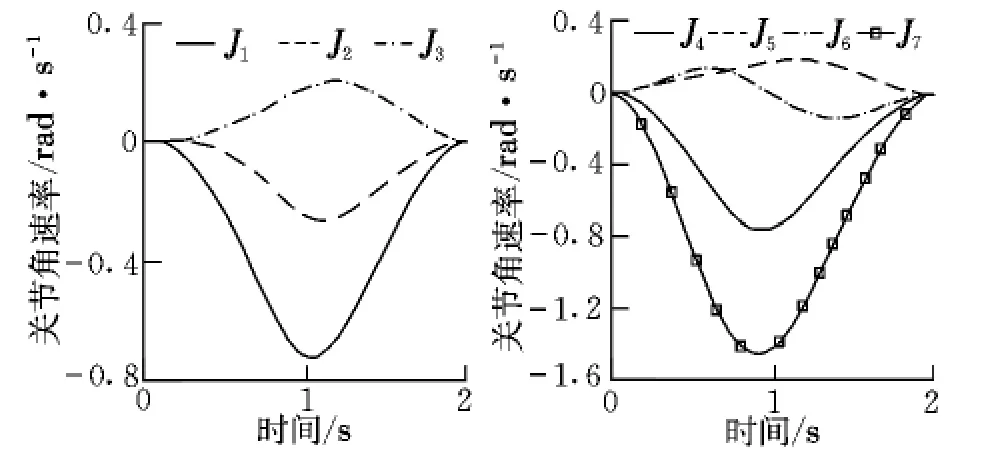
图6 关节角速率Fig.6 Joint velocity

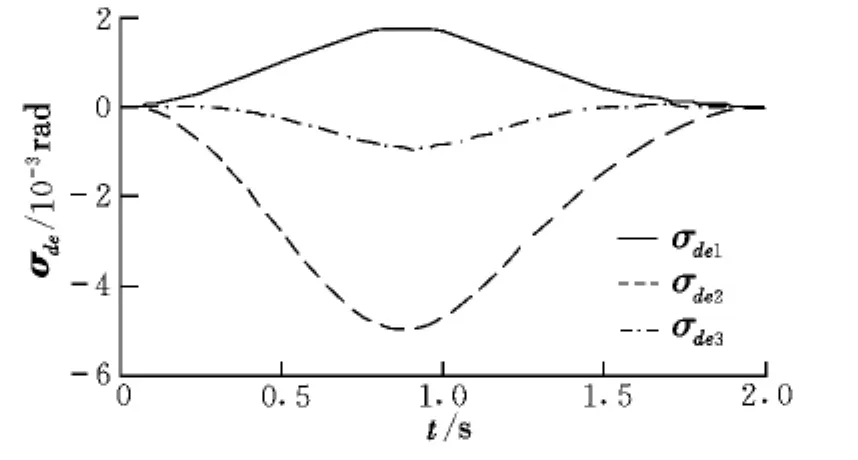
图7 末端执行器的姿态误差Fig.7 Attitude errors of the end－effector

图8 本体姿态Fig.8 Base attitude

5 结束语

本文针对自由漂浮空间机器人的控制特点，通过引入适当的反馈信息，给出了一种闭环形式的逆运动学控制算法。在此基础上，讨论了利用系统的冗余特性实现本体姿态零扰动的方法。通过仿真表明，该方法可以有效解决自由漂浮机器人运动控制问题，并且可以用于本体和末端执行器任务约束同时存在的情形，具有易于实现、稳定性好的优点。

［1］ 张文辉，叶晓平，季晓明，等.国内外空间机器人技术发展综述［J］.飞行力学，2013，31(3):198－202.

［2］ Vafa Z，Dubowsky S.On the dynamics of space manipulators using the virtual manipulator approach，with application to path planning［J］.Journal of Astronautica Sciences 1990，38(4):441－472.

［3］ 梁斌，刘良栋，李庚田，等.空间机器人的动力学等价臂［J］.自动化学报，1998，24(6):761－767.

［4］ Nenchev D，Yoshida K，Umetani Y.Analysis，design and control of free－flying space robots using fixed－attitude－restricted Jacobian Matrix［C］∥Proceeding of the Fifth International Symposiumon Robotics Research.MIT Press Cambridge，1990:251－258.

［5］ Liu X D，Baoyin H X，Ma X R.Optimal path planning of redundant free－floating revolute－jointed space manipulators with seven links［J］.Multibody Systems Dynamic，2013，29(1):41－56.

［6］ Umetani Y，Yoshida K.Resolved motion rate control of space manipulators with generalized Jacobian matrix［J］.IEEE Transactions on Robotics and Automation，1989，5(3):303－314.

［7］ Nenchev D，Umetani Y，Yoshida K.Analysis of a redundant free－flying spacecraft/manipulator system［J］.IEEE Transactions on Robotics and Automation，1992，8(1):1－6.

［8］ Siciliano B.A closed－loop inverse kinematic scheme for online joint－based robot control［J］.Robotica，1990，8(3):231－243.

［9］ Wittenburg J.Dynamics of systems of rigid bodies［M］.Teubner，Stuttgart，1977:1－224.

［10］Kreutz－Delgado K，Long M，Seraji H.Kinematic analysis of 7 DOF manipulators［J］.The International Journal of Robotics Research，1992，11(5):469－481.

［11］ Akella M R.Rigid body attitude tracking without angular velocity feedback［J］.Systems and Control Letters，2001，42(4):321－326.

［12］ Gohary A E，Tawfik T E S.Attitude stabilization using modified Rodriguez parameters without angular velocity measurements［J］.World Journal of Mechanics，2011，1(2):57－63.

［13］ Nakamura Y，Hanafusa H，Yoshikawa T.Task－priority based redundancy control of robot manipulators［J］.International Journal of Robotics Research，1987，6(2):3－15.

［14］ Gibbs G，Sachdev S.Canada and the international space station program:overview and status［J］.Acta Astronaut，2002，51(1－9):591－600.