酸雨环境下受腐蚀混凝土弹性模量灰色预测

徐 为，刘嫦娟

（1.诸城市财政局，山东 诸城262200；2.秦皇岛华成建筑设计咨询有限公司，河北 秦皇岛066000）

0 引言

我国是继欧洲、北美之后的世界第三大酸沉降区[1]。研究表明[2]，近几年我国的酸雨污染还在扩大和加重。混凝土作为用量最大的建筑材料之一，其耐久性问题是研究整个钢筋混凝土结构耐久性的基础，具有重要意义。而混凝土弹性模量既是混凝土结构设计的重要参数，又是表征其内部破坏的重要参数，因此探讨受酸雨腐蚀混凝土弹性模量的劣化规律非常必要。

从1872 年英国化学家Smith 首次提出酸雨的概念[3]，一直到现在酸雨引起了各国学者的普遍关注，并开展了对酸雨各方面的研究。仅仅针对酸雨对混凝土力学性能的劣化，国内外科研工作者就展开了大量的试验研究[4-8]和定性的机理分析[9]。迄今为止，关于受酸雨腐蚀后混凝土弹性模量变化规律的试验研究和理论分析较少。胡晓波等（2008）以喷淋光照循环方式模拟酸雨对C50 混凝土的侵蚀，得到了受侵蚀混凝土抗压强度、弹性模量等力学性能指标，但试件个数偏少，缺少进一步的理论分析。张英姿等（2010，2012）以试验室加速腐蚀方法模拟酸雨（pH 值分别为1.5、2.5 和3.5）对C40 混凝土的腐蚀，得到了腐蚀后混凝土的重量、抗压强度、弹性模量及抗拉强度等力学变化规律，并应用复合材料细观损伤力学建立了混凝土弹性模量的理论计算模型[10]。综上所述，以上学者的试验研究大部分是局限于劣化混凝土定性的机理分析及其质量、抗压强度等指标的变化，涉及弹性模量的试验数据较少，不足以反映侵蚀后混凝土弹性模量的变化规律，对受酸雨腐蚀混凝土的弹性模量缺乏系统的试验研究和深入的理论探讨。由于混凝土材料本身是离散性较大的材料，在使用过程中环境因素、人为因素等各因素间相互作用、相互制约，且各因素间又具有高度的不确定性，故问题具有较大的复杂性。灰色系统理论在数据处理方面，尤其在“小样本”、“贫信息”且无较好分布规律条件下，生成、开发并提取有价值信息，比基于回归分析的传统方法有明显优势，甚至比需要大量训练样本的神经网络方法更为方便。近年来灰色理论也在土木工程中得到了大量应用[11-13]，张英姿[12]和李北星[13]分别建立了不同腐蚀介质下的混凝土抗压强度灰色理论模型，目前用灰色系统理论对酸雨条件下的弹性模量研究还较少，故本文就是将灰色系统理论引入混凝土弹性模量的研究中，尝试建立GM 模型预测受酸雨腐蚀混凝土的弹性模量，为受酸雨侵蚀混凝土的力学性能劣化规律预测提供一个简便可行的途径。

1 灰色GM模型

GM（1，1）模型是灰色系统的基本模型，一般是针对离散数列而言的，它建模所需的信息较少，对处理无规律或者任何分布规律的条件下，建模的精度较高，能较好地反映出系统的实际状况，符合受酸雨腐蚀混凝土弹性模量的测试数据少、不确定性因素多的特点。

设序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，将x(0)(n)取为时间轴的原点，则称t＜n为过去，t=n为现在，t＞n为未来。GM（1，1）模型时间响应式为：

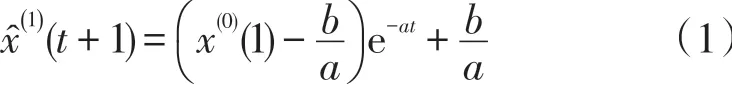
其累减还原值为：

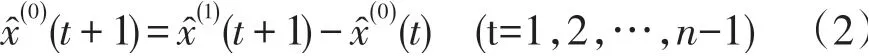
当t≤n时，称为模型模拟值；t＞n时，称为模型预测值。建模的主要目的是预测，为提高预测精度，要保证有充分高的模拟精度，尤其是t=n时的模拟精度。设原始数据序列则：

（1）用X(0)=(x(0)(1),x(0)(2),…,x(0)(n))建立的GM（1，1）模型称为全数据模型GM（1，1）；

（2）若t0＞1，用X(0)=(x(0)(t0),x(0)(t0+1),…,x(0)(n))建立的GM（1，1）模型称为部分数据模型GM（1，1）；

（3）设x(0)(n+1)为最新信息，将x(0)(n+1)置入X(0)，用X(0)=(x(0)(1),x(0)(2),…,x(0)(n),x(0)(n+1))建立的模型称为新信息GM（1，1）模型；

（4）置入最新信息x(0)(n+1)，去掉最老信息x(0)(1)，用X(0)=(x(0)(2),…,x(0)(n),x(0)(n+1))建立的模型称为新陈代谢GM（1，1）模型。

在实际建模中，原始数据序列的数据不一定全部用来建模。在原始数据序列中取出一部分数据，就可建立一个模型。根据文献[13]的研究成果，从预测的角度而言，新陈代谢模型是最理想的模型。针对酸雨中混凝土的力学性能变化特点，故本文采用新陈代谢模型预测受酸雨腐蚀混凝土的弹性模量灰色模型。

2 模型的建立

本文用于分析的试验数据取自受不同pH 值模拟酸雨溶液腐蚀的混凝土抗压性能试验得到的研究结果[4]。试验中混凝土标号为C40，试件尺寸为150mm×150mm×300mm，酸雨溶液的pH 值分别为1.5、2.5和3.5。在3种浓度的腐蚀溶液中，混凝土试件的腐蚀时间有所不同，每组试件有3 个试块；混凝土抗压性能通过YAW—YAW2000A 型200t 微机控制电液饲服压力试验机测得。3种腐蚀液中棱柱体试块的加载方式相同，均采用现行规范规定的混凝土抗压强度试验进行加载。

2.1 pH值为1.5的模拟酸雨溶液

在GM模型建立中，假设全数据序列为：

去掉最老信息，输入一个最新信息，则新陈代谢建模序列为：

由式（1）可得到当pH=1.5 时，a=0.022，b=45.154。其时间响应式为：

由式（2）及式（3）得到的预测值及相对误差列于表1，其平均相对误差为0.907%。

表1 模型计算结果与试验结果比较表（pH=1.5）

2.2 pH值为2.5的模拟酸雨溶液

在GM模型建立中，假设全数据序列为：

去掉最老信息37.242，输入一个最新信息37.465，则新陈代谢建模序列为：

同理，由式（1） 可得到当pH=2.5 时，a=0.001，b=42.467。其时间响应式为：

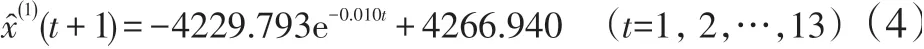
由式（2）及式（4）得到的预测值及相对误差列于表2，其平均相对误差为2.310%。

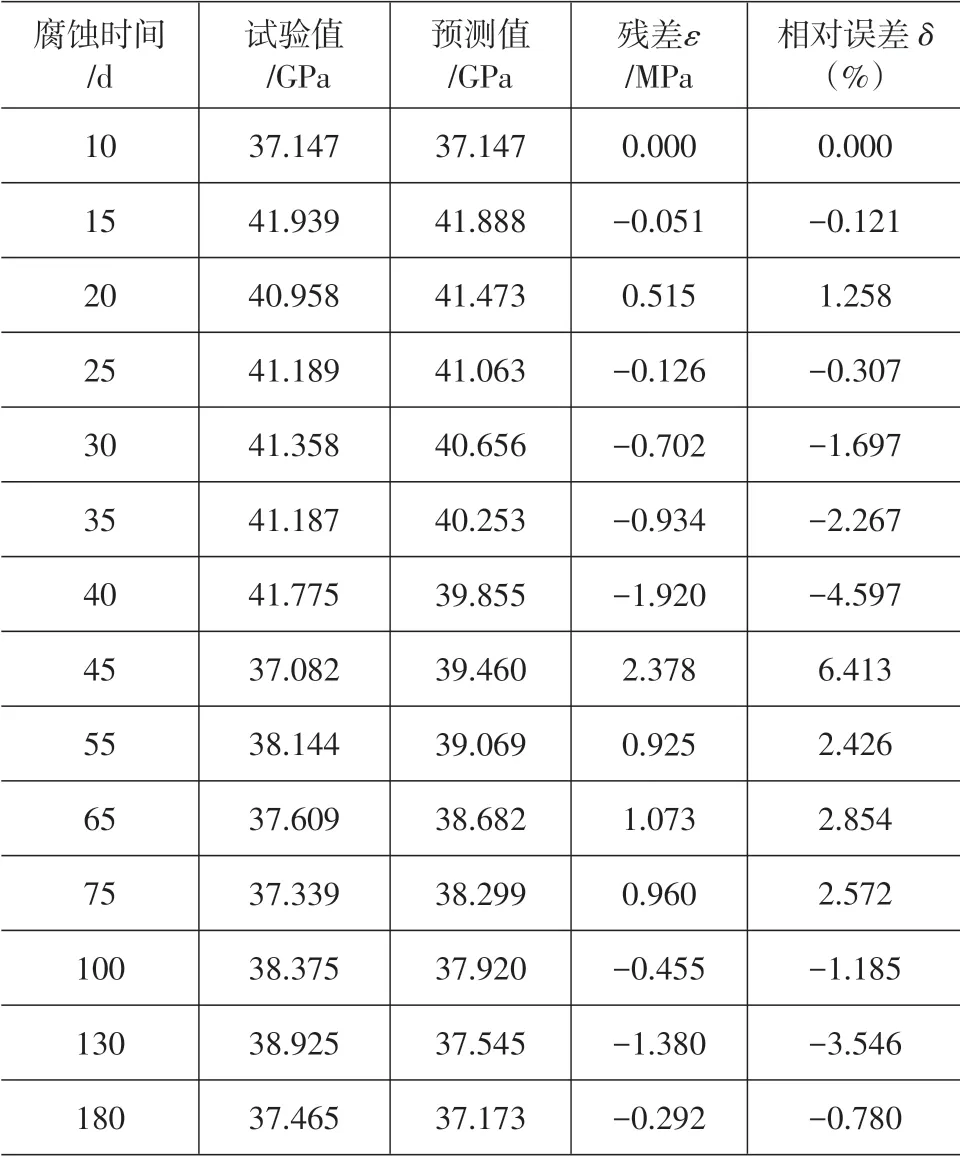
表2 模型计算结果与试验结果比较表（pH=2.5）

2.3 pH值为3.5的模拟酸雨溶液

在GM模型建立中，假设全数据序列为：

去掉最老信息39.177，输入一个最新信息37.078，则新陈代谢建模序列为：

同理，由式（1） 可得到当pH=3.5 时，a=0.0004，b=38.8566。其时间响应式为：

由式（2）及式（5）得到的预测值及相对误差列于表3，其平均相对误差为2.123%。

表3 模型计算结果与试验结果比较表（pH=3.5）

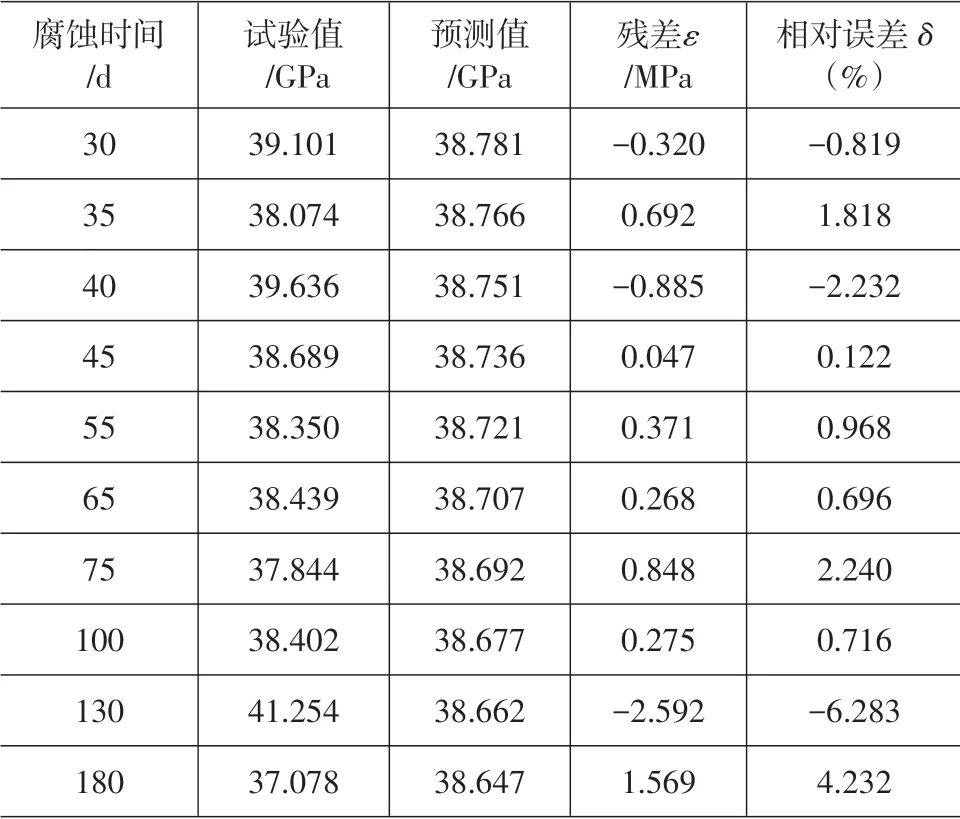
表3（续）

2.4 模型检验及分析

由表1～表3 可以看出，虽然不同pH 值模拟酸雨溶液试验值存在较大波动，但模型预测结果与试验结果的相对误差都在7%以内，且平均相对误差都较小，未超过3%，这表明新陈代谢GM（1，1）模型对有波动的序列也具有较好的预测精度。

3 结论

针对受侵蚀混凝土弹性模量的变化特点，基于对pH值分别为1.5、2.5和3.5的模拟酸雨溶液腐蚀混凝土的静力抗压弹性模量试验研究结果，本文建立的新陈代谢GM（1，1）模型能有效地预测受酸雨腐蚀混凝土的弹性模量。

[1] 李铁锋.环境地质学概论[M].北京：中国环境科学出版社，1996：56-57.

[2] 张新民，柴发合，王淑兰，等.中国酸雨研究现状[J].环境科学研究，2010，23（5）：527-531.

[3] W H Smith. Air pollution and forests: Interactions between air contaminants and forest ecosystems[M]. NewYork: Springer-Verlag,1981.

[4] 张英姿，范颖芳，刘江林.模拟酸雨环境下C40混凝土抗压性能试验研究[J].建筑材料学报，2010，13（1）：105-110.

[5] 张英姿，范颖芳，李宏男，等.模拟酸雨环境下混凝土抗拉性能试验研究[J]. 建筑材料学报，2012，15（6）：857-862.

[6] HIROSHI Okochi, HIDEKI Kameda, Shin-ichi Hasegawa,et al. Deterioration of concrete structures by acid deposi⁃tion-an assessment of the role of rainwater on deterioration by laboratory and field exposure experiments using mortar specimens[J]. Atmospheric Environment, 2000(34): 2937-2945.

[7] KONG L H, JAMES G. Concrete deterioration due to acid precipitation[J]. ACI Materials Journal, 1987, 84(2): 110-116.

[8] FATTUHI N I, HUGHES B P. The performance of cement paste and concrete subjected to sulphuric acid attack[J].Cement and Concrete Research,1988,18(4):545-553.

[9] Xie S,Qi L,Zhou D.Investigation of the effects of acid rain on the deterioration of cement concrete using accelerated tests established in laboratory[J]. Atmospheric Environ⁃ment,2004(38):4457-4466.

[10] 张英姿，赵颖华，范颖芳.受酸雨侵蚀混凝土弹性模量研究[J].工程力学，2011，28（2）：175-180.

[11] Der-Hsien Shen,Chia-Ming Wu,Jia-Chong Du.Applica⁃tion of Grey Model to Predict Acoustical Properties and Tire/Road Noise on Asphalt Pavement[R]. Toronto: 2006 IEEE Intelligent Transportation Systems Conference,2006.

[12] 张英姿，范颖芳，赵颖华.受盐酸腐蚀混凝土抗压强度的灰色预测模型[J].建筑材料学报，2007，10（4）：397-401.

[13] 李北星，蔡老虎.基于灰色系统的混凝土酸性化预测模型研究及应用[J]. 硅酸盐学报，2013，41（10）：1375-1380.

[14] 刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2004.