基于线段模型的高速公路安全与流量关系研究

刘力玮，马博渊，王章宇，邹睿航

（1.北京工商大学经济学院，北京100048；2.北京工商大学计算机与信息工程学院，北京100048；3.北京工商大学材料与机械工程学院，北京100048）

1 模型理论

1.1 现实生活中的超车情形

现实中左驾右行的驾驶模式会受到多方面因素的影响，例如司机的驾驶习惯，汽车性能，道路性能。理想中，若所有车辆以相同速度行驶，则汽车行驶中不会发生超车，也不会被超车。但实际情况是每辆车的行驶速度并不相同，超车的发生次数也随车流量密度的变化而不断变化。

汽车是有空间和质量的物体，在行驶中会因驾驶不当发生碰撞。超车过程会受到多种因素的影响，如前后车间距，被超车辆对超车车辆的视线遮挡角度，超车车辆左侧并道后在超车车辆后方是否存在也正在超越其他个体的车辆等。若单独从微观角度分析超车过程中的影响因素，诸多因素并不相互独立，难以考虑所有影响因素来建立模型；若从某单一因素对超车过程的影响入手建立模型，又不能完整地体现超车过程中复杂的因素影响。所以在本文的左驾右行模型中，将车视为没有质量，没有空间的点。

超车的过程分为三个阶段，第一阶段，向左并道准备超车；第二阶段，直线行驶，直到与被超车辆之间的距离符合行驶安全距离；第三阶段，向右并道，回归初始状态。可以得出，超车过程是一个在时间与空间上都有变化的过程量。在模型中，车辆行驶都遵守不超车时在右侧行驶的规则，只有在超车的时候才会往左边移动一条车道完成超车。所以，模型将高速公路视为两车道。

真实情况车道上的车辆有轿车、货车、巴士等多种车辆。每种车在计算车流量时的数量不同，例如7 坐及以下轿车为1veh/h，拖挂货车为3veh/h。模型中将所有的车辆都视为7 坐以下的轿车，即所有的个体车辆所占的车流量都为1veh/h。

1.2 模型整体思想

在模型中，不考虑超车过程中的变道时间，忽略变道过程中向左前行驶与右前行驶造成的相较于直线行驶距离的增加。将所有点放在一条线段上运动，每个点的运动速度恒定，总体的速度呈正态分布。当点之间发生一次重叠的时候，记为一次超车。点与点之间的重叠是瞬时的，当某一点与前一点重合之后，这两个点的运动状态不发生任何变化，保持两个点原来的运动状态继续运动，然后计算当点的运行状态处于稳定状态下的重叠的次数。也就是说当高速公路上的车辆成均匀分布，车辆的速度程正态分布。

参考NS 模型与上文中提到的模型，发现左驾右行模型涉及正常行车、超车、自由通行状态、无法自由通行状态（堵车）。影响因素包含车流量、道路中车辆密度和行车速度，这些因素并不独立。在一个模型中将这些并不相互独立的变量同时考虑需要庞大的计算量，而且不能保证准确性。

通过何种建模方式，保证模型准确性，同时使各个因素之间的相关性影响减小到最小，是模型开发的理想结果。在此需要理解车辆遵守左驾右行模型时的超车模型，将车看做质点之后，这些点之间的超越不存在换道，只要有一次重叠就是发生一次超车。

2 普通超车模型实例

在模型建立初期，为了简化模型，排除了一些变量因素。例如司机的驾驶习惯、车流量对汽车行驶速度的影响、汽车速度对车间距的影响、车间距与超车概率的关系。这些影响因素会在之后加入，完善模型，进而得到和现实情况比较接近，且为两车道的一条高速公路的数据，并将这个数据带入模型之中。

根据沈大高速公路的车流流量数据，在2004 年之前，沈大高速公路的最大承载能力为55 000veh/24h，最低承载能力22 000veh/24h。此处的承载能力是双向行驶的承载能力，因此应该除以2，得到单向行驶的最高承载能力与最低承载能力。设计限速为50～120km/h。根据沈大高速公路的最大与最小承载能力，可以得到车辆放行的频率0.01～0.32veh/s。

模型将所有车辆看成单位为1veh 的点，并且所有点在一条线段上运行。查阅资料后，未能找到其他与本模型相同假设的模型。

因此，在本文模型中采用仿真试验的方法模拟一条高速公路中超车发生的次数。通过对照试验的方法研究：

（1）高速公路限速上下限对汽车行驶实际情况造成的影响；

（2）高速公路平均行驶速度对汽车行驶实际情况造成的影响。

在设计“高速公路限速上下限对汽车行驶实际情况造成的影响”时，考虑到高速公路中所有车辆的行驶速度应该服从正态分布，根据期望速度与速度标准差可以凭借方差为界确定汽车速度的上下限。

2.1 同一正态分布下的车流量与超车次数的关系

通过对沈大高速公路车辆数量和行驶速度分析得出，二者之间服从以23.68m/s 为期望，以4.83m/s为标准差的正态分布，及X～N(23.68，4.832)。沈大高速公路不同车速及其数量关系如图1所示。

根据上述的模型介绍，在线段起始端依照一定的流量抛出随机速度的点，最后计量在一定时间内抛出的点在线段上碰撞次数，并以发生的碰撞次数来代替超车次数，最后进一步说明车流量与安全的权衡。

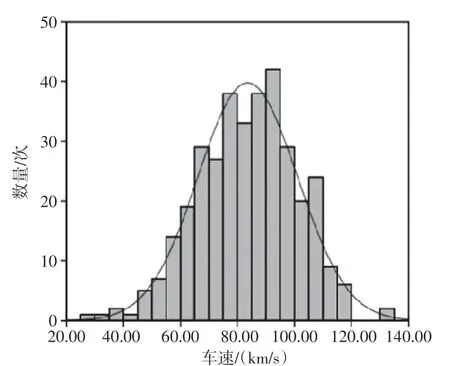
图1 沈大高速公路不同车速及其数量直方图

2.1.1 模型假设

本文模型采用以下假设：（1）把车辆视为质点；（2）沈大高速公路为一条直线，其全长为270km；（3）车辆在行驶过程中只有在超车时才会发生危险，即超车次数越多，发生危险的概率也就越大；（4）车辆放行速度是以在沈大高速公路测得的不同车速及其数量的数据拟合出的正态分布X～N(23.68，4.832)，同时是随机抛出的。

2.1.2 模型方法

在线段的的起始点向线段中抛出一定流量的点（点单位为veh，流量单位为veh/h），待点在270 000m 的线段上均匀布满后，开始计算在一定时间内的质点碰撞次数，且为了排除偶然因素，只计量均匀状态下1h 的碰撞次数；在其他条件（线段长度、点抛出的正态分布、点均匀布满时间及记录时间）不变的情况下，改变抛出的车流量，以0.01作为车流量变动的最小单位；引入C++语言对上述过程进行编程计算，并根据得出的统计量使用MATLAB 拟合、修匀并给出相应表达式。通过引入C++语言对上述过程进行编程计算，得出的数据如表1和图2所示。

表1 车流量与超车次数的关系

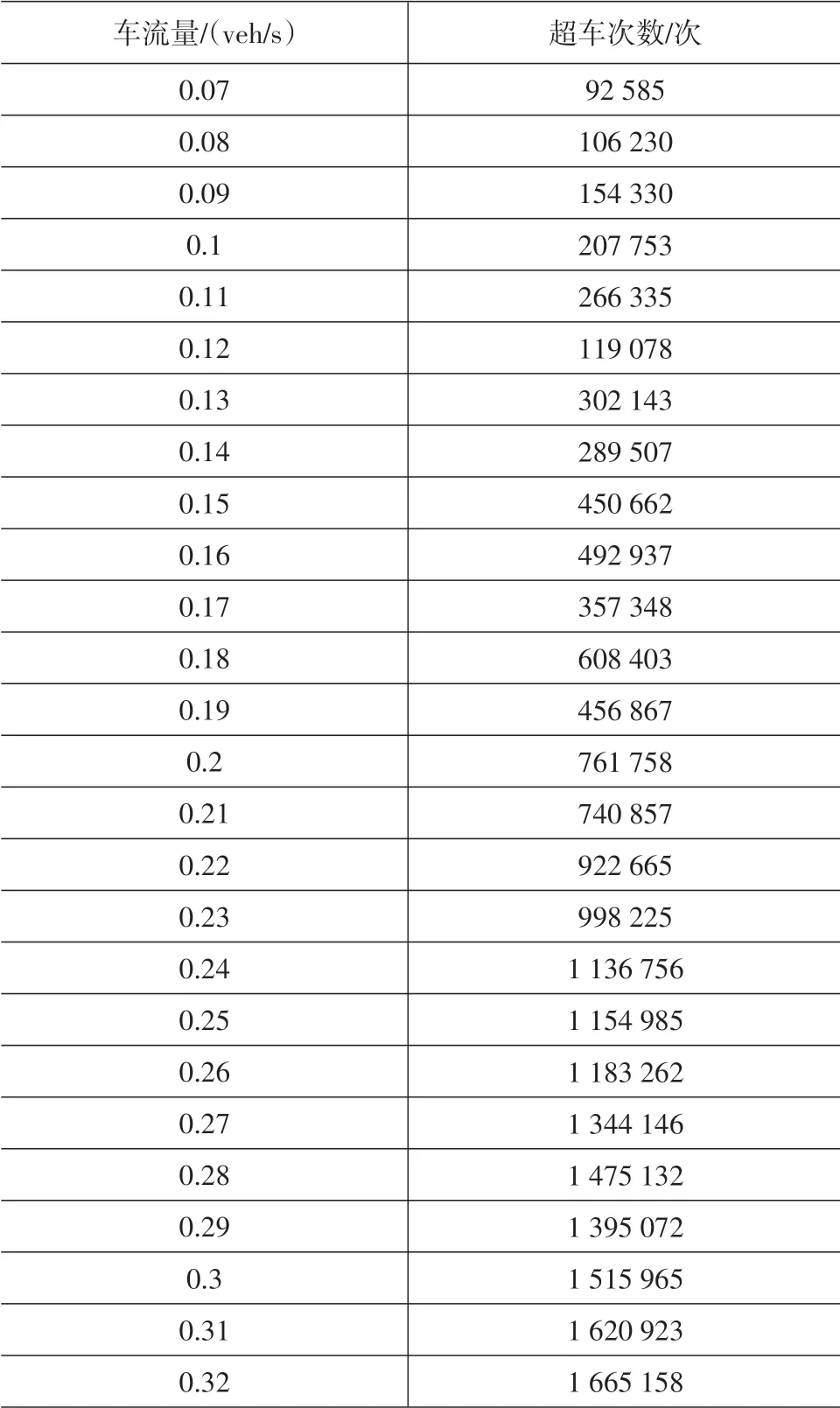
表1（续）

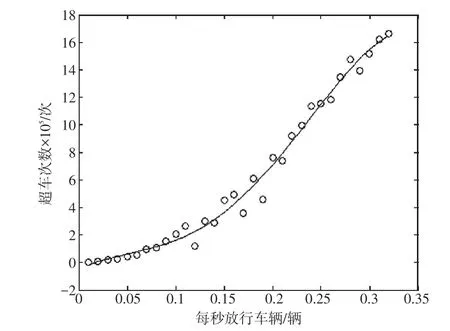
图2 车流量与超车次数的关系

根据得出的统计量使用MATLAB 拟合、修匀，相应表达式为：

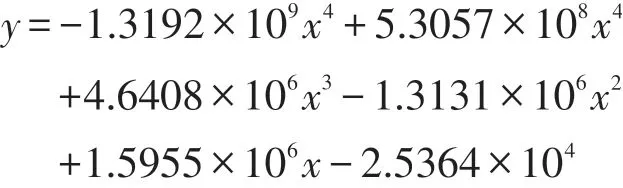
2.1.3 模型分析

在定量分析中，通过1h 的计量，可以清晰地看到随着车流量的增加，超车次数在逐渐变大，但当车流量达到0.40veh/h 以后，超车次数变得稳定，也就是说在车流量达到0.40veh/h 后，曲线一改前一阶段的变化规律，趋于稳定。此点过后，模拟的曲线性质发生了极大变化。

模型函数的二阶导函数图像如图3所示。

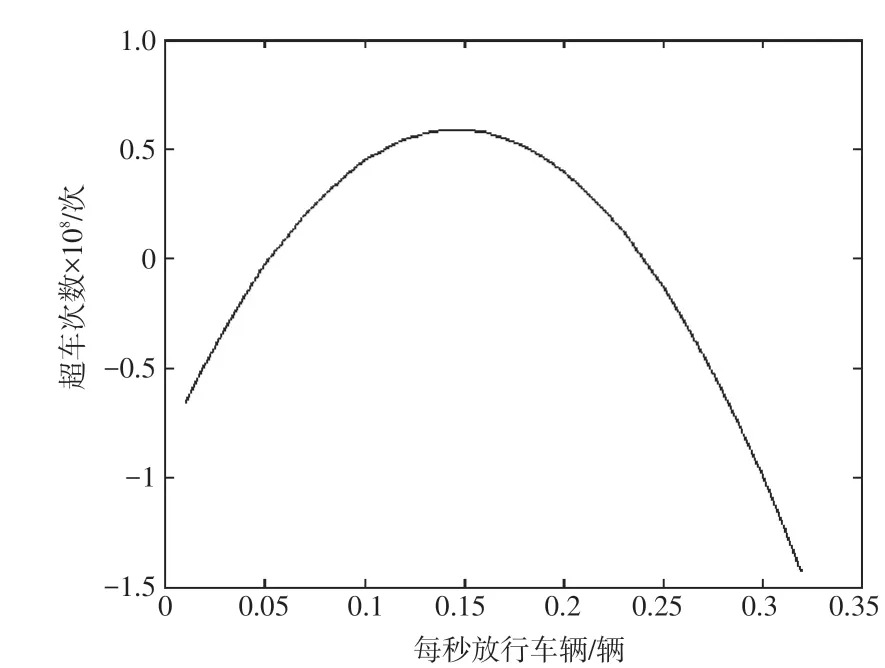
图3 车流量与超车次数函数的二阶导数

在二阶导数中，如果x∈[ ]a,b,且时，在此区域函数为凹函数，如果x∈[b ,c],并且时，在此区域函数为凸函数，此时x=b 时为凹凸函数的临界点，此二阶导数的临界点为：x1=0.02，x2=0.2403。在当车流量临界点，原函数的凹凸性瞬间发生变化，就可以依据这两个点确定最佳的车流量，即0.05veh/s和0.24veh/s（对原数据向下取证），但是车流量为0.02veh/h，道路的车流量极少相对0.24veh/s 时更加浪费资源，最后确定最佳车流量应确定为0.24veh/s。

现考虑车流量对超车率的影响，认为超车率越高潜在风险就越大。根据已有文献，可知车流量达到500veh/h，即0.14veh/s时超车率最大，同时也是潜在风险最大的点的车流量，随着车流量的边缘化，超车率逐渐变小，同时潜在风险也在变小。当车流量为0.24veh/s 时，超车率为约为5%，潜在风险为最高时的5%/0.13%=38.46%，这样认为是相对安全的。实际放行车辆与超车率的关系如图4所示。

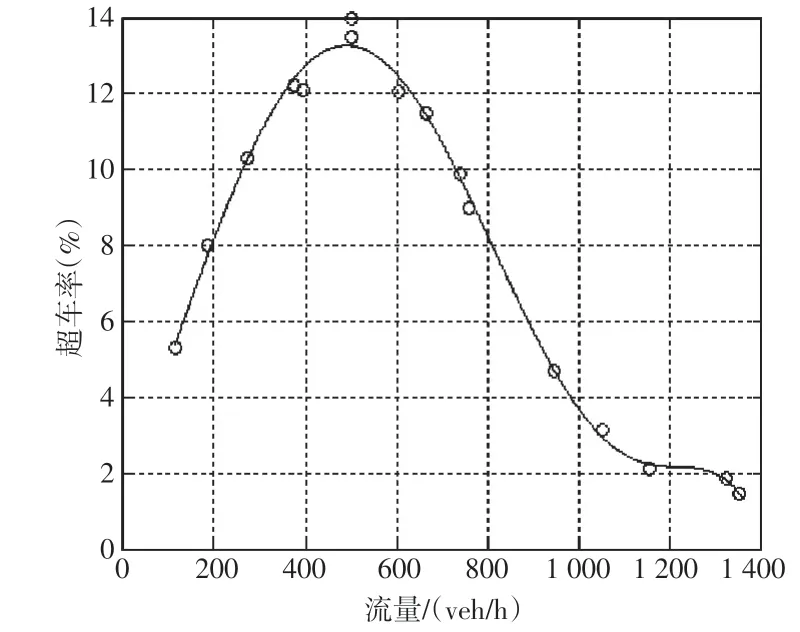
图4 实际放行车辆与超车率的关系

2.1.4 模型结论

在安全和流量同时权衡时，可以车流量为0.24veh/s为基础进行调整，调整量为0.01veh/s，即控制流量在0.23～0.25veh/s 时交通更有效率且有相对安全。

2.2 不同正态分布下的车流量与超车次数的关系

2.2.1 模型方法

为了研究速度上下限的控制对整个系统最佳放行量的影响，在上述模型的基础上增加一个变量，即改变速度的期望值来实现改变所抛出质点速度的正态分布形式，依次为X～N(33.3,4.822)、X～N(27.6,4.822)、X～N(23.68,4.822)、X～N(19.4,[4.822)]和X～N(16.6，4.822) 。

同理，使用C++进行模拟，并根据得出的统计量使用MATLAB 拟合、修匀，不同正态分布下的放行车辆与超车次数的关系如图5所示。

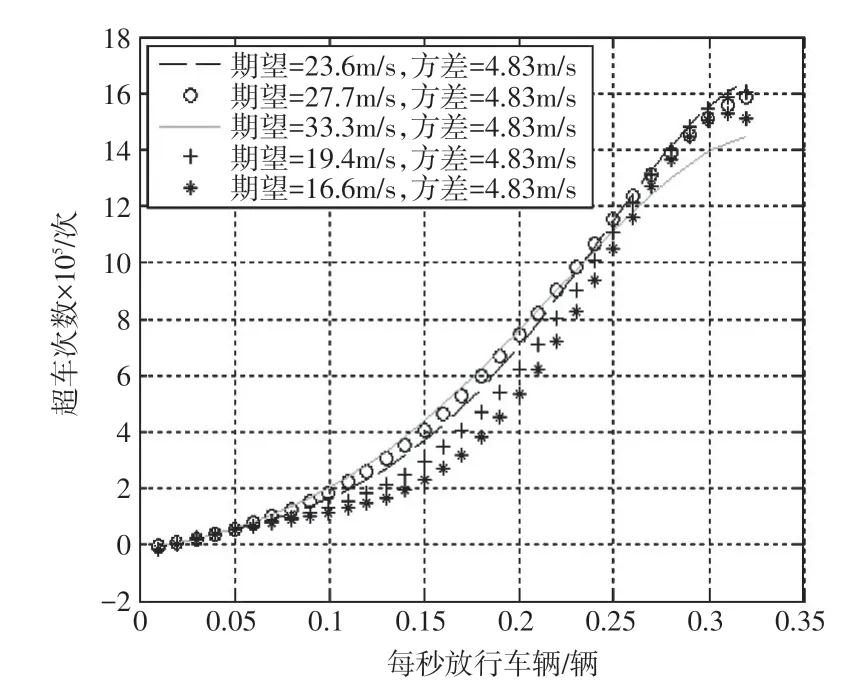
图5 不同正态分布下的放行车辆与超车次数的关系

2.2.2 模型分析

不同的车速控制下，曲线的形状并未发生巨大变化，依旧是先随着车流量的增大，超车次数缓慢增大；再经历一段快速走高的态势；最后，均在0.4veh/s后达到平稳。

模型函数的二阶导函数图像如图6所示。

图6 不同正态分布下的放行量与超车次数函数的二阶导数

基于上述最佳通行量的选择方法，X～N(33.3,4.832)、X～N(27.6,4.832)、X～N(23.68,4.832)、X～N(19.4,4.832)和X～N(16.6,4.832)的最佳通行流量依次为0.22veh/s、0.24veh/s、0.24veh/s、0.25veh/s 和0.25veh/s，所以行车速度的管制并没有太多的改变超车次数，这样就认为速度管制不会影响车流量。

考虑车流量和与超车率的关系：根据上述的文献资料可以知道车流量为860veh/h，即0.24veh/s时安全性越高，所以取0.24veh/s为相对较安全的车流量，这样就认为速度管制不会影响相对安全车流量。

2.2.3 模型结论

在安全和流量同时权衡时，可以以车流量为0.24veh/s为基础进行调整，调整量为0.01veh/s。所以控制流量在0.23～0.25veh/s 时交通更有效率且有相对安全。这样就得出：速度管制并没有有效提高车流量和安全度。

3 智能交通的超车模型实例

在实际道路中，超车与否不仅仅取决于车速，还取决跟车距离，以及个人的驾驶超车意愿等因素，而整个道路系统中，若其中某一辆车以上某一因素改变，必会导致后面车辆产生连锁反应，故不能简单地静态分析整个车道系统，同时由于动态分析会导致问题的连锁反应，也不宜采用此方法。在此，试图尝试从微观的角度考虑两辆车之间的超车行为，进而引进单辆汽车的智能驾驶，以构建整个智能的驾驶系统。

假设微观系统中，仅含两辆汽车，分别为前面的汽车A和后面的汽车B，且均服从右侧驾驶规则。首先由汽车B上的距离传感器检测出车A和车B 之间的距离，记为L，当L到达一个临界超车距离Lo时，开始考虑前后车速，这时前后车的车速由速度传感器测定，记前车车速为va，后车车速为vb，当va≥vb时，不考虑超车；但va＜vb时，才考虑从左侧超车。此时的系统开始进一步计算超车加速度这个过程中设定汽车有一个最大加速度amax，当a＜amax时，开始超车。当然，这个过程中还需检测A车的加速度aa，当aa＞0时，即前车处于加速阶段，给B车系统一个反馈信号，不允许B车超车，这也符合的法律规定；当aa≤0 时，开始考虑从左侧超车。这样微观智能汽车系统已经建成。对整体道路系统而言，系统是由很多无序的微观系统构成，当微观系统稳定时，智能道路系统也是稳定的，即此时道路系统可以正常运行。

4 结语

基于前两个模型的分析可知，在保证安全的前提下要使效率达到最高，可以以车流量为0.24veh/s为基础进行调整，调整量为0.01veh/s，即控制流量在0.23～0.25veh/s 时既可以使交通更有效率且有相对安全，同时速度管制并没有有效提高车流量和安全度。综上所述，在高速公路的匝道口日放行量每昼夜为39744～43200时既保证安全，又确保效率。

[1] 谭满春，徐建闽.车辆换道控制策略及其灵敏度分析[J].系统工程学报，2006（2）：206-210.

[2] 姚世华，谭满春.车辆换道与交通流多目标优化控制模型及算法[D].广州：暨南大学，2008.

[3] 荣建. 超车模型在双车道公路仿真系统中的应用研究[J].公路交通科技，2007（11）：136-139.

[4] 丁春雷.高速公路交通流数学模型与分析[D].天津：天津大学，2003.

[5] 阎莹，王晓飞.高速公路断面运行车速分布特征研究[J].中国安全科学学报，2008（7）：171-176.