分位数回归在大坝变形监测中的应用

袁国根

（江西省水利规划设计院，江西 南昌330029）

0 引言

大坝的变形受诸多因素的影响，如建筑物所在地的工程地质、水文地质、土壤的物理性质、大气温度等外部因素和建筑物承受的荷载、建筑物的结构、型式等内部因素。变形超过了规定的限度，会影响大坝的正常使用，严重时还会危及大坝的安全。因此，在大坝的施工和运营期间，必须对其进行变形监测和资料分析，为大坝的安全运营提供保障[1-2]。

在目前的大坝监测资料分析方法中，较为常用的有回归分析模型、灰色理论模型和混合模型等。但其中部分模型无法精确模拟出大坝的变形曲线，预测的结果精度较差，难以应用于实际工程中[3]。与传统的预测方法相比，分位数回归[4-9]以其高精度、高效及稳健的特点被广泛用于各类数据的预测计算中。本文利用分位数回归法对某大坝的垂向位移进行预测，并将预测结果与其他预测模型所得结果进行比较，结果显示分位数回归法预测精度更高。

1 分位数回归理论

设某随机变量y的分布函数为F（y）=P（Y≤y），y的分位数定义为：

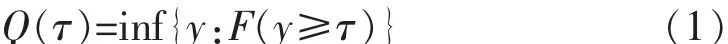
其中，0＜τ＜1，用Q（τ）表示y的分位数，当τ取 0.5时，即为中位数回归。

回归分析的基本思想就是使样本值与拟合值之间的差值最小，对于Y的一组随机样本，最小二乘回归是使误差平方和最小，即

式中，yi为样本值，ξ为拟合值。

而样本分位数回归是使样本与拟合值的加权误差绝对值之和最小，即：

从式（3）可以看出，分位数回归的算法就是最小一乘回归，当变形监测数据存在明显的异方差时，最小二乘估计就不再具有优良性质，稳健性表现差。而分位数回归具有单调同变性，对离群值不敏感，表现出很好的稳健性，估计出来的参数具有大样本数据理论下的渐进优良性，适用于大坝位移监测数据的预测。

2 实例分析

本文分析采用某土石坝垂向位移监测数据，现以某坝段施工后期2年左右的监测数据为例，以半个月为周期间隔共截取40期监测数据。为了方便后文的计算与分析，将40期数据分为两类：历史数据（前35期）用来建立分位数回归模型，检核数据（后5期）用来检验预测精度。

2.1 模型的确定

采用二次、三次、四次和五次模型结合4个具有代表性的分位数：0.3、0.5、0.7 及 0.9，利用 EVIEWS7.2 软件中的分位数回归功能对大坝垂向位移观测值进行回归分析。模型函数如下：

式中：βti为模型参数（t＝1，2，3，…，40，为观测数据的期数），n为模型次数，εt为误差项，相互独立，且εt～N（0，σ2）。

回归分析得到的结果是，四次模型的拟合精度最高，观测值和拟合值间的平均误差最小，其拟合效果和残差分别如图1和图2所示。

图1 四次模型各分位拟合结果图

图2 四次模型0.3分位拟合残差图

将后5期检核数据与四次模型函数的拟合结果作比较，如表1所示。从表1可以看出，四次函数在0.3、0.5、0.7、0.9 四个分位数下的拟合结果，以 0.3 分位下的拟合精度最高，误差绝对值之和的平均值最小为0.43。所以本文最终取四次模型在0.3分位时建立的分位数回归模型作为最终的预测模型。另外，从图1中沉降过程线和拟合过程线来看，该坝段沉降较为严重，因此在蓄水期和运行期间，应对该坝段垂向位移进行长期监测，并制定合理的防范措施，为大坝的安全运营提供保障。

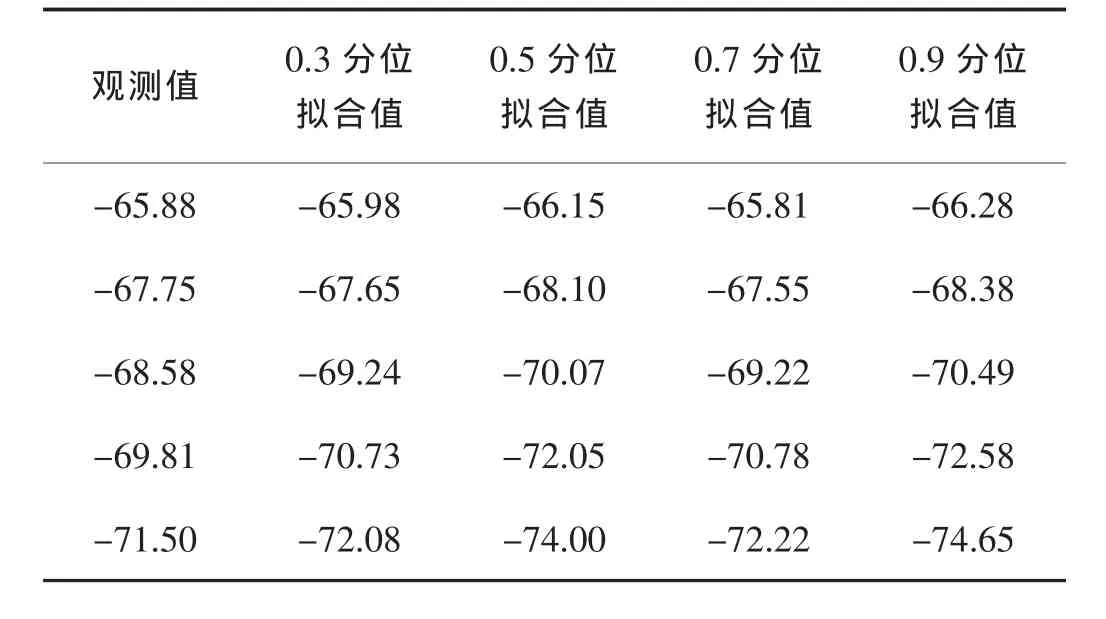
表1 四次函数各分位拟合结果

2.2 数据检核

为了检核分位数回归拟合结果的精度，用三次多项式结合最小二乘法以及一、二、三次指数平滑法对大坝垂向位移观测值进行预测，预测结果如表2所示。

表2 三次多项式及指数平滑法拟合结果

将各预测值与实测值的差值绝对值之和取平均后，与分位数回归分析的比较结果如表3所示。

表3 分位数回归和各预测方法平均误差比较

从表3可以看出，分位数回归的平均误差明显低于基于最小二乘的三次多项式拟合和一次指数平滑法，和二次指数平滑法和三次指数平滑法精度相当。

3 结语

本文介绍了分位数回归的基本理论和方法，利用EVIEWS 7.2软件对大坝垂向位移监测数据进行回归分析，确定最终的预测模型。并将分位数回归模型预测结果与多项式模型及指数平滑法预测结果进行了比较，结果表明分位数回归法预测精度理想，很好地反映了大坝的变形趋势。

［1］许 昌，岳东杰，董育烦，等.基于主成分和半参数的大坝变形监测回归模型［J］.岩土力学，2011，32（12）：3738-3742.

［2］吕蓓蓓，杨远斐.偏最小二乘法与神经网络耦合的大坝监测模型［J］.人民黄河，2013，35（3）：84-85，89.

［3］江 科.大坝安全监测数据分析方法研究［J］.科技资讯，2012，（35）：53-54.

［4］关 静.分位数回归理论及其应用［D］.天津大学，2008.

［5］李小辉.分位数回归理论及其在风险分析中的应用［D］.华北电力大学（北京），2013.

［6］张 利.线性分位数回归模型及其应用［D］.天津大学，2009.

［7］ 姜成飞.分位数回归方法综述［J］.科技信息，2013，（25）：185，240.

［8］陈雪蓉.复杂数据下分位数回归建模及其应用［D］.云南大学，2012.

［9］彭良玉.分位数回归在时间序列中的应用［D］.天津大学，2010.