数据分析在车间刀具及设备管理方面的探索

吴家兴 张海军 张新炜 王怡然 王洪峰 王 美

（内蒙古北方重型汽车股份有限公司 内蒙古包头）

一、前言

在精益管理推行之初，一项重要的工作就是各种管理数据的收集整理。机加车间作为精益工作的试点单位，于2013年正式开始记录车间的刀具消耗量、设备运行时间、工时数、设备故障次数、总停机时间等数据。经过17个月的数据收集，车间已掌握了一套具有参考性的管理数据。以所掌握的管理数据为基础，运用统计工具对其进行分析，探索数据背后的玄机。

首先，将所需要的数据进行整理。目前的数据统计可以覆盖到单台设备的月时段，本次选取车间2013年1月至2014年5月的58台设备数据为数据样本。其运行时间、工时数及故障次数见表1。

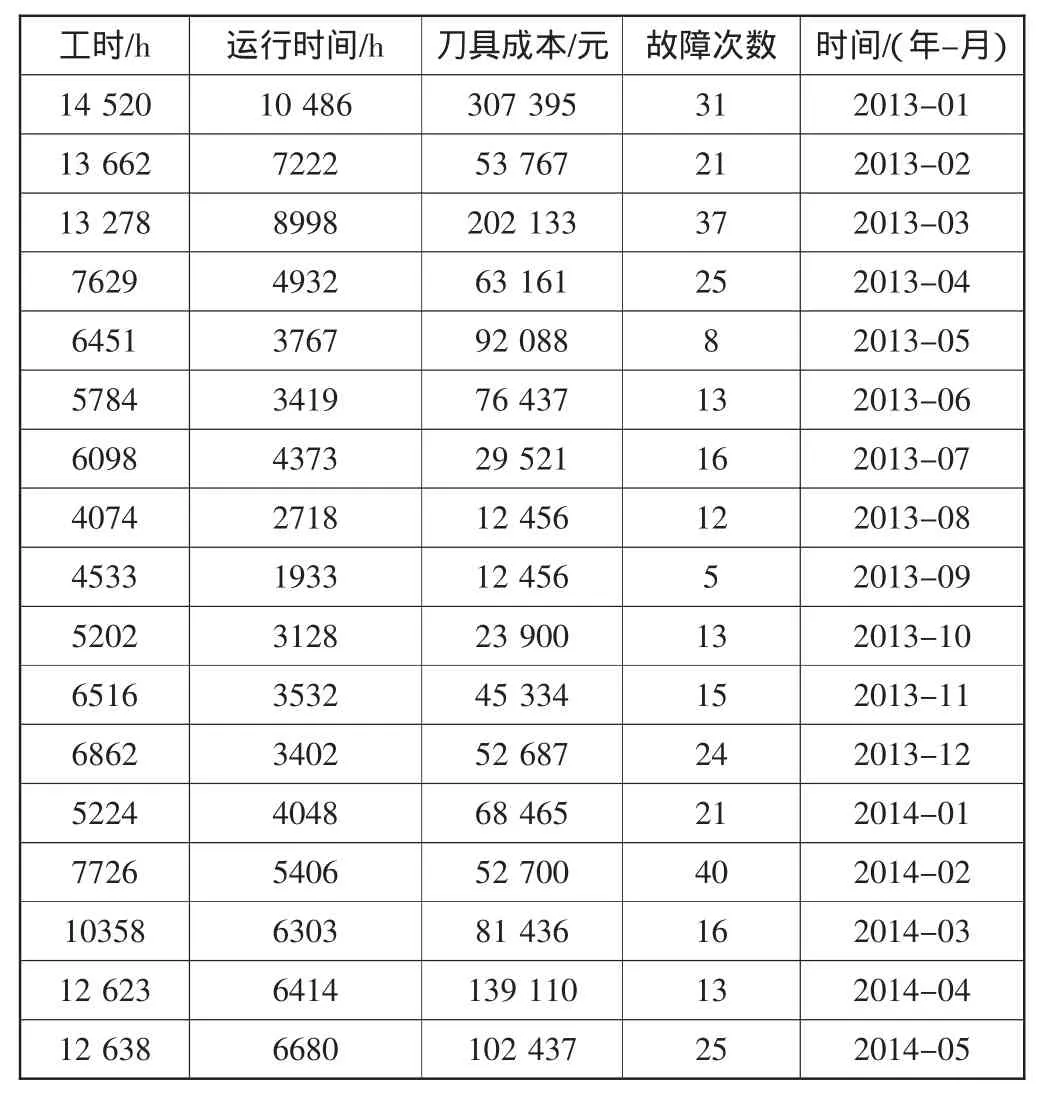
表1 机加车间2013年1月～2014年5月数据统计表

这些数据之间是否具有某些联系？数据背后是否隐藏着某些规律？下面运用统计工具大胆假设，小心求证。选用最小二乘法对数据进行回归分析。最小二乘法是利用已知数据点位与未知曲线方程误差的平方和为最小原理，利用对其最小值求各系数一阶偏导数为0的方法，求出回归方程的分析法。其具体计算过程，不再赘述。EXCEL作为出色的数据处理软件，可以非常方便的对数据进行回归分析。利用EXCEL的2013版进行回归分析。

二、工时与设备开机时间的关系探索

首先确定以ERP为主统计出的总工时与实际记录的设备开机运行时间的关系。横坐标为设备开机运行时间，纵坐标为总工时。分别使用线性回归、指数回归、二项回归对其对其分析，见图 1～图 3。

图1 线性回归分析图

图2 二次回归分析图

从相关系数R2及曲线趋势图来看，无论是哪种拟合都反映出数据间有强正相关性。结合数据特性分析，可得出结论，现有工时与机床开机时间具有线性相关性，线性回归方程约为y=0.61x+4.3

图3 指数回归分析图

三、设备运行时间与刀具消耗金额及故障次数间的关系探索

选取横坐标为设备开机运行时间，主纵坐标为刀具消耗金额，次纵坐标为故障次数，对其进行回归分析。A线为开机时间与刀具金额的回归曲线，曲线为二项式。回归系数为R=0.92，有强相关性。B线为假设的工时与效益的线性曲线，方程为y=200x（每工时创造200元效益）。C线为开机时间与故障次数的回归曲线，回归方程为三项式，相关系数R=0.68，见图4。

从回归曲线可以初步分析，设备的开机运行时间与故障次数及刀具消耗均不是线性关系。对回归方程分别求导可得：f＇（x）=0.0082x－22.275，方程在x=2716处出现拐点。设备的开机时间与故障次数回归方程求导f＇（x）=3×10－10x2-4×10-6x+0.0164拐点出现在8000左右。由方程和图像可近似得出以下结论。

（1）在加工量较少时刀具消耗较小，且消耗金额增长缓慢，但随着加工工时量的增加，刀具消耗金额将会大幅上升，并将在53 904 h运行时间处超越创造的效益（尽管这是不可能达到的），这可能是由于机床的某些特性造成的。

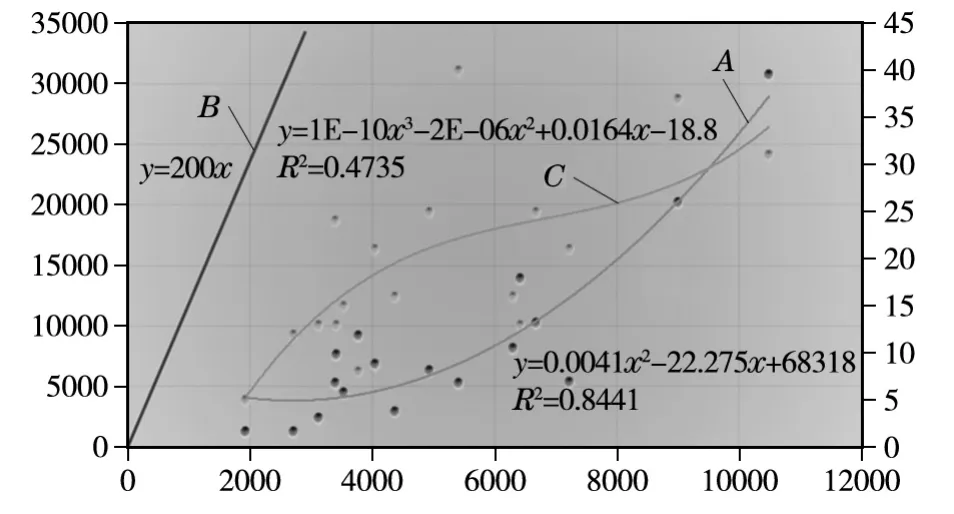
图4 多因素回归曲线

（2）故障次数增加率在设备运行时间2000～5000 h范围较大，但在5000～9000 h间放缓。这可能也是由于设备的某些特性造成的，当设备达到一定的稳定运转范围，故障反而不会上升，当超过某一临界值时，设备故障率才会大幅升高。

（3）在设备运行5000～8000 h的范围内，设备加工工时将同刀具消耗和故障次数取得一个相对较好的平衡，因此建议车间任务量尽量保持在这样一个范围内。

四、小数据分析的不足

以上所做的分析，仅基于17个月的数据，当然存在着不足和问题。

（1）数据的取得均来源于人为统计，与真值之间必然存在着差异，需要日后通过采用自动化及信息化统计手段，提高数据的准确性。

（2）数据样本为17个月的统计数据，样本相对较小，结论合理性仍需要长期观察检验。

（3）设备样本数据来源较杂，为50多台设备的综合数据，缺乏针对性分析，因此结论的合理性仍需细化分析。