锚杆对称分布形式对边坡稳定性影响分析

林 杭，陈宝成，钟文文

(1．西部灾害与环境力学教育部重点实验室(兰州大学)，甘肃兰州 730000;2．中南大学资源与安全工程学院，湖南长沙 410083)

全长粘结式锚杆安全可靠、施工简单、成本较低，在边坡工程中得到广泛应用。它能加固岩土体，并限制其变形，改善岩土体的力学参数及应力状态［1-4］。由于锚杆荷载传递机理较为复杂，许多学者通过数值计算方法研究锚杆与土体之间的相互作用。贺若兰等［5-6］研究锚杆工作机理时采用一种能够模拟锚杆和岩土体界面闭合、滑移及张开等实际变形性能的摩擦接触型界面单元;李青锋等［7］建立了预应力锚杆支护系统的动力分析模型。对于边坡来说，锚杆参数如长度、间距、倾角以及锚杆布置方式对于锚固效果、边坡安全系数以及滑动面位置都会有影响。彭文祥等［8-9］研究了锚杆长度、垂直间距、锚杆倾角、布设位置、锚杆直径和砂浆厚度对边坡安全系数的影响;万林海等［10］研究了安全系数及其灵敏度与土钉设计参数之间的变化关系;张钦喜等［11］计算了土钉和面层连接、土钉倾角、土钉长度布设、土钉间距4种因素对基坑变形的影响;林杭等［12］分析了锚杆长度变化对边坡安全系数和滑动面的影响以及锚杆的力学响应。这些研究的重点在于锚杆参数对边坡稳定性的影响，一般采用等长锚杆加固方式，而对于其他布设形式的锚杆则较少采用，使得设计结果过于保守。因此，本文通过数值模拟，利用双弹簧锚杆单元，采用强度折减法［13-14］进行边坡稳定性分析，研究锚杆的对称布置形式对边坡安全系数及滑动面位置的影响。

1 数值计算模型

边坡计算模型尺寸为:边坡高度20 m，坡角59°，按照平面应变问题建立数值模型。由于模型边界对计算结果存在一定影响，根据张鲁渝等［13］的建议，选取坡脚到左端边界的距离L=30 m，坡顶到右端边界的距离R=50 m，坡底到底端边界的距离B=20 m，模型尺寸比例如图1所示。

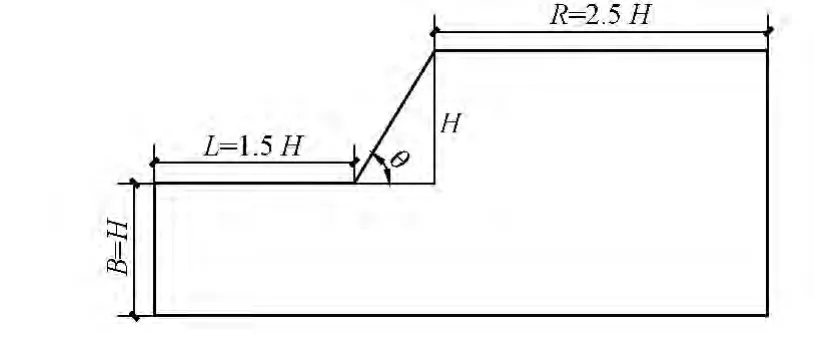
图1 边坡边界范围比例示意

考虑计算精度以及计算耗时，网格单元取1 m为划分单位，建立FLAC3D数值模型如图2所示。整个模型分3个部分建立，模型共包含3 080个单元，6 426个节点。模型边界约束条件为下部固定，侧向受水平约束，上部为自由边界。土体破坏符合Mohr-Coulomb准则，初始应力场按自重应力场考虑。计算过程中若不平衡力比率(节点平均内力与最大不平衡力的比值)＜10－5即认为系统达到平衡状态。边坡土体参数:弹性模量 E=100 MPa，泊松比 μ=0.3，重度γ=20 kN/m3，黏聚力c=40 kPa，内摩擦角 φ =18°。在未进行任何支护情况下，可计算得到边坡安全系数为0.96。

图2 FLAC3D边坡计算模型

采用FLAC3D中自带的双弹簧cable单元来模拟锚杆，该单元通过锚杆和岩土体之间的相对位移来模拟二者界面之间的力学行为。在数值计算过程中，通常将实际锚杆模型划分为大量的微单元，这些微单元本身满足经典力学理论，然后，通过微单元力学行为的积分效应，得到锚杆整体的应力和变形情况。为分析锚杆加固作用，设置锚杆参数为:钢筋直径30 mm，钢筋弹性模量 Eb=200 GPa，泊松比 μb=0.25，截面积706.5 mm2;注浆体直径100 mm，周长314 mm。注浆体与土体界面参数为:粘结刚度1.0×107N/m，砂浆黏聚力35 kPa，内摩擦角25°。

在距坡顶竖向距离2 m处打入第1层锚杆，自上而下共打入9层锚杆。为了分析锚杆用量不变情况下，锚杆的布设形式对边坡稳定性的影响，保持9层锚杆总长度为72 m，各层锚杆以8 m为长度标准进行增减，设置锚杆倾角为10°，竖向间距2 m。若锚杆为等长布置时，通过计算得到锚杆的有效锚固长度为20 m，因此，在设计计算工况时，锚杆的长度变化范围均小于有效锚固长度。

2 分析与讨论

当锚杆长度相对于中心锚杆(即本文中的第5层锚杆)对称分布时，将锚杆组合形式分为两类，以分析其对边坡安全系数的影响。

2.1 锚杆中间短两边长型布置

锚杆布置简图如图3所示，通过改变锚杆的长度，分析其对边坡安全系数的影响。

图3 锚杆布置

表1列出了各个工况中对应位置所有锚杆的长度。由计算所得的安全系数可知，当锚杆的长度变化时，边坡的安全系数基本保持不变。同时，由图4可以看出，边坡潜在滑动面的位置基本固定在同一位置，变化极小。

表1 锚杆中间短两边长型布置参数及安全系数

图4 锚杆中间短两边长型布置不同工况滑动面位置变化

图5为3种工况下锚杆与边坡滑动面位置的关系，可以看出，3种工况的上中层锚杆均未穿过滑动面，仅有少数下层锚杆穿过滑动面。为分析所有锚杆位置与边坡潜在滑动面的定量关系，以边坡坡脚为坐标原点，以边坡右侧方向为x向，竖直方向为y向，建立直角坐标系。通过自编程序得出边坡滑动面上点的坐标，利用二次多项式对滑动面曲线进行拟合，得到拟合方程。锚杆位置采用线性方程表示，通过计算可得到锚杆端部的位置坐标。同时联立锚杆及滑动面的位置方程可以求出二者的交点。计算锚杆端部与交点间的距离，即可得到锚杆沿其打入土体方向穿过(或未穿过)边坡滑动面的长度，从而确定锚杆与边坡滑动面具体的位置关系，分析二者相互作用的范围，得到不同位置锚杆对边坡稳定性的影响。

图5 中间短两边长3种工况下锚杆与滑动面位置的关系

由于边坡潜在滑动面的位置变化不太大，故将边坡3个滑动面简化为1个滑动面表示，采用二次多项式进行拟合，得到的拟合方程如下

式中，0≤x 且 y≤20。

拟合后曲线与边坡滑动面位置基本一致，再将锚杆在该坐标系下用方程定义，第i层锚杆位置方程为

式中:(x0，y0)为坡顶坐标;β为锚杆倾角;s为锚杆竖向间距;θ为边坡倾角。

通过计算求出各层锚杆端部穿过(或未穿过)滑动面的长度，结果如表2所示。计算结果与图5大体一致。

表2 中间短两边长型锚杆端部与滑动面位置的关系

由表2可以看出，3种工况中，上部7层锚杆几乎全部未穿过边坡滑动面，而下部第8，9层锚杆的长度总和从工况1到工况3有所增加，同时穿过边坡滑动面的距离总和略有增加，但对应的安全系数变化较小，分别为1.15，1.16和1.15，由此可以说明最底部穿过滑动面锚杆的长度对边坡安全系数的影响很小。对比工况2和工况3可知，当第8层锚杆穿过滑动面长度不变时，第9层锚杆穿过滑动面的长度增加对安全系数的提高没有贡献。这说明锚杆穿过滑动面锚固到未动土体中的锚固长度存在最优长度，本文中该长度在5～8 m。超过最优长度，继续增大锚杆长度对于边坡安全系数影响很小。

2.2 锚杆中间长两边短型布置

锚杆布置形式见图6，各工况参数及安全系数见表3。

图6 锚杆布置

表3 锚杆中间长两边短型布置参数及安全系数

由表3可知，当锚杆的长度变化时，即靠近中间锚杆长度加长，靠近坡顶和坡脚的锚杆长度减小，边坡的安全系数逐渐变大，分别为1.06，1.11和1.15。由图7可以看出，边坡潜在滑动面的位置较为固定，但是依然可以看出由工况4到工况5，边坡滑动面向坡内侧发展，而当变为工况6时，滑动面反而向临坡面靠近。

图7 锚杆中间长两边短型布置不同工况滑动面位置变化

计算求出各层锚杆端部穿过(或未穿过)滑动面的长度，结果见表4，其中包括锚杆长度、穿过滑动面锚杆长度等信息。

表4 中间长两边短型锚杆端部与滑动面位置的关系

由FLAC3D可以计算得到锚杆长度和边坡滑动面位置之间的关系，如图8所示。可以看出，除了工况5，6中间(第5层)锚杆穿过边坡滑动面之外，其余锚杆均未穿过滑动面。这与表4所示结果基本相同，3种工况中第5层锚杆穿过滑动面的近似长度分别为－1.3(表示未穿过滑动面)，2.7，6.7 m，同时边坡的安全系数分别为1.06，1.11，1.15，呈现逐步增加趋势。这说明在其他锚杆加固了整个滑坡体，形成钢筋土复合结构的同时，穿过滑动面的锚杆长度对边坡的安全系数影响较大。同时由于中部锚杆长度增加，坡顶和坡脚的锚杆长度减少，导致边坡下部加固土体范围变小，因此出现工况6中边坡滑动面向临坡面发展的现象。

图8 中间长两边短3种工况下锚杆与滑动面位置的关系

表5为两类锚杆组合形式对安全系数的影响，分析上下对称分布的两种形式，发现中间短两边长型比中间长两边短型锚固效果好。锚杆穿过滑动面的数量对边坡的安全系数有较大影响。锚杆穿过滑动面锚固到稳定土体中的锚固长度有最优长度，对于本文模拟的边坡，该长度为5～8 m，超过此范围后增加锚杆长度效果减弱。使用锚杆对边坡进行加固时，应适当增加中下部锚杆长度，使其穿过滑动面一定范围，提高边坡安全系数。中上部土体中锚杆长度可以适当减少，总体起到加固表层土体形成复合结构的作用，保证边坡不发生临坡面垮塌。

表5 两类锚杆组合形式对安全系数的影响

3 结论

1)在其他锚杆加固了整个滑坡体形成钢筋土复合结构的同时，穿过滑动面的锚杆长度对边坡的安全系数影响较大。

2)锚杆中间短两边长型布置比中间长两边短型布置锚固效果好。锚杆穿过滑动面的数量对边坡的安全系数有较大影响。锚杆穿过滑动面锚固到稳定土体中的锚固长度存在最优长度，超过此范围后增加锚杆长度效果减弱。

3)使用锚杆对边坡进行加固时，应适当增加中下部锚杆长度，使其穿过滑动面一定范围，提高边坡安全系数。中上部土体锚杆长度可以适当减少，总体起到加固表层土体形成复合结构的作用，保证边坡不发生临坡面垮塌。

［1］段建，言志信，郭锐剑，等．土层锚杆拉拔界面松动破坏分析［J］．岩土工程学报，2012，34(5):936-941．

［2］郭小红，王梦恕．隧道支护结构中锚杆的功效分析［J］．岩土力学，2007，28(10):2234-2239．

［3］何文，王成，王海菠，等．扭转导波在锚固锚杆中传播的数值模拟［J］．岩土力学，2011，32(4):1223-1228．

［4］康红普，姜铁明，高富强．预应力在锚杆支护中的作用［J］．煤炭学报，2007，32(7):680-685．

［5］贺若兰，张平，李宁，等．拉拔工况下全长粘结锚杆工作机理［J］．中南大学学报:自然科学版，2006，37(2):401-407．

［6］贺若兰，张平，刘宝琛．锚杆拉拔试验的理论和数值分析［J］．岩土力学，2006，27(增 2):855-859．

［7］李青锋，朱川曲，段瑜．预应力锚杆支护系统动力特征的数值模拟［J］．煤炭学报，2008，33(7):727-731．

［8］彭文祥，尹泉．土锚相互作用特征的数值实现方法及验证［J］．科技导报，2010，28(3):66-69．

［9］彭文祥，赵明华，袁海平，等．基于拉格朗日差分法的全长注浆锚杆支护参数优化［J］．中南大学学报:自然科学版，2006，37(5):1002-1007．

［10］万林海，余建民，冯翠红．软土复合土钉支护结构参数优化设计［J］．岩石力学与工程学报，2004，23(19):3342-3347．

［11］张钦喜，何建勇，霍达，等．土钉墙变形破坏的数值模拟及设计参数优化［J］．土木工程学报，2003，36(11):24-28．

［12］林杭，曹平．锚杆长度对边坡稳定性影响的数值分析［J］．岩土工程学报，2009，31(3):470-474．

［13］张鲁渝，郑颖人，赵尚毅，等．有限元强度折减系数法计算土坡稳定安全系数的精度研究［J］．水利学报，2003，34(1):21-27．

［14］赵少飞，栾茂田，吕爱钟．土工极限平衡问题的非线性有限元数值分析［J］．岩土力学，2004，25(增2):121-125．