数字分析法在消防统计中的应用

●赵步逵，刘东海

(武警学院 a．研究生队;b．消防指挥系，河北 廊坊 065000)

随着社会经济快速发展，我国每年由火灾所造成的财产损失和人员伤亡情况逐渐引起了社会各界的广泛关注。以火灾统计四项指标为主的消防统计数据质量的好坏直接影响着我国火灾安全形势的分析和未来公共消防政策的制定。同时，随着《中华人民共和国统计法》的修订实施和政府绩效评价的推广完善，消防统计数据的质量也不断受到社会各界的关注。数字分析法是以Benford定律为基础发展起来的一种根据数字分布规律来检测异常的方法，它具有操作简单，无需专业知识背景即可完成检测任务的优点。本文拟利用我国2011年消防统计数据进行实证分析，对如何运用数字分析法来检验我国消防统计数据质量做出一些探讨。

1 Benford定律的原理

Benford定律被称为“第一位数分布规律”，该定律揭示了海量数据中第一位数字出现的频率。通过对Benford定律中数字分布规律的应用研究，人们可以将Benford定律作为对统计数据进行质量检验的理论依据。在过去半个多世纪里，国内外学术界有关Benford定律的应用研究大部分都集中在财产审计和金融经济领域，在消防统计领域中关于Benford定律的应用研究还处于空白阶段。

2 Benford定律的应用

Benford定律要求被检测数据的第一位数字应该为有效数字，所以在进行实证检验时首先运用测试工具对所有需要检验的数字进行提取和整理，保证第一位数字符合非零、非负的原则然后对各个数字出现的频率进行计算分析。

2．1 测试工具

应用Benford定律在进行数据质量检验时可以借助计算机实现快速检验分析，通常各类统计分析软件，如Excel、SPSS、SAS都满足检验所需要的功能要求。考虑到Benford定律进行数据检验时需要提取各个数据的第一位数字，而Excel软件对这项操作更为简便易行，所以本文拟使用微软办公软件的Microsoft Office Excel的2003版作为数据处理软件。

2．2 测试方法

2．2．1 输入样本数据。将样本数据全部导入或者拷贝到Excel电子表格的第A列，假定共有1 000个数据。

2．2．2 整理样本数据。将数据拷入第B列，在B列中首先选择菜单中“升序排列”，将数据按照从小到大依次排列。通过观察，如果数据中有小于1的数据(如0．55)。可以直接在第B列第一行输入公式［B1*10］或［B1*100］。通过下拉菜单拷贝公式至数据最后一行，对整个数据样本乘以10或100(该项操作符合数据集比例不变性，篇幅所限不做赘述)。

2．2．3 截取样本数据的首位数。在第C列的第一行，设置函数［LEFT(B1，1)］并下拉拷贝公式至数据最后一行，电脑自动将第B列的首位数选出并存储显示在第C列。

2．2．4 计算首位数(1～9)的出现频数。在第D列的第n行输入公式:［COUNTIF(Cn:C1000，n)］;电脑就会自动在第D列出现样本首位数字1～9的出现频数。

2．2．5 计算首位数(1～9)出现的频率。在第E列第一行输入公式［D1/1000］，下拉拷贝公式到第9行，在第E列中就会依次出现首位数(1～9)出现的频率。

2．2．6 与Benford定律分布的比较。在第F列的前9行中输入Benford定律的期望分布概率，在第G列的第一行中输入公式［=E-F］，求得所检验的数据分布和Benford定律分布的差异值。

2．2．7 进行检验。通过 Excel软件的统计函数Pearson函数可以计算出相关系数的数值。

3 实证分析

3．1 数据来源

本文以公安部消防局编制的《中国消防年鉴》(2012)［1］中 2011年我国 31个省、自治区、直辖市(不包含新疆生产建设兵团)的火灾起数、火灾直接损失(万元)和火灾烧毁建筑(m2)这三类重点统计数据为实证分析的样本。消防统计数据中没有最大值和最小值的限制，也不存在人为赋值的影响，符合Benford定律的检验要求。为保证分析过程的准确性，对以上样本数据进行整理，剔除含0的数据4条，共得到有效数据1 415个，基本可以满足Benford定律对数据集规模的要求。

3．2 第一位数字

将样本数据按照火灾起数、火灾直接损失(万元)和火灾烧毁建筑(m2)划分成三项统计数据。其中火灾起数包含473个数据，火灾直接损失(万元)包含471个数据，火灾烧毁建筑(m2)包含471个数据。运用Excel软件求出上述三项统计数据中第一位数字的个数和频率(精确到0．000 01)，然后将各项统计数据的数字频率与Benford定律中第一位数字分布的频率在一起进行观察比较，如图1所示。可以看出，火灾起数，火灾直接损失(万元)和火灾烧毁建筑(m2)三项统计数据的第一位数字频率分布基本与Benford定律的第一位数字频率分布相一致，所存在的差别是否显著还需要进行进一步检验分析。

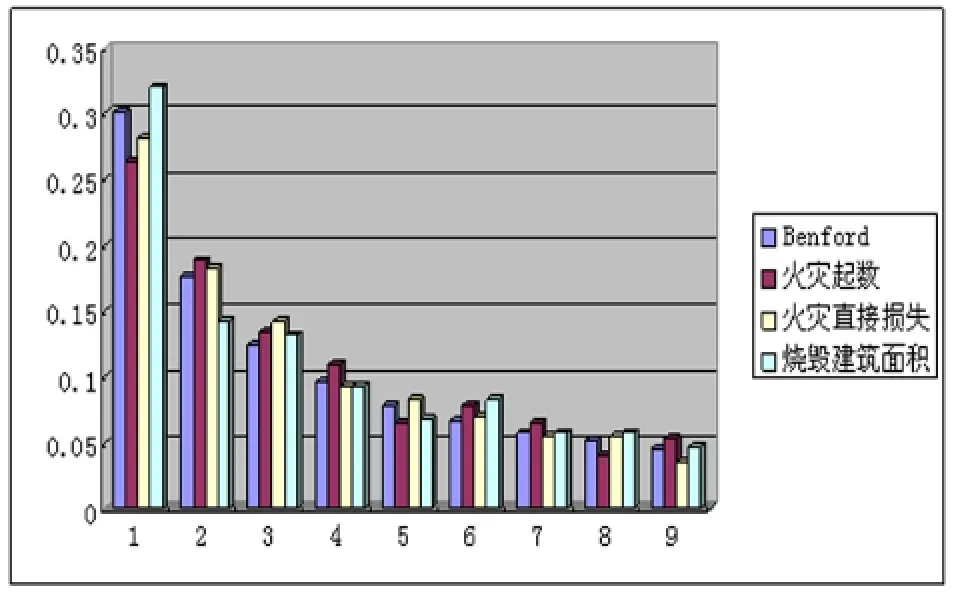
图1 三项统计数据与Benford定律的频率分布3．3 检验分析

本文采用Pearson相关系数进行检验分析，Pearson相关系数是用来反映两个变量线性相关程度的统计量，公式如下:

式中，r表示相关系数，描述的是两个变量间线性相关强弱的程度。r的取值在 －1与+1之间，绝对值越大表明相关性越强。若r﹥0，表明两个变量是正相关;若r﹤0，表明两个变量是负相关;若r=0，表明两个变量间不是线性相关［2］。

本文通过计算2011年我国火灾起数、火灾直接损失(万元)和火灾烧毁建筑(m2)的统计数据中第一位数字频率分布与Benford定律的期望频率分布的Pearson相关系数，来判断这三项统计数据与Benford定律分布之间是否存在显著差异［3］，判断标准见表1。

表1 Person相关系数的判断标准

通过Excel软件计算，上述三项统计数据的Pearson相关系数检验结果如表2所示，可以看到各项统计数据的Pearson相关系数都在0．98以上，基本可以认为2011年我国消防统计数据中火灾起数、火灾直接损失(万元)和火灾烧毁建筑(m2)的数据质量较好，不存在明显的可疑情况。但是在三项统计数据中除了火灾直接损失(万元)的Pearson相关系数大于0．99，表现为完全符合Benford定律，其余两项统计数据的Pearson相关系数都在0．98左右，也就是说火灾起数和火灾烧毁建筑(m2)的统计数据质量需要我们加以关注，对这两项统计数据还要进一步分析确认。

表2 统计数据检验结果

4 结论

我国每年的消防统计数据种类较多，覆盖范围较大，随着国家经济快速发展，各个地区的消防统计数据也呈现出不同的变化。这也是要寻找一种能够对我国消防统计数据质量进行快速简便分析的重要原因，本文经过实证研究，表明Benford定律可以较好的满足上述要求。在数据质量检验中引入Pearson相关系数进行数据分析，通过验检结果应该相信《中国消防年鉴》(2012)所公布的2011年全国31个省、自治区、直辖市(不包含新疆生产建设兵团)的火灾起数、火灾直接损失(万元)和火灾烧毁建筑(m2)的统计数据可靠性较高，没有明显的质量问题。

［1］公安部消防局．2012中国消防年鉴［M］．北京:中国人事出版社，2012．

［2］程广华．利用 Benford定律在海量数据中筛选非法商户研究［J］．探索论坛，2010，(4)．

［3］许存兴，王大江，张芙蓉．上市公司审计意见实证分析——基于Benford定律的造假检测［J］．南京大学财经学报，2009，(4)．