突发事件谣言传播的涌现模型与仿真研究

刘军光 欧微，2

(1.乌鲁木齐民族干部学院，新疆 乌鲁木齐830002;2.国防大学 信息作战与指挥训练教研部，北京100091)

1 引言

当前，我国已步入经济和社会转型期，各种不安定因素增多，各种突发事件的发生频率和社会破坏力不断增加。突发事件会引发高度的社会关注，在信息传播过程中容易出现消息失真、舆论失实的情况，加之部分民众的主观猜测与恶意关联，致使谣言比平时更容易滋生、感染和传播。谣言的肆意扩散容易引发社会心理恐慌和非理性反应，造成比突发事件本身更严重的后果，将严重影响民众生活与社会稳定［1，2］。

为探索谣言的产生机理、传播规律和消解对策，国内外学者对谣言传播模型进行了深入的研究。其中，最具代表性的谣言传播模型主要有两种:一是基于传染病的疾病传播模型，该模型将人群中的个体抽象为三类，分别对应三种典型状态，即易染状态S(Susceptible)、感染状态I(Infected)和免疫/移除状态R(Removal)［3，4］;另一种谣言传播模型基于Agent 建模思想，构建底层个体的微观模型，通过个体的行为模式和交互作用，模拟谣言传播的扩散过程［5，6］。由于传播机理的相似性，现有谣言传播模型大都借鉴了疾病传播模型，但该类模型的微分动力学方程是根据数理统计建立的，属于宏观数学模型，不能反应出微观个体相互作用对谣言传播的影响。基于Agent 理论的谣言传播模型，符合复杂系统的客观规律，通过模拟底层个体的行为模式和交互作用，可较好地涌现谣言传播的整体态势，但目前很少有文献关注个体的受教育程度、社会影响力、个体记忆机制等对谣言传播的影响。

本文在现有模型基础上，将疾病传播SIR 模型与基于Agent 的建模思想相结合，主要对模型进行了两点改进:一是考虑了个体差异对谣言传播的影响，即由于个体的受教育程度和社会影响力不同，其对谣言的质疑程度、传播概率、影响因子、社会关注度等均不尽相同;二是引入个体记忆机制，在交互过程中，记录个体接触谣言或事实的次数，其接触谣言(事实)的次数越多，则转变为感染(免疫)状态的概率将越大，从而更符合谣言的渗透与扩散规律，增强了模型的可信性与科学性。通过仿真实验，研究谣言的传播与消解规律。

2 谣言传播模型

在病毒传播SIR 模型的基础上，针对谣言传播人群中微观个体的属性特点和行为模式，采用基于Agent 的建模方法，构建微观个体的仿真模型，通过模拟微观个体的行为模式以及个体间的相互作用，涌现谣言传播的整体态势，进而研究谣言传播的扩散规律与消解对策。

2.1 模型假设

在现实世界中，个体之间的差异永远存在，且个体对过去的状态存在一定的记忆。因此，在研究谣言传播规律时，若对模型过于简化，忽略个体之间的差异和个体对过去状态的记忆，虽然降低了建模与计算难度，但会大大影响模型的科学性与可信性。在谣言传播过程中，个体差异特别是在社会影响力和受教育程度等方面的差异，会使得个体的质疑因子、传播概率、影响因子和社会关注度等均存在差异，从而造就个体间影响的不对等性;而个体记忆，则反映了个体在过去交互过程中接触谣言或事实次数对个体调整自身状态的影响。

为此，对模型作如下假设:

假设1 个体的质疑因子、传播谣言概率、传播事实真相的概率均与其受教育程度相关。

记个体的质疑因子为QF、传播谣言的概率为SP、传播事实的概率为TP，对应受教育程度高、中、低三个层次，将相应个体对应的属性(QF，SP，TP)的取值分别约定为(0.9，0.5，0.9)、(0.7，0.7，0.7)和(0.5，0.9，0.5)。即个体受教育程度越高，则对待谣言更为理性，其质疑因子将越高，传播谣言的概率将越低，而当其转变为免疫个体后，该个体向其他个体传播事实的概率也将会越大。

假设2 个体的社会影响力由影响因子和社会关注度构成，影响因子决定了其他个体与该个体交互时受影响的程度，而社会关注度则决定在单位时间内与该个体交互的个体数。

记个体的社会影响因子为IF，社会关注度为SA。将社会影响力划分为很高、高、中、低四个层次，将对应属性(IF，SA)的取值分别约定为(1.0，20)、(0.8，5)、(0.4，2)、(0.1，1)，即社会影响力较高的个体，其相应的影响因子和社会关注度也越高。需指出的是，在上述假设中属性值的大小只是根据某次仿真实验的需要设定的，在仿真过程中，可根据实际情况进行修订。

2.2 传播规则

在谣言传播仿真系统中，底层个体的行为模式和个体间的交互是实现宏观谣言传播整体态势涌现的基础，对谣言传播规则作如下约定:

规则1 随着个体听闻谣言的次数增加，其对谣言的质疑程度将逐渐降低;当个体接触事实的次数增多，其转变为相信事实的趋势将随之增加。

假定Agenti接触谣言的次数为NHR，接触到事实的次数为NHT，其质疑因子为QF，其态度向相信谣言的转换趋势为TR，则TR的计算公式为:

个体态度向相信事实的转换趋势为TT，则TT的计算公式为:

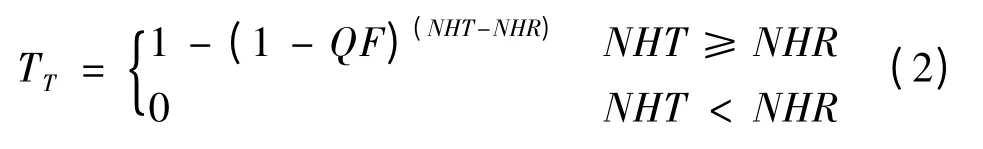
规则1 用于处理个体记忆对个体对待谣言态度转变的影响，即当个体在过去时间内接触谣言或事实的次数越多，则其向相信谣言(事实)转变的概率也将随之增加。

规则2 当易感个体与已感染个体接触，易感个体将以一定的概率转变为感染状态。

假定AgentA为易感个体，AgentB为已感个体，则当AgentA与AgentB交互，AgentA将以概率PIA转变为感染个体，转换概率PIA计算公式为:

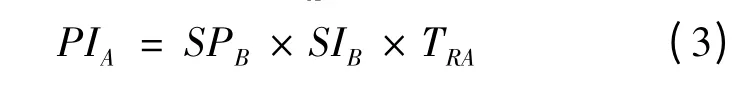
式(3)中，TRA为AgentA态度向相信谣言转换的趋势，由式(1)计算得出;SPB和SIB分别为AgentB的传播谣言概率与影响因子。

规则3 当易感个体或感染个体与免疫个体接触，则他们将以一定的概率转变为免疫状态。

假定AgentA为易感个体(或为已感染个体)，AgentB为免疫个体，则当AgentA与AgentB交互，AgentA将以概率PRA转变为感染个体，转换概率PRA计算公式为:

式(4)中，TTA为AgentA的态度向相信事实的转换趋势，由式(2)计算得出，SIB和TPB分别为AgentB的影响因子和传播事实的概率。

2.3 仿真计算流程

仿真计算的主流程如下:

(1)参数设置。设置个体数量Popsize、初始时感染个体数NI、初始时免疫个体数NR、最大仿真步数MG、个体间信任系数Trust、群体受教育程度分布和社会影响力分布情况等参数。

(2)模型初始化。按照模拟人群受教育程度分布、社会影响力分布等参数要求，随机生成Popsize个个体，按规则计算个体的社会影响因子、受关注度、质疑因子等属性，构成初始模拟人群。

(3)个体交互。在模拟人群中依次取出各个个体，若Agenti的社会关注度为SAi，则从人群中随机取出SAi个个体，按照谣言传播规则，Agenti依次与其进行交互，计算交互效果。

(4)终止准则。判断是否达到最大仿真步数MG，若是则退出程序，输出仿真结果，否则仿真步数加1，返回(3)继续运行。

3 仿真研究

利用C#编程语言编程实现突发事件下谣言传播仿真系统，然后在该平台上进行仿真研究。参数设置如下:个体数量Popsize =10000，初始时感染个体数NI =10，最大仿真步数MG =400，信任系数Trust =0.7，人群受教育程度高、中、低比例分别为0.2、0.6 和0.2，社会影响力很高、高、中、低比例分别为0.005，0.095，0.5 和0.4。

3.1 初始时无免疫个体、不进行干预

假定模拟人群中初始时免疫个体数NR =0，即初始时不存在任何免疫个体，且自始至终均不采取干预手段，仿真运行结果如图1 所示。

图1 初始时无免疫个体、无干预措施

其中，Susceptible 表示易感人群，Infective 表示已感染人群。由图1 可见，初始时谣言的传播速度较慢，但当时间推进到第85 步左右，谣言开始快速扩散，最后几乎整个人群都变为感染者。这是由于初始时感染个体数目较少，谣言只在小范围内传播;但随着时间推进，感染个体逐渐增加，个体接触谣言的概率和次数也将逐渐增加，因而产生了倍增效应，谣言得以快速扩散。

3.2 初始时有少量免疫个体、不进行干预

假定初始时免疫个体数NR =5，且仿真开始后不采取干预手段，仿真运行结果如图2 所示。

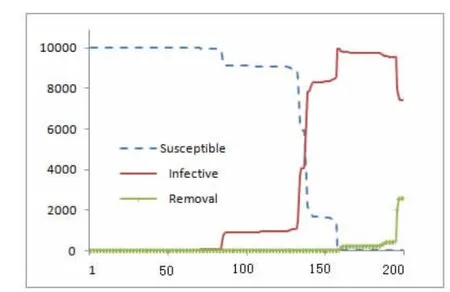
图2 初始时存在少数免疫个体、无干预措施

由图2 可见，谣言扩散的趋势与图1 大致相同，但谣言扩散速度相对缓慢一些，而当推进到第160步左右，免疫人群开始逐步增加，到第200 步左右，免疫人群有明显上升的趋势。这是由于有少量免疫个体的存在，在谣言扩散的同时他们将向与其他个体传播真相，从而延滞谣言扩散的速度，随着时间推移，感染个体接触事实的次数将逐步增加，致使转变为免疫个体的概率逐渐上升。

3.3 随机选择部分个体进行干预

假设初始时免疫个体数NR =0，当仿真运行到100 步，在模拟人群中随机选择20 个个体，将其强制转变为免疫个体后，再投放到人群中，继续进行仿真。

图3 随机选择部分个体进行干预

由图3 可见，在采取干预措施后，人群中的免疫个体开始时增长比较缓慢，当运行到第130 步左右，免疫个体数开始明显增加。这是由于在干预初期，由于免疫个体随机分布在社会影响力和教育层次各异的人群中，部分免疫个体对其他个体施加的影响有限，因而免疫人群增长的速度缓慢;而随着免疫个体的数目逐步增多，个体接触真相的概率和次数也逐渐增加，免疫人群的数量得以快速增长。

3.4 针对具有特定社会影响力的个体进行干预

条件设置与3.3 节基本一致，但实施干预的个体不再从整个人群中随机选择，而是分别从社会影响力很高、高、中、低四个层次的个体中随机选择，针对筛选条件不同，分别进行四组实验，仿真结果如图4 所示。

图4 针对特定社会影响力的个体进行干预

其中，VeryHigh、High、Middle 和Low 分别表示针对社会影响力很高、高、中、低四个层次的人群进行干预时，分别进行仿真实验，免疫个体数的增长曲线。由图4 可见，在实施干预后，免疫个体的数量均出现了不同程度的增长。其中，对社会影响力很高的人群进行干预后，免疫个体出现增长的速率最快，随着社会影响力递减，免疫人群的增长速率依次减慢。这说明，在谣言出现后，有针对性地对社会影响力较高的个体进行干预，再由他们进行舆论宣传，可起到较好的引导效果。

3.5 针对不同受教育程度的个体进行干预

条件设置与3.3 节基本一致，但实施干预的个体并不从整个人群中随机选择，而是分别从受教育程度高、中、低三个层次的个体中随机选择，针对筛选条件不同，分别进行三组实验，仿真结果如图5 所示。

其中，High、Middle 和Low 分别表示针对受教育程度高、中、低三个层次的人群进行干预，免疫人群的增长曲线。由图5 可见，在实施干预后，免疫个体的数量都有不同程度的增长，实施干预的个体受教育程度越高，免疫人群增加的速度越快，反之则越慢。这说明，在谣言出现后，有针对性地对教育程度高的个体进行干预，再由这些个体传播事实真相，也可取得较好的舆论引导效果。

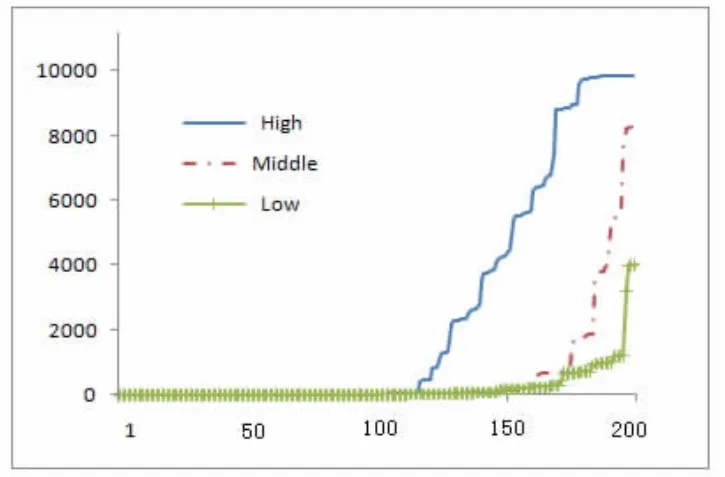
图5 针对特定受教育程度的个体进行干预

4 结束语

本文将传染病传播SIR 模型与基于Agent 的建模思想相结合，构建谣言传播仿真模型，开发谣言传播仿真系统，并进行仿真研究。仿真结果表明，当群体中存在免疫个体时，他们在交互过程中试图引导其他个体转变为免疫个体，使谣言逐渐趋于消解，特别是当这些个体的社会影响力和受教育程度较高时，谣言的消解速度将明显加快。突发事件发生后，谣言的肆意传播会严重影响民众生活与社会稳定。因此，在谣言出现后，应尽快发布事实真相，进行舆论引导，特别是针对社会影响力和教育程度较高的人群，应尽早加强宣传教育，使其在舆论宣传和谣言控制过程中发挥积极作用。

［1］ 赵玉忠，陈业华.谣言传播规律以及对群体事件的影响［J］.社会科学家，2012(8):37 -40.

［2］ 唐小青，李学军.重大突发事件中谣言传播的心理因素分析［J］.理论与改革，2013(5):152 -154.

［3］ RABAJANTE J，UMALI R E. A Mathematical model of rumor propagation for disaster［J］. Journal of Nature Studies，2011，10(2):61 -70.

［4］ 苏国强，兰月新. 基于SIR 的突发事件网络谣言扩散模型研究［J］.武警学院学报，2013，29(4):90 -92.

［5］ 阮冰，朱建冲，姜礼平，等. 复杂网络上的舆情形成演化建模与仿真研究［J］.军事运筹与系统工程，2010，24(1):53 -58.

［6］ 张芳，司光亚，罗批.基于演化博弈理论的人际谣言传播仿真模型研究［J］.系统仿真学报，2011，23(9):1772 -1775.