基于数字水印的无参考图像质量评估方法的研究
张 彪杨炳恒陈 强韩 玉
(1.中国人民解放军海军航空工程学院青岛校区光学引导与监控教研室,山东 青岛432400;2.中国人民解放军海军航空工程学院青岛校区教学科研办,山东 青岛432400)
0 引言
网络的发展促使网络多媒体业务的兴起。在图像传输系统中,需要根据信道条件实时调整压缩参数,从而提高用户的可感知质量,这就需要获得压缩和传输后的图像质量,从而自适应的控制编码端参数,达到提高系统整体质量的目的。因此研究对数字图像质量进行评估的方法一直备受关注。
数字图像质量评价方法[1]通常分为两大类:主观质量评估(SQA)和客观质量评估(OQA)。主观质量评估是直接由观察者对图像质量进行主观评价,此方法最为准确,但是需要提供严格的测试环境,实现起来步骤复杂、实时性差,不便于实时传输中图像质量的评估。客观质量评估[2]通过对图像序列进行一定的处理,根据所得到的信息作出评价,该类方法相比于主观质量评测方法更易于实现。根据对原始图像的依赖程度,客观质量评估又可以分为三类:全参考方法、部分参考方法、无参考方法。全参考和部分参考方法需要提供原始图像的全部或者部分特征和信息作为评价参考,而无参考方法则无需原始图像的任何信息。在图像的压缩和传输过程中,考虑到信道带宽,往往无法实时获取原始图像信息,所以无参考质量评价方法具有较高的应用价值,对其的研究也是目前学术界研究的热点之一,利用数字水印对图像质量进行评价正是无参考质量评价方法的一种。
1 原理及算法
1.1 基本原理
图像数字水印[3]是在原始图像数据中按照一定的规律嵌入另一种信号(水印)。由于图像数据存在的冗余,且人眼对图像中不同部分感知能力是不同的,因此可以利用这些特性在图像中嵌入水印,同时又不影响人眼对图像的主观感受——不可见性成为衡量数字水印嵌入算法的一个重要指标。图像中嵌入信号量越多,图像质量下降越明显,水印的不可见性越差;但是经过攻击后提取出来的水印质量会较好,即水印的鲁棒性较好。因此水印的不可见性和鲁棒性二者是矛盾的,相互制约。如何平衡水印嵌入的强度(鲁棒性)和嵌入后图像质量(不可见性)成为数字水印技术的关键[4]。
DCT域水印[5]能够较好地平衡上述问题,是目前数字水印研究的热点。DCT变换把空域信号变换到频域中一个DC分量和一系列的AC分量,其中,DC分量表示原始图像平均亮度,AC分量的每个系数均表示原始图像在某一个频率上的能量。经过DCT反变换后,DC和AC系数中的各个频率所表征的能量将均匀分配到原始图像的各个系数中。对单个DC或AC系数的修改将会分散到原始图像的各个像素值,从而避免了对原始图像的某几个像素值进行修改所导致的大幅度失真,水印的鲁棒性和不可见性都得到保证。但是在DCT域进行水印嵌入需要首先对原始图像进行DCT变换,嵌入水印后再对图像进行反变换,算法复杂度较大。考虑到JPEG压缩[6]时,必须对图像进行DCT变换后再进行量化和熵编码,因此可以将水印嵌入过程和图像压缩过程相结合,从而节省计算量。
本文提出的算法其基本思想为:在图像压缩过程中,首先对图像进行DCT变换,在变换后的系数中嵌入水印信息;所得到系数再经过量化和熵编码得到压缩码流,通过信道传输至解码端。解码端获得压缩码流后,经过熵解码,反量化后得到DCT系数,从中提取出水印信息。将提取出的水印与原始水印进行比较,得到提取水印的图像质量,再利用水印质量与图像质量之间的关系式得到图像质量。由于嵌入的水印与原始图像一样经历了量化和信道误码等导致图像质量损失的过程,因此水印信号与图像信号的受损程度之间是有着较大的关联的,可以通过提取出的水印质量获取图像质量。
1.2 水印嵌入算法
这里选择要嵌入的水印为二值水印,二值水印中图像像素只有“0”和“1”,与数据的奇偶性可以相互对应。即“0”表示偶数,“1”表示奇数。因此,可以通过判断DCT系数均值的奇偶性,与水印对应位的奇偶性相同时,则不需要修改DCT系数。否则,通过对DCT系数作相应的修改,从而达到修改均值奇偶性的目的。具体的水印嵌入算法如下:
第一步:将二值水印图像转变为二进制串;
第二步:将原始图像进行8×8分块的DCT变换;
第三步:利用随机数发生器,生成随机数向量,并将其按从大到小的顺序进行排序。通过此方式获得与排序后随机数相对应的位置向量,并选择与二值水印长度相同的前n个位置,作为水印嵌入块的序号;
第四步,对每个8×8的水印嵌入块分别进行DCT变换;接着将DCT系数按照Zig-Zag(如图1中Zig-Zag排列图)排列;求预先定义的所选频率系数和的奇偶性,然后与二值水印(0或1)做比较,如果相同则不做修改;如果不同,则改变DCT系数值;这样分别将二值水印二进制串嵌入到源图像的DCT块中。

图1 Zig-Zag排列图
水印的嵌入公式:

其中d为量化因子(通过改变d的大小可以控制水印的嵌入强度),ROUND为取整函数(四舍五入),I为DCT系数,I′为变换后的DCT系数。值得注意的是,上述水印嵌入算法仅针对Y分量进行嵌入,对U,V两分量是没有影响的。
1.3 水印提取算法
第一步:接收压缩后的载体图像,读取载体图像;
第二步:将二值水印图像转变为二进制串;
第三步:利用随机数发生器,生成随机数向量,并将其按从大到小的顺序进行排序。通过此方式获得与排序后随机数相对应的位置向量,并选择与二值水印长度相同的前n个位置,作为水印提取块的序号;
第四步:对每个8×8的水印嵌入块分别进行DCT变换;接着将DCT系数按照Zig-Zag(如图2.1中Zig-Zag排列图)排列;求预先定义的所选频率系数和的奇偶性。如果为偶数,则提取水印对应位为“0”,否则提取水印对应位为“1”。
从上面的水印嵌入和提取算法可以看出,量化因子d控制着水印的嵌入强度,随着量化因子d的增大,图像质量变差,水印图像明显;而当d变小时,水印易受到攻击,提取出的水印无法表征原始图像质量,必须要选择合适的d值。另一方面,DCT系数经过Zig-Zag扫描后,靠前的系数属于中低频系数,人眼对其较为敏感,而靠后的系数属于高频系数,人眼对其不敏感。选择在低频系数中嵌入水印能够提高水印的鲁棒性,提取出的水印也可以较好的表征图像质量,但是将对图像质量造成较大的影响;而选择中高频系数嵌入水印,水印不可见性较好。但是在图像量化的过程中,由于中高频系数值一般较小,大部分的水印将随着高频系数被量化为0,水印鲁棒性降低。因此需要确定合适量化因子d的取值以及在哪些频率系数中嵌入水印,在本文后续章节中将逐一对这些问题进行分析。
2 确定量化因子与水印嵌入区域
2.1 量化因子d取值范围
本节将通过实验分析量化因子对图像质量造成的影响,为了屏蔽压缩所带来的图像失真,将不对图像进行压缩。通过改变量化因子d,观察提取水印相对于原始水印的错误率(BER)变化情况和图像峰值信噪比(PSNR)的变化情况;然后比较两者随d增大而改变得到的曲线,分析两条曲线变化趋势,然后为d选择合适的取值范围。由于还未确定具体在DCT哪些系数中(后面均用range_dct表示要嵌入水印的DCT系数位置)嵌入的水印下,本实验在中频、低频、中低频三种情况下嵌入水印。实验结果表明,上述三种嵌入策略嵌入水印后的BER曲线和PSNR曲线的变化趋势基本都是相同的,因篇幅限制,在此仅给出在DCT低频嵌入水印时的实验结果。
实验中所采用的载体图像为标准测试图像Lena,其幅面大小为512×512。图1(a)表示按照Zig-Zag扫描顺序在第2、3、4、5、6、7、8、9、10位嵌入水印,记为range_dct=2:10。(b)图表示在第4、5、6、7、8位嵌入水印,记为range_dct=4:8。
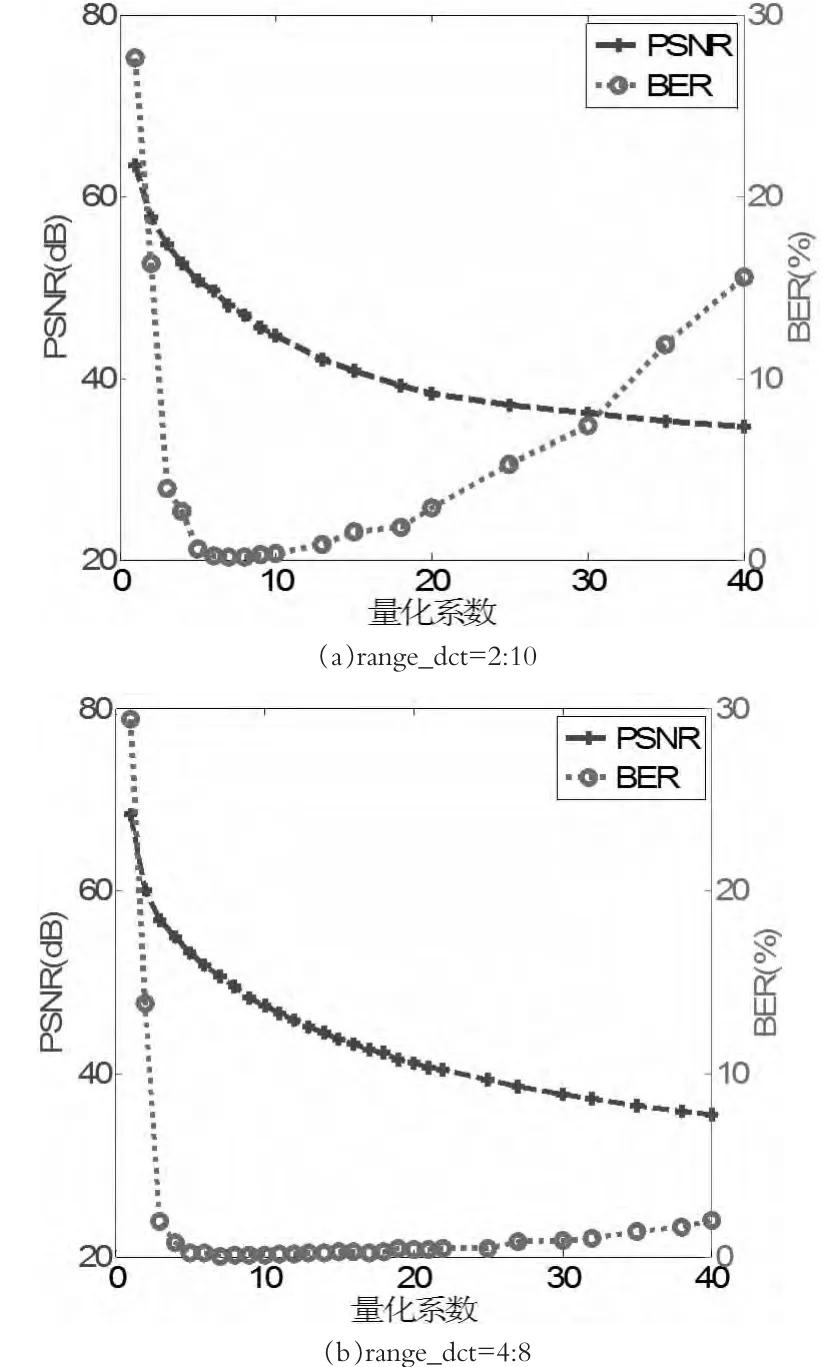
图1 DCT低频位嵌入水印
由图1可以看出,d的取值在5~6这一范围时,提取水印的BER是最小的,而PSNR又保持在大于50dB的范围内。因此d的取值为5或6是最可取的,而考虑到在图像压缩比较大的情况下会导致大量的水印由于量化系数过大而丢失,因此在嵌入水印时,应适当的加强水印的嵌入强度,即加大量化因子d的值,以弥补这种损失。通过对图1进行分析,量化因子在5~20范围内时,各种嵌入方案图像的PSNR均大于40dB,因此选择量化因子范围为5~20。
2.2 确定量化因子取值
在2.1节实验的基础上,本节将通过考虑在取值范围内的各量化因子经过图像压缩后的表现来确定量化因子的具体值。变化d的值分别为5、6、10、15、20,对图像进行不同程度的JPEG压缩,Quality表示为图像品质因子,Quality值越大表明图像压缩率越低,经过压缩后的图像质量越高。通过实验可得到随着Quality的变化,PSNR和BER的变化曲线。取经过Zig-Zag扫描后的DCT系数的第4、5、6、7、8位嵌入水印,即range_dct=4:8(由于其他各种频段嵌入策略与此方法所得到结果基本类似,实验结果不失一般性)。实验结果表明,当d=5时,随着PSNR逐渐升高,BER逐渐降低,PSNR和BER两条曲线的拟合程度最好;而当d取其他值时,BER的数据容易出现反复,不能很好的体现PSNR和BER的关系,所以量化因子最优取值应为5。图2为d取值为5和6时的BER与PSNR随着质量因子的变化而变化的曲线图。
2.3 确定水印嵌入区域
在确定了量化因子d的取值的基础上,本节将通过实验确定采用哪些频段系数进行水印嵌入。
给定量化因子d=5,对图像采用有损JPEG压缩,得到各种嵌入策略的PSNR和BER随着图像质量因子变化而变化的曲线,通过比较这两种曲线的近似度,选择PSNR和BER曲线图拟合效果最佳的嵌入策略作为最终的嵌入策略。如2.1节所述,为了能够使提取的水印表征载体图像的质量,选择在中低频系数中嵌入水印,因此可选的嵌入策略包括在低频,中频,中低频这三个范围内进行嵌入。本实验选取四种情况进行实验,分别是:(a)在DCT系数的第2、3、4、5、6、7、8、9、10位嵌入水印,(b)在DCT系数的4、5、6、7、8位嵌入水印,(c)在DCT系数的第12、14、16、18、20、22、24、26、28位嵌入水印,(d)在DCT系数的第4、6、8、11、15、21、26、28、32位嵌入水印。分别对应图3中(a)-(d)图。
通过图3可以发现,当取第4个到第8个DCT系数时,BER与PSNR之间的拟和度最好,而在其他嵌入策略中,BER会有不同程度的反复。因此确定水印嵌入位置为原始DCT系数经过Zig-Zag扫描后的第4个到第8个系数。在8×8大小的块中的具体位置如图4中黑色块区域所示:

图4 水印嵌入系数示意图
综合2.2和2.3节中的分析,最终确定水印嵌入时量化因子(水印嵌入强度)为d=5、选择在DCT变换系数中的低频系数,即按照zigzag扫描顺序的第4个到第8个系数进行水印嵌入。
2.4 PSNR和BER相关性分析
在上一节中对文中所提出的算法的几个关键系数的选取进行了分析,从而获得了在保持水印不可见性下,能够更好的反映图像质量变化的水印嵌入算法。本节将分析PSNR与BER之间的关系,并给出两者具体的关系表达式,从而达到利用BER来估计图像PSNR的目的。
由图3(b),在d取5,DCT系数选择4~8区间系数情况下,所获得的PSNR与BER之间的关系图可以看出:当PSNR增大时,BER会随之减小,即PSNR和BER有很强的线性相关性。因此本算法将利用一阶多项式来拟合PSNR与BER之间的关系,即:

通过线形拟合,计算得到:a1和a2分别为55.1797和-25.7508。即:

2.5 实验结果验证
为证明算法可行性和验证实验结果准确性,选取幅面为768×512的标准测试图片Bird进行算法验证。在Bird图片中嵌入水印,然后对其进行JPEG压缩,获得在不同质量因子时,图像真实PSNR。从压缩后的水印图像中提取水印并得到提取水印的BER。利用式(4)求得预测PSNR′,并求得预测PSNR′与原始PSNR之间的差值。
图5中(a)为原始宿主图像,(b)为实验采用的幅面为72×44的二值水印图像,(c)为JPEG压缩因子(Quality)为60时,嵌入水印后的图像,(d)为对应的水印提取图像。对比(a)(c)两幅图像可以发现,水印不可见性非常好,在(c)图中看不出水印嵌入痕迹。

图5 提取水印实验结果图
计算Birds图片分别在不同压缩比情况下的PSNR和对应的BER,然后用公式(4)直接得到PSNR′值,比较PSNR和PSNR′误差δ,从而来判定水印算法的可行性。


表1 JPEG压缩下的PSNR与估计值PSNR′
实验数据如表1所示:将实验数据带入式(5)中求得误差均值:

由上述结果可以看出,图像经过JPEG压缩后,由BER得到的PSNR′可以较精确的估计图像PSNR的真实值。
3 结论
本文提出了一种提出了一种基于图像DCT域嵌入水印的方法。该算法考虑DCT域的心理视觉模型和图像压缩对提取水印质量的影响,将水印嵌入到分块DCT域的中低频段系数中,保证了水印的不可见性和鲁棒性。通过大量实验和数据,确定了水印嵌入的量化因子以及具体的中低频系数嵌入区域,并得到了图像峰值信噪比(PSNR)与水印的像素错误率(BER)之间的线性关系。利用该线形关系对经过JPEG压缩后的图像PSNR进行预测,结果表明本算法能够比较准确的对图像质量进行估计,平均估计误差小于4%,可用于实时图像压缩传输系统中的视频质量评估。
[1]王新岱,杨付正.视频质量的主客观评估方法研究[J].电视技术,2003,254(8):81-84.
[2]殷晓丽,方向忠,翟广涛.一种JPEG图片的无参考图像质量评价方法[J].计算机工程与应用,2006,18:79-81.
[3]Ingemar J.Cox,Matthew L.Miller,Jeffrey A.Bloom.数字水印[M].王颖,黄志蓓,译.北京:电子工业出版社,2003:17-241.
[4]曹华.图像和视频水印嵌入新方法研究[J].武汉:华中科技大学图书馆,2006.
[5]Campisi Patrizioi,Carli Marco,Giunta Gaetano,et al.Blind quality assessment system for multimedia communications using tracing watermarking [J].IEEE Transaction on Signal Processing,2003,51(4):996-1002.
[6]Sheikh HR,Wang Z,Cormack L,et al.Blind quality assessment for JPEG2000 compressed images.Conference Record of the Asilomar Conference on Signals[J].Systems a nd Computers,2002:1735-1739.

