压裂回接管柱的受力变形分析与计算

张 勇

（中国石油大学（北京）石油工程教育部重点实验室，北京 102249）

水力压裂技术作为最常用的一种油气井增产、注水井增注的重要技术措施，已在国内外得到广泛应用，并且经济效益显著。水力压裂过程中，压裂回接管柱将承受地面高压泵组施加的强大内压、高密度压裂液给予的静液柱压力、温度变化引起的轴向伸缩、管柱自身重力引起的压缩、井口钩载（悬挂或者挤压）、压裂液压入地层时引起的粘滞摩擦阻力和悬挂器或者水力锚的反作用力等[1]。井下管柱的内、外温度和压力变化，会引起压裂回接管柱伸缩、膨胀等变形，造成回接管柱脱出结合部位引起失封、对封隔器挤压引起封隔器失效以及引起油管自身破裂、套管损伤等；从而影响压裂施工或产生严重的后果。所以，压裂回接管柱的受力与变形分析，是保证管柱设计满足压裂工况、实现安全有效压裂的前提条件[2]，也是影响压裂施工成败的关键因素之一。

1 力学计算模型的建立及分析

由于压裂回接管柱上端坐挂在井口，下部由水力锚锁定在套管柱上。因此，将回接管柱简化为两端固定，中间管柱为均匀的弹性空心管，并且略去封隔器上端水力锚的影响、忽略油套环空压力的变化、粘滞摩阻力以及回接插头与回接筒的阻力。设压裂管柱的总长度为L（井口到回接筒），油管柱的内外径分别为d 和D，油管柱线重为q，管柱内流体密度为ρi，管柱外的流体密度为ρo，Po为管柱外壁环空压力，Pi为管柱内壁受到压裂液和泵压施加压力，Ao、Ai各为油管内外径截面积，Ap为密封管的截面积；回接管柱模型（见图1）。压裂过程中存在多种效应并存，影响井下压裂油管柱受力变形，本文重点分析简化后的回接压裂管柱在管柱自重、活塞效应、鼓胀效应以及温度效应影响下的轴向受力与变形。

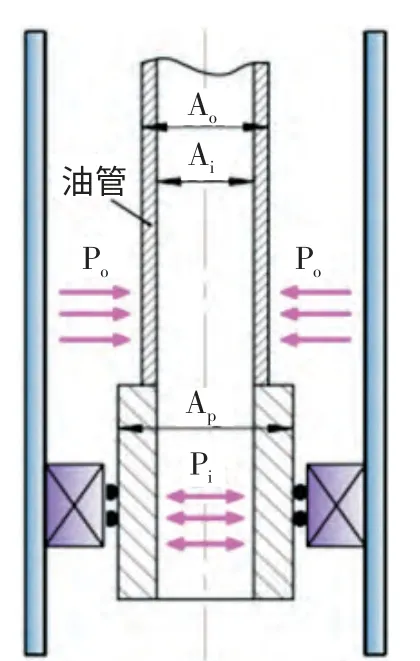
图1 回接管柱模型示意图

1.1 自重效应分析

管柱在深度h 处微元dh 的重力分析，该微元上部受到上部管柱重力引起的压力qh 的作用，下部受到支撑反力q（h+dh）的作用。距井口为h 的截面处压裂油管的轴向载荷Fg为：

重力引起的轴向总变形长度Hg为：

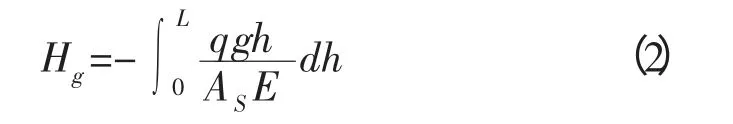
而初始管柱坐挂力PC作用于整个管柱，在任何截面上的应力均为PC，由胡克定律可知，坐挂力引起的轴向总变形长度HC为：

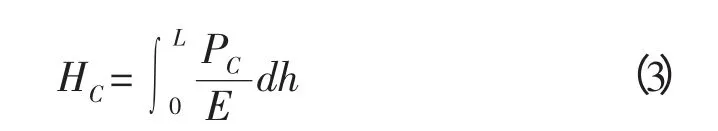
其中，PC=Fg/As，所以由自重所引起的轴向变形为：

1.2 活塞效应分析[3]

由回接管柱内外压力引起的对管柱的作用力称为活塞力，相应由油管柱内外压力的变化引起油管的伸长或缩短的这种现象称为活塞效应。分析管柱的轴向受力为：

向上的作用力：F1＝Pi（AP－Ai）

向下的作用力：F2＝P0（AP－A0）

取作用力向上（压缩力）为正，作用力向下（伸长力）为负。

则活塞力为：

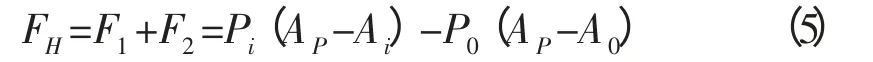
如果管柱内、外压发生变化时，将引起活塞力的变化。而活塞力的变化为：

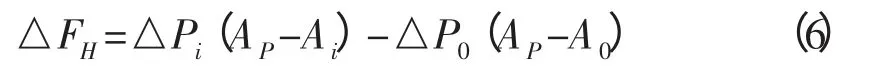
依据胡克定律（假设管柱缩短为负，伸长为正）得出管柱的变形公式为：

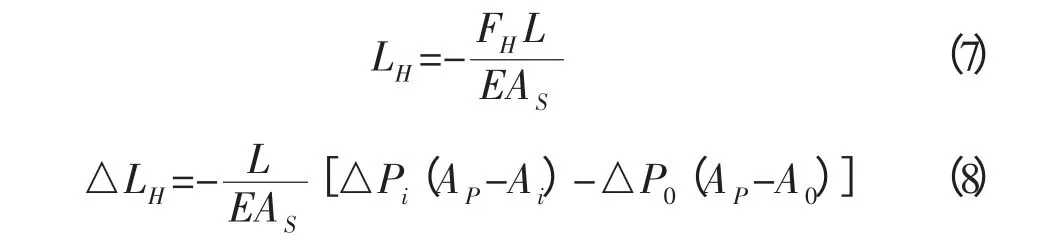
式中：L－管柱的长度，m；E－弹性模量，Pa；AS－管柱截面积，m2。

1.3 膨胀效应分析

管柱内、外流体压力的变化，使管柱发生膨胀的现象，称为膨胀效应（见图2）。由于膨胀效应发生在整个管柱上，因此在计算膨胀效应时，主要考虑管柱内、外平均压力的变化；同时，忽略流体密度的变化、流动引起的压力降及认为环空压力不变[3-4]。回接管柱任意截面处管内和管外分别受到P0和Pi的力。由弹性力学原理可知，管柱沿程受内压外挤所引起的管柱轴向变形长度和膨胀力分别为：

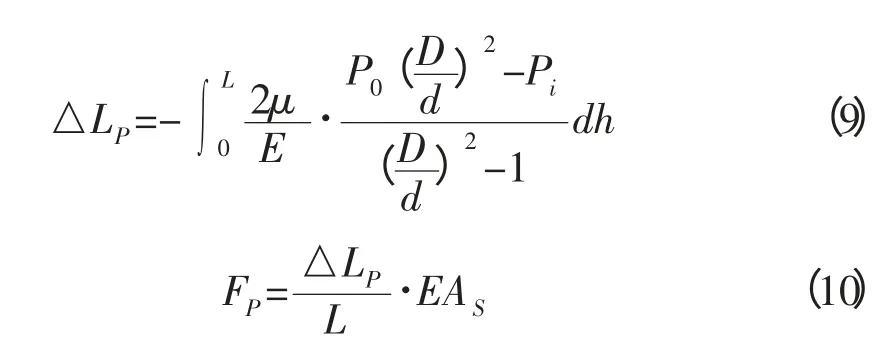
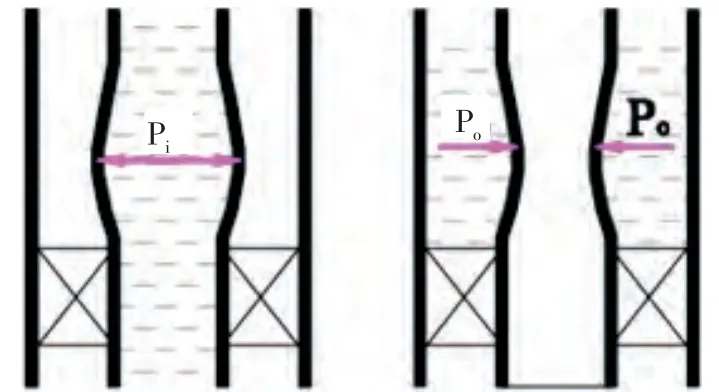
图2 膨胀效应示意图

1.4 温度效应分析[1,4]

压裂作业中，井内液体温度由于井深发生变化，管柱温度也随之变化，管柱受冷会缩短，受热会伸长，这就是管柱的温度效应。温度变化引起的管柱轴向应变ε 为：

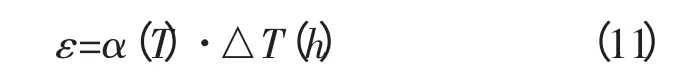
式中：α（T）-管柱线膨胀率，℃-1；△T（h）-管柱温度变化值，℃。

温度引起的总变形长度为：

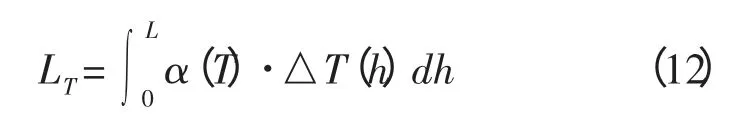
井口位置温降为△T1，底部H水力锚处温降为△T2可以计算出：

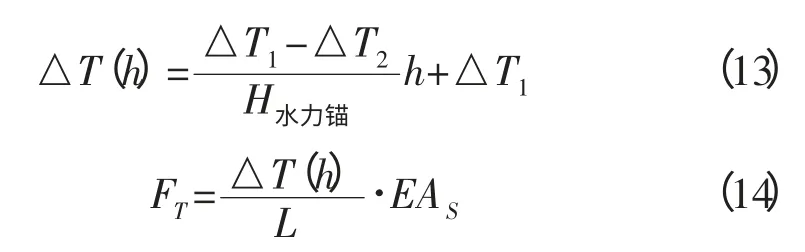
2 算例分析

假设回接管柱坐挂在井口且完全插入回接筒中，忽略回接筒长度和屈曲效应。参数：油管内径d=100.6 mm，外径D=114.3 mm，回插管内径di=100.6 mm，外径Di=120.5 mm，线质量q=29 kg/m。油管长度L=5000m，环空流体密度ρ=1.2 g/cm3，压裂时油管内流体密度ρ=1.4 g/cm3，压裂时井口温度下降10 ℃，回接筒处温度下降60 ℃。计算分析泵压分别为40、60、80、100 MPa时，压裂回接管柱的轴向力及轴向变形。

2.1 自重效应计算分析

根据1.1 的分析，并由公式（2）（3）（4）分别计算重力和坐挂里引起的管柱轴向变形量Hg、HC，进而求取管柱自重引起的轴向变形ΔHG。计算出自重所引起的轴向变形随管柱长度L 变化的趋势（见图3）。从图3可以看出，当管柱长度（井深）小于一定值时，自重引起的轴向变形的整体趋势为随管柱长度L 的增大而增大。当管柱长度L 超过一定值（图上显示约4 000 m）时，轴向变形的整体趋势为管柱长度的增大而减小。

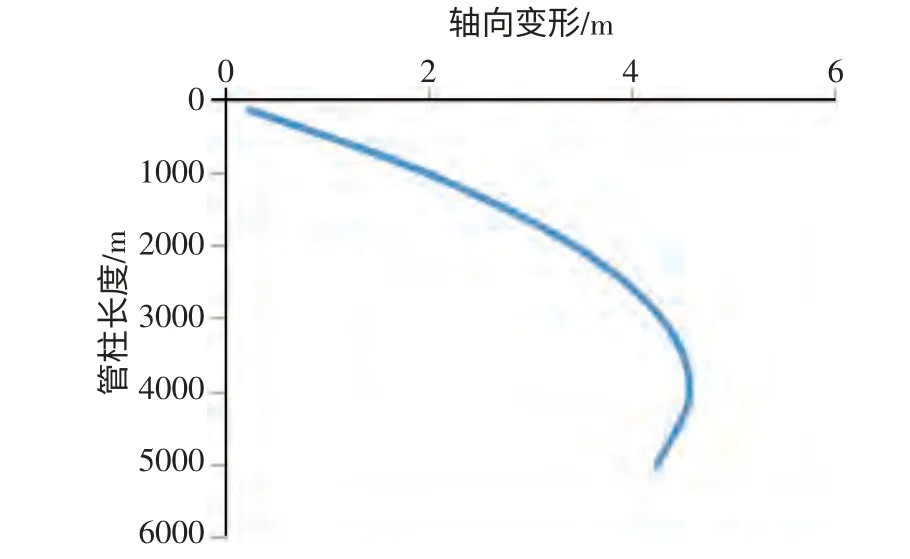
图3 自重引起轴向变形量随管柱长度的变化关系图

2.2 活塞效应计算分析

根据1.2 所述分析，计算得到不同泵压下活塞效应引起的活塞力随管柱长度L 的变化关系（见图4）。由图4 可以看出，管柱相同的情况下，泵压越大，则活塞效应引起的活塞力越大，轴向变形量大；且在相同泵压时，活塞力与轴向变形量都随管柱长度的增大而增大。

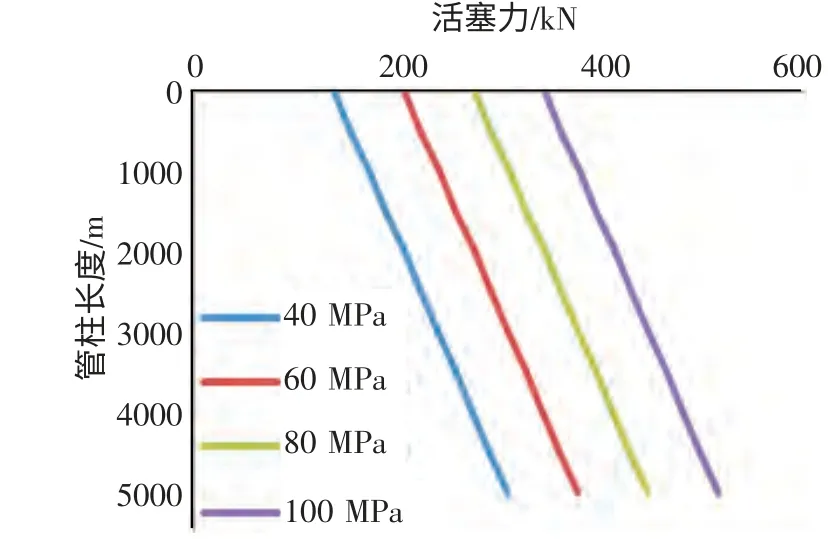
图4 不同泵压下活塞力随管柱长度的变化关系图

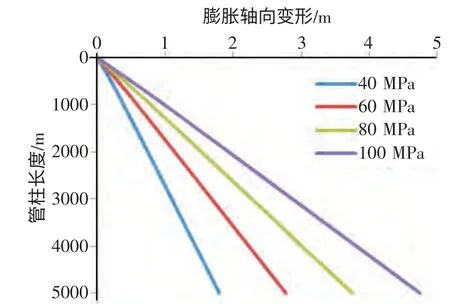
图5 不同泵压下轴向变形随管柱长度的变化图

2.3 膨胀效应计算分析

由1.3 所述计算不同泵压情况下，膨胀力随管柱长度L 的变化以及膨胀效应引起的轴向变形随管柱长度L 的变化可知：泵压越大，则膨胀效应引起的膨胀轴向力越大，膨胀轴向变形量大；且在相同泵压时，膨胀轴向力与膨胀轴向变形量都随管柱长度的增大而增大。而膨胀力随管柱长度的变化较小，轴向变形随管柱长度的变化（见图5）。

2.4 温度效应计算分析

计算温度效应引起的轴向力及轴向变形随管柱长度的变化得出：温度效应引起的轴向力和轴向变形均随管柱长度L 的增大而增大；且轴向变形量随管柱长度L 的增大，变形越严重（见图6）。

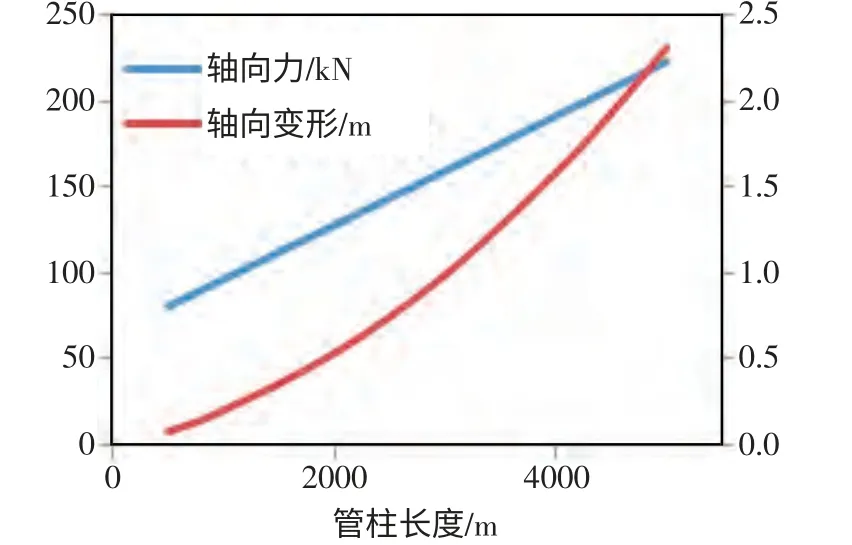
图6 温度效应下轴向力及轴向变形的变化图

2.5 管柱轴向力计算分析

压裂时，管柱同时受到自身重力、活塞力、水力锚支撑力、膨胀效应以及温度效应引起的轴向力变化和管柱轴向变形。计算压裂状态不同泵压情况下，轴向力的大小随管柱长度L 的变化趋势（见图7）。

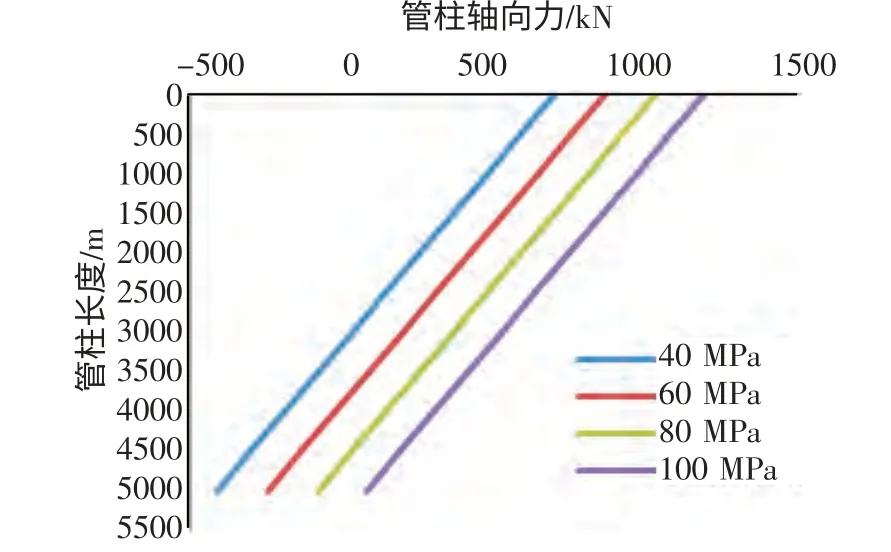
图7 不同泵压下管柱轴向力的变化趋势图

2.6 管柱轴向变形计算分析

据本不同效应对管柱所产生的轴向变形情况，并令管柱沿轴向受拉伸为正受压缩为负。轴向变形：△L=ΔHG+ΔLP＋LT＋ΔLH。计算不同泵压下管柱的轴向变形情况（见表1）。并分析可知管柱的轴向变形随着泵压的增大，形变量由拉伸向压缩过度并且随压力的增加压缩形变量越来越大。

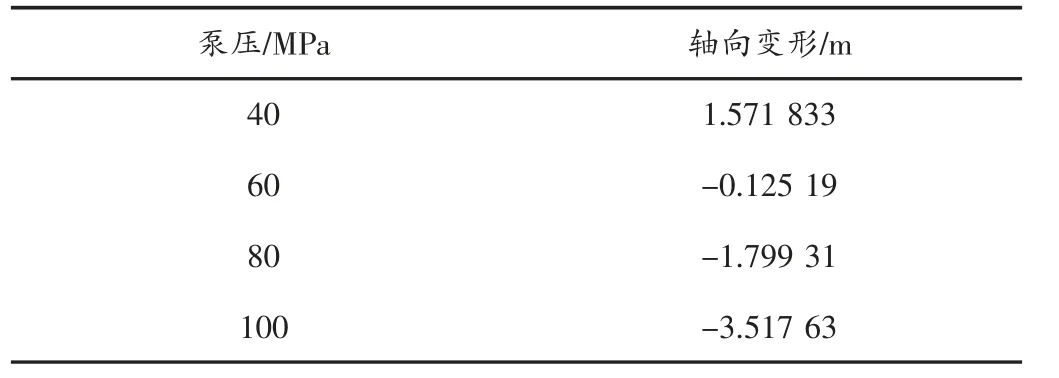
表1 不同泵压下管柱的轴向变形量

3 结论

（1）建立了压裂回接管柱的力学计算模型，结合实际算例分析管柱在自重、活塞效应、鼓胀效应以及温度效应影响下的轴向受力与变形规律。

（2）泵压越大，管柱受活塞力越大，轴向变形量大；膨胀效应引起的膨胀轴向力越大。且在相同泵压下，轴向变形量均随管柱的伸长而增大；温度效应引起的轴向力和轴向变形均随管柱长度L 的增大而增大。

（3）当泵压恒定时，管柱所受轴向力随管柱长度的增大而减小，管柱的轴向变形随着泵压的增大，形变量由拉伸向压缩过度并且随压力的增加，压缩形变量越来越大。因此，在压裂施工前，应该保证管柱设计满足压裂工况的要求。

［1］ 荣准，尹浚羽.水力压裂回接管柱受力分析［J］.重庆科技学院学报（自然科学版），2013，15（S1）：72-76.

［2］ 刘巨保，岳欠杯.石油钻采管柱力学［M］.北京：石油工业出版社，2011：188-190.

［3］ 杨魁.同井注采封隔器设计及管柱力学分析［D］.青岛：中国石油大学（华东），2011.

［4］ 生丽敏.井下管柱力学分析及优化设计［D］.成都：西南石油学院，2005.

［5］ 崔玉海，唐高峰，丁晓芳，等.注水管柱中温度效应的分析与计算［J］.石油钻采工艺，2003，25（2）：50-54.