高频窄脉冲电流电解加工叶片过程的耦合场数值模拟

秦艳芳， 张晔， 江伟

（合肥工业大学机械与汽车工程学院，合肥230009）

0 引言

以周期间歇性供电代替直流加工模式下的连续供电，使工件发生周期断续的溶解是脉冲电流电解加工的基本原理［1］。当电解加工采用高频窄脉冲电源时，阳极工件发生频率较高的断续的溶解反应，加工间隙中的物理化学特性、电场中的电流密度和流场在脉宽间隔区域的恢复改良了电流效率的曲线特性，加工间隙缩小，阳极的集中蚀除能力增强，因此加工精度、表面质量和加工效率得以提升［2］。对高频微秒级脉冲电解加工进行原理探究，对优化加工过程中的工艺参数及其在精密加工中的应用具有非常重要的意义。

电解加工的数值模拟一直是国内外研究的热点问题［3-4］。早期的仿真研究模拟的基本是电场和流场两个独立的场，而实际上电解加工呈现出典型的多物理场耦合作用，在这种情况下如果仅仅进行单物理场的分析计算（或称为计算仿真），不能反映实际加工过程中电场与流场之间的相互作用，显然得不到与现实情况相近或完全相符的仿真结果。

1 理论背景

电解加工是一项复杂的电化学加工过程，其中涉及到电场、流场、温度场、化学反应以及结构场之间的交互作用，为了能够清晰地看出耦合关系，用有向图表达，如图1所示，场与场之间的耦合作用用有向线段来表示，箭头从源场指向作用场。

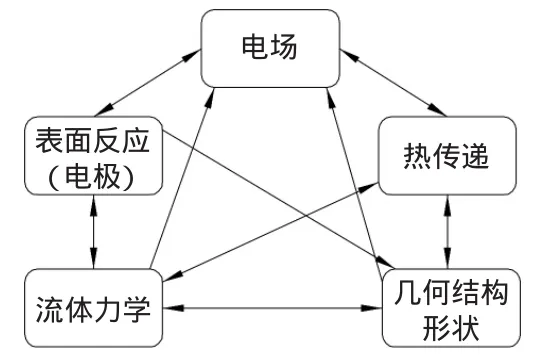
图1 电解加工多场耦合关系图

1.1 电解加工间隙中的电场特性

假设电解液满足各向同性，则电场的电位分布应符合拉普拉斯方程；在电解加工过程中，阳极溶解质量和通过电解池的电量符合法拉第定律。根据欧姆定律，可用如下的数学方程组来表示电解加工间隙中的电位分布：

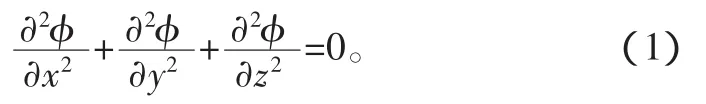
阳极表面的边界条件

阴极表面的边界条件：

式（1）～式（3）中：φ 为电场中各点电位，通常 φ=φ（x，y，z）；U为阳极表面电位值；n为阳极表面各处的法向坐标；θ为阴极进给速度与阳极被加工表面法向间的夹角；η为电流效率；η0表示θ=0°处的电流效率；i为电流密度，一般认为，沿极间间隙中阳极表面的同一法线上各点的i值相同，可写作i=i（θ）；i0表示θ=0°处阳极表面法向上的电流密度；κ为电解液的电导率。

1.2 电解加工过程中的间隙流场分析

在电解加工过程中，阴极析出氢气，阳极溶解产生电解产物。故在加工间隙中应是气、液、固三相流，由于电解产物所占的体积比很小，对电解液电导率和密度的影响亦很小，因此常将加工间隙中流场近似看作是气液两相流。

为使研究问题得到简化并不失其本质，可做出如下假设：

1）两相均匀流型假设。气泡在电解液中均匀分布，电解液不能压缩，气相状态变化服从理想气体状态方程；相间无质量变换，沿流动方向的每一横截面上各相参数分布均匀［5］。

2）热平衡状态假设。由于电解液流程较小，忽略电解液的温度变化和温差造成的能量耗散，假设电解液与两极间的热交换处于热平衡状态，电解液温度保持恒定。

根据质量守恒定律、动量定理和能量方程，可得电解加工间隙模型的基本方程组为

以上方程组中：Δ为电解加工间隙；β为气泡率；u为电解液流速；p为电解加工间隙中的压力；Rg为氢气的气体状态常数；T为电解液温度；ηg为析氢的电流效率；kg为析氢质量电化当量；x为电解液的流程；ρ1为电解液密度；τ为黏性剪切力；UR为加工间隙方向上电解液的欧姆压降；n为考虑气泡率β对电导率影响的指数，一般从1.5～2中选取，通常可取1.5。参数下标“0”为间隙进口处参数，未加下标为流程x横截面上的参数。

1.3 电解加工中流场、电场的耦合关系分析

流场诸多参数中对电解加工的成形规律起主要影响的是电导率，而电解加工过程中电导率的变化主要受气泡率和电解液温度的影响。气泡是在电场存在的前提下发生电极化学反应生成的。本文研究的脉冲电解加工耦合关系是流场与电场之间的，电导率作为耦合变量。为简化问题，忽略温度对电导率的影响，设定电解液温度为25℃，则

1.4 氢气浓度与电导率的关系公式推导

由式（5）可知，氢气成分的增加会使电导率变小。通过电场模拟分析可得到氢气的浓度，需要用数值求解的方法计算一定物质的量浓度时氢气的体积分数。假设加工过程中加工间隙的压强大小为P，则根据理想气体状态方程

式中：V为气体的体积，n为气体物质的量，T为一定环境下的温度，R为气体常数。

其中，R≈8.31 J/（mol·K），T=298.15 K，κ0=14.7 S/m。

2 建模和仿真

2.1 耦合场仿真策略分析

本文选用COMSOL Multiphysics进行电解加工叶片的耦合场仿真。由于所分析的内容涉及电解加工的电场、流场、化学反应和化学反应生成物的传递，应选择流体模块、电化学模块和化学物质传递模块［6］。

电解加工是一个阳极不断溶解、阴极不断析出氢气的瞬时过程，本文分析的电解加工是在高频微秒级脉冲电压的情况下进行的，故应选择瞬态求解。由于电解液在进入加工间隙时有一定的入口压力，给了流场一个一定的初始速度场和压力场，为求得这个初始速度场和压力场，要先进行流场的稳态求解。

2.2 叶片分析模型的建立

图2 电解加工叶片示意图

叶片采用侧流式叶片双面加工，同时附加背压，图2为电解加工叶片的二维示意图，具有一定压力的电解液从左侧进液口进入加工间隙，整个加工间隙充满高速流动的电解液。工具阴极外形轮廓、阴极进出液口、工件加工型面和加工间隙构成电解加工中间隙流场区域。

为简化问题，本文中采用AutoCAD建立了加工间隙区域的二维几何模型，工件和阴极分别以工件轮廓和阴极外形轮廓表示。所建流场二维模型如图3所示。

图3 电解加工间隙区域的二维模型

叶片模型导入后进行适当的几何模型修复处理并划分网格，如图4所示。

图4 模型局部网格

采用10 kHz脉冲电源频率（其方波峰值电压为15 V，占空比为0.5）进行电解加工过程模拟。

3 模拟仿真结果对比与分析

为了对比直流电解加工与高频微秒级脉冲电解加工两种情况下加工过程的不同，本文首先进行了直流电解加工叶片的仿真分析。其他加工参数不变，电压设为恒定15V。

图5 直流电解加工间隙的电势场

图6 t=0.005 s时的电流场

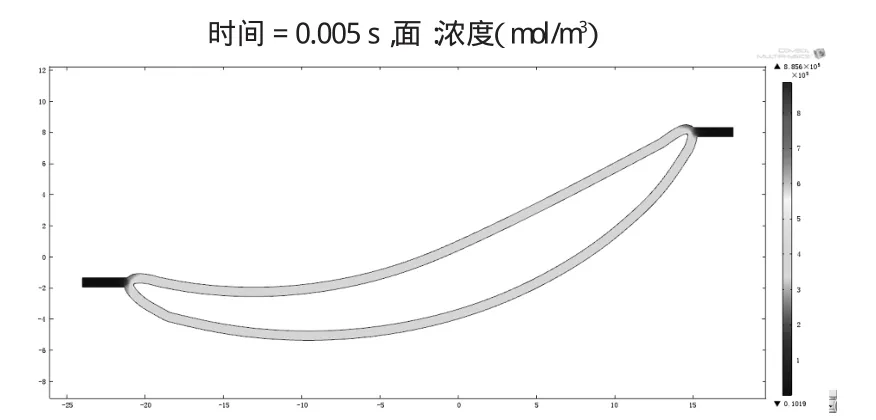
图7 t=0.005 s时的氢气浓度

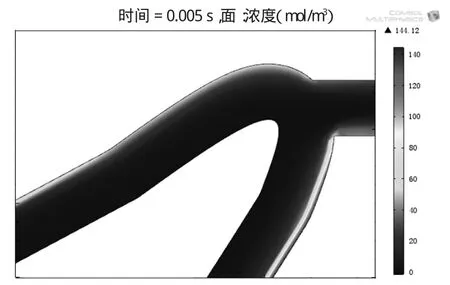
图8 t=0.005 s时局部加工间隙的氢气浓度

按式（9）计算出相应的气泡率和电导率，并继续进行下去，最终得到t=0.01 s时电解液的电导率。以同样的方法得到脉冲电解加工叶片t=0.01 s时电解液的电导率。对数据进行相应的整理后，分别得到如图9、图10所示的脉冲电解加工和直流电解加工的氢气浓度、气泡率、电导率的变化趋势图。

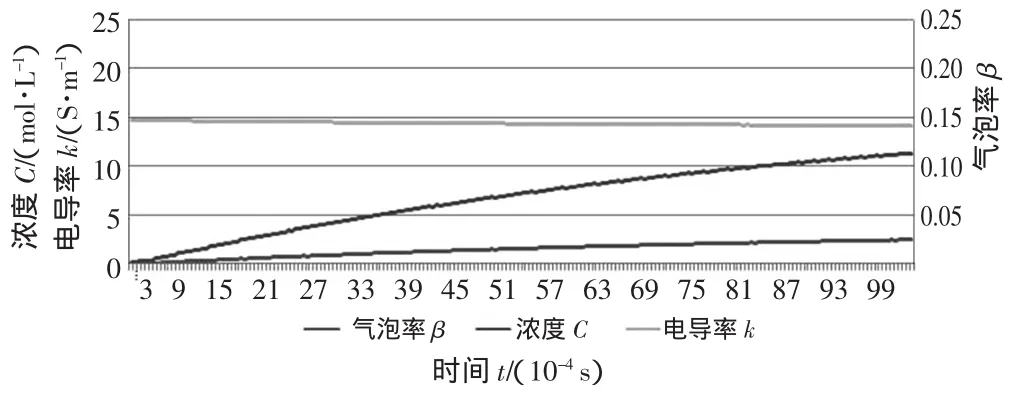
图9 脉冲电解加工的氢气浓度、气泡率、电导率变化趋势图

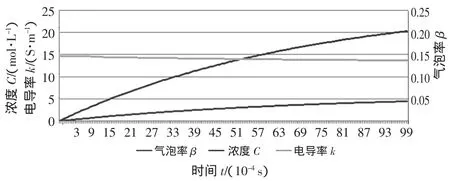
图10 直流电解加工的氢气浓度、气泡率和电导率变化趋势图

通过对比图9和图10，可以看出在脉冲电解加工中每个周期的后半个周期，加工间隙中的气泡率增加幅度比前半个周期小；相应地，电导率的降幅也较前半个周期小，这是脉冲电流的脉冲效应所引起的。在脉间时间段内，加工间隙的流场得以恢复，部分气泡被电解液从加工间隙的出液口带离。而在直流电解加工中，阴阳极电势差恒定，阴极不断析出氢气，故在所研究的时间段内，氢气浓度持续上升，电导率持续减小。在表面质量方面，一般情况下是表面质量随i的增大而改善。在加工精度方面，电流密度i的影响是：一定的加工电压和电导率条件下，i越高，加工间隙Δ越小，越有利于提高加工精度。电导率不仅影响电流密度参数，还与电解加工的平衡间隙息息相关，而平衡间隙也会对加工精度造成影响。

4 结语

本文综合考虑流场和电场之间的耦合作用，推导出与生成氢气浓度有关的电导率公式。通过建立电解加工叶片加工间隙区域的二维几何模型，进行了高频窄脉冲电解加工和直流电解加工叶片的多场耦合数值模拟，对比结果表明，脉冲电解加工能够有效削弱由于流场中气泡率的影响造成的电导率变小，有利于维持稳定的电解液电导率和较高的电流密度，从而得到更高的表面质量和加工精度。

［1］ 徐家文，云乃彰，王建业．电化学加工技术——原理、工艺及应用［M］．北京：国防工业出版社，2008．

［2］ 范植坚，王天诚．电解加工技术及其研究方法［M］．北京：国防工业出版社，2004．

［3］ Kozak J.Computer Simulation System for Electrochemieal Shaping［J］.Journal of Materials Proeessing Technology，2001，109（3）：354-359.

［4］ 钱密，徐家文．数控展成电解加工的阴极结构及流场研究［J］.航空精密制造技术，2003，39（2）：14-18．

［5］ 王建业，徐家文．电解加工原理及应用［M］．北京：国防工业出版社，2001.

［6］ 中仿科技公司.COMSOL Multiphysics有限元法多物理场建模与分析［M］.北京：人民交通出版社，2007.