一种系统级多维振动试验技术

王晓飞，王 刚，高贵福，李军利

（北京机电工程研究所，北京 100074）

0 引言

振动试验是航空航天产品环境适应性考核和可靠性增长的一种有效手段[1]。目前，系统级振动试验一般在单轴振动试验系统上进行，可以使用一个或者多个振动台，但激励的方向都在一个轴向上。而实际上，航空航天产品在使用和运输过程中所处的振动环境都是多轴向且相互耦合的。某些航天产品特别是对方向敏感的元件在单轴振动试验与真实振动环境中的响应输出会有一定的差距。例如：某航空研究所对某精密设备故障归零时，采用单轴振动台施加50g大量级激励，并没有实现故障的复现，而转到3 台振动台进行三轴向试验，加载 到5g即复现了该故障。这说明，多台多轴振动试验确实可以提高故障激发效率，弥补单轴振动在环境模拟中的一些不足[2]。

目前，国内在多维振动试验技术方面，针对小尺寸、设备级的研究和应用较多，而对大尺寸、系统级的研究较少。本文针对航空航天领域中的细长体、大尺寸、系统级产品开展了多维振动试验技术研究，分别在水平和垂直方向各使用2 个振动台。通过运用多维解耦、多维控制等技术，可以实现在同一方向不同位置及同一位置的不同方向上施加各自不同量级的振动激励，更加真实地模拟振动环境，更有效地暴露产品的潜在缺陷。

1 多维振动试验原理

多维振动试验采用的振动台数应与所要控制的响应点数相匹配。控制谱矩阵的维数等于系统自由度数，其对角项为该自由度的自谱密度，非对角项为自由度间的互谱密度。4 台振动试验对应每一个频率，其控制谱矩阵包括16 个元素：

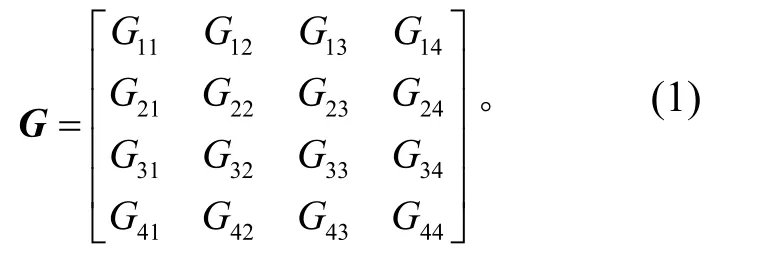
互谱密度用极坐标表示时，则有

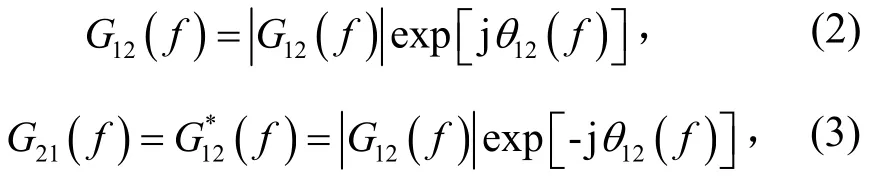
得到

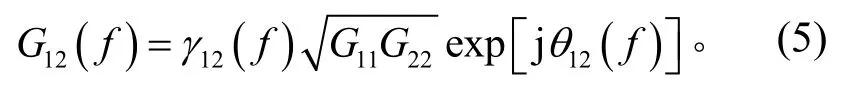
自谱密度是实数，可用预示或遥测和包络的方法得到[3]，本系统中自谱的设定与单轴振动相同；互谱密度是个复数，难以用例行的方法得到，是目前多维振动应用的难点[4]，对于互谱的设置，本系统将人为给定相干系数和相位角数值，并设置适当的容差，以达到原理性验证的目的。

2 多维振动试验系统设计方案

多维振动试验系统主要包括振动台、机械解耦装置、振动控制子系统、工装夹具和模拟试验件，采用无公共台面且局部分别激励的布局（如图1所示）。在该布局中，每个振动台通过机械解耦装置、工装夹具与试验件相连，激励点选择在试验件上刚度较大的部位。与带有公共台面的布局形式相比，局部分别激励的方法避免了公共台面对振动传递的影响。由于振动台可以从不同的位置直接激励试验件，所以在同一方向的不同位置能够实现量级不同的试验条件。因此，局部分别激励的布局比较适合较大外形尺寸的细长体结构且对试验条件要求 较复杂的系统级产品[5]。

系统设备的指标见表1。

图1 多维振动试验系统的局部分别激励式布局 Fig.1 Layout of local respective excitation of multi- dimensional vibration test system

表1 多维振动试验系统中各设备指标 Table1 Specifications of the multi-dimensional vibration test system

3 关键技术

3.1 多维振动解耦

机械解耦是多维振动试验系统的一个重要环节，其解耦装置既要保证在传力方向上具有足够的刚度，使振动台动圈与试验件保持无相对运动，又要在非传力方向上不对运动自由度产生限位约束，以免对振动控制和响应品质造成不利影响。

本研究设计的多维振动试验系统对解耦装置提出了较高的要求。首先在20～2000 Hz 的振动频率范围，对解耦装置的高频传递特性要求很高。其次，由于细长体结构的试验件前后具有2 个激励位置，每个激励位置又同时有垂直和水平2 个激励方向。对于相同方向的不同激励位置，若运动不同步，势必产生试验件的转动；对于同一激励位置的不同方向，试验件又要在1 个平面内的2 个方向上实现自由平动，这就要求系统的解耦装置在一定范围内既能实现转动解耦，又能实现平动解耦。

目前在工程中使用较多的机械解耦装置主要有两类：自润滑滑动机构和静压油膜支承滑动机构。

自润滑滑动机构中常见的形式为十字滑轨式，通常由2 个重叠的、运动方向相互垂直的直线滑轨组成，滑轨的轨道用机械结构连接，滑轨间采用润滑油润滑或自润滑。垂直于滑轨的运动方向为传力方向；由于在传力方向上存在滑轨间隙，因此高频传递特性往往不好。

静压油膜支承滑动机构是利用油腔内的高压油膜使运动的轴承始终处于动态平衡的中心位置。油膜的不可压缩性实现了在传力方向上的动态刚度，油膜的流动性则在非传力方向上产生了润滑效果，实现了运动的解耦。目前应用于振动试验的有两种类型：平面静压式和静压球头式。平面静压式与十字滑轨式类似，由高压油膜代替了自润滑机构，在传力方向上由于存在油膜间隙，高频传递特性也不理想。此外，十字滑轨式和平面静压式都是“平面运动副”，只能实现平动解耦，无法实现转动解耦。

本文重点研究的是静压球头式解耦装置，如 图2所示，该装置具有上下半球形的铰链，内球面和外球面之间微米级的缝隙靠高精度的机械加工保证，缝隙间充入压力约20 MPa 的高压油膜，起到润滑和刚度保持的作用；内球面和外球面在一定角度范围（±6°）内可自由转动，实现对转动自由度的解耦。由于主轴的存在，与十字滑轨式和平面静压式相比，静压球头式的高频传递特性要好很多，一阶频率可达1200 Hz 以上。

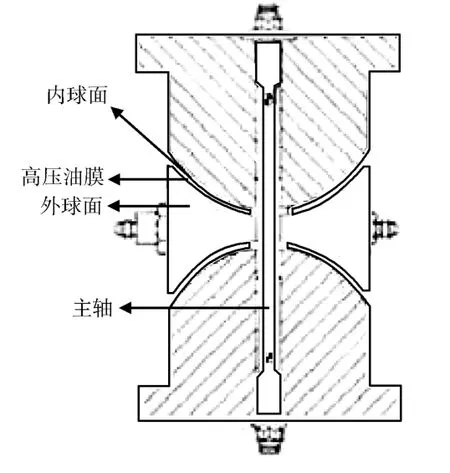
图2 双铰链静压球头式解耦装置 Fig.2 Double pivot hydrostatic spherical couplings

本研究巧妙地利用了一种双铰链的静压球头式解耦装置，当单个铰链转动时，可实现相同方向不同激励位置的转动解耦；当上下铰链配合转动时，又可将转动转化为一定范围内的平动，实现同一激励位置不同方向的平动解耦，满足系统的设计要求。双铰链静压球头式解耦装置的解耦效果如 图3所示。

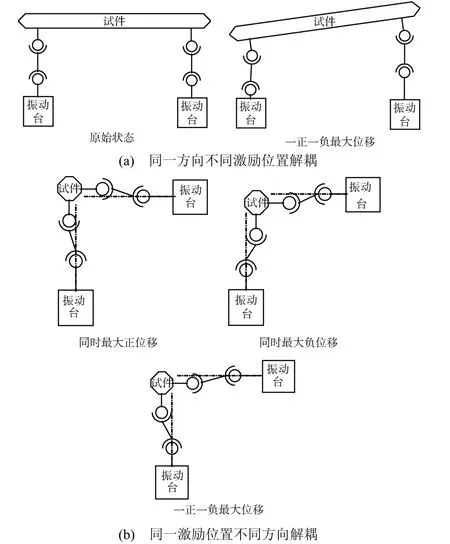
图3 双铰链静压球头式解耦效果示意图 Fig.3 Sketch of hydrostatic spherical decoupling

3.2 多维振动控制

多维振动控制是实现多维振动试验的关键技术之一[6-15]。在本研究中，自行开发了一套基于“矩阵幂次法”多维振动控制软件，并通过验证试验将其与商业软件进行了对比，结果表明该控制软件能比较稳定、高效地实现自谱和互谱的控制。该软件的控制算法如图4所示，主要分为以下几步：

1）试验前用低量级独立白噪声激励试件，采用频响矩阵H1输出估算模型得到试件的频响函数，并计算得到补偿矩阵A，对参考谱R进行 Cholesky 分解，即R=L(0)L(0)H，得到初始的L(0)，为后面生成驱动谱作准备。

2）补充随机相位后，由式D=AL(0)X得到驱动信号的频谱，式中D为驱动信号；X为对角阵， 即其中θi是服从-π～π 均匀 分布的随机相位，经逆傅氏变换得到伪随机信号d。

3）对伪随机信号进行时域随机化，生成真随 机信号。

4）用真随机信号激励试件，并采集响应信号y。

5）计算出响应信号的功率谱Syy，并与参考谱R相比较，采用矩阵幂次修正算法 计算得到新的L(k)，其中上标k表示迭代次数；E是小量误差项矩阵；L是下三角阵，其初始值可用第(1)步中的L(0)；Ls为Syy的下三角分解，即Syy=Ls·LsH；

6）利用新的L(k)，重复第（2）步更新驱动谱，如此反复。

图4 多维振动控制算法框图 Fig.4 Flow diagram of multi-dimensional vibration control algorithm

在硬件方面，采用Agilent E8491B 模块实现工控机到VXI 系统IEEE1394 的通信和数据传输；采用Agilent E1432A 模块实现DSP、传感器信号调理、抗混叠保护、数字转换以及高速测量计算等功能；采用Agilent E1434A 模块作为信号源，集成了E1432A 和 E1433B 数字转换器，提供各种类型波形输出。硬件工作流程如下：由工控机上的软件计算得到的驱动信号经过E1434A 发送给功率放大器，使振动台按给定的信号工作；由粘贴在试件上的振动传感器测得响应信号，经E1432A 采集到VXI 中，再由工控机上的软件读取这些数据并作数据处理。

3.3 多维夹具设计

多维振动试验系统对夹具设计提出了较高的要求。在满足比刚度大、一阶频率高及密度分布均匀等常规要求的基础上，要求夹具能同时传递两个方向的振动，能与两个方向的解耦装置紧密连接，并且还要兼顾安装上的可调节性和可操作性。本系统对卡环型夹具进行了改进，设计了半圆形的转接块。转接块为上下一对，一端设计成为与夹具贴合的弧面，可以分别与上卡环和下卡环连接；另一端上下半圆可拼成圆形的连接面，实现与水平向解耦装置的连接。这样，改进后的夹具既能保持足够的刚度，又能同时与两个方向的解耦装置相连。由于水平向的解耦装置的自重会引起该方向振动台动圈的偏心，所以设计了弹性悬吊系统以抵消其自重。水平向连接效果见图5。

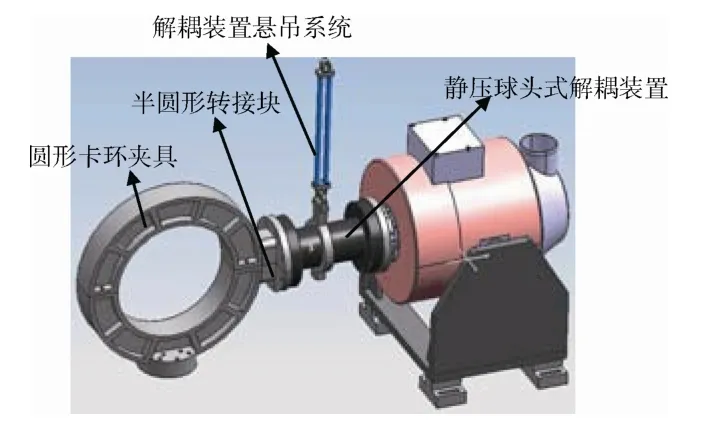
图5 夹具的水平向连接示意图 Fig.5 Sketch of horizontal connection

4 系统的安装

多维振动试验系统对系统安装精度提出了更高的要求。在水平向和垂直向振动台的推力方向上，以及在细长体试验件长度方向上，都需要准确地安装定位，每个方向装配尺寸链环数多，3 个方向的尺寸链相互制约，给安装工作带来了很大困难。系统安装时首先通过计算机辅助设计对系统的每个组件进行三维建模，然后进行虚拟装配；根据虚拟装配的结果，再对系统的安装布局进行优化设计。利用垂直向振动台的移动机构，实现其在试验件长度方向上定位；以垂直向振动台的高度为基准，设计水平向振动台支座的高度；设计带有可调节的安装孔的转接块，用于水平向振动台和支座的连接，可以实现水平推力方向和试验件长度方向上位置调节；利用6 个吊点的高精度步进式吊车，分别对试验件、解耦装置和水平向振动台进行吊装，完成系统的安装。系统的最终安装效果见图6。

图6 四台两轴振动系统最终安装的实物图 Fig.6 The four-shakers-two-axes vibration system connection

5 试验调试

分别采用自研软件和商业软件对四台两轴振动系统进行了调试，调试的振动频率范围为20～2000 Hz。由于调试采用的垂直向振动台比水平向振动台推力大很多，垂直向振动台的推力横向分量对水平向振动台会产生较大影响。因此，根据水平向振动台的能力，选择较小的调试量级，调试的垂直向总方均根值为0.5g，水平向总方均根值为0.3g，各激励点相对相位设为180°。

自研软件和商业软件的控制曲线如图7和图8所示。整个试验频率范围内，两种软件所控制的频谱基本都在±3 dB 允差线以内，超过允差的累积带宽不超过整个频带的5%，满足国家军用标准的要求，说明多维控制方式能够达到较好的控制效果。各激励点的相对相位控制曲线如图9所示，可看出在大部分频段内控制效果较好，说明多维解耦方式能满足多维振动试验的需要。值得注意的是，水平向振动台底座的刚度会对试验的控制效果产生影响，尤其在低频段影响较大，因此，在试验室条件允许的情况下，水平向振动台应采用刚度尽可能大的底座。

图7 自研软件试验控制曲线图 Fig.7 Control curve of verification test by self-developed software

图8 商业软件试验控制曲线 Fig.8 Control curve of verification test by commercial software

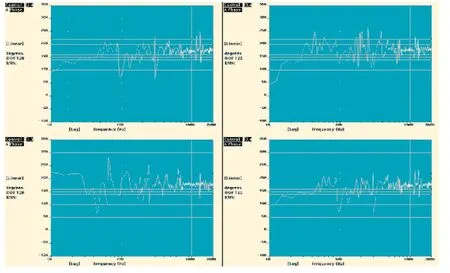
图9 各激励点相对相位控制曲线 Fig.9 Control curve of relative phase of the excitation points

6 结束语

新型飞行器的研制对高水平的振动试验技术提出了迫切的要求。国内外大量研究表明，多维振动是未来振动试验技术发展的一个重要方向，是对传统一维振动试验技术的有效补充。本文提出的多维振动试验技术初步解决了多维振动解耦、多维振动控制和多维夹具设计等方面的问题，为该项技术更广泛的应用提供了必要的技术支撑和经验储备。

（References）

[1] Keller T,Underwood M A.An application of MIMO techniques to satellites testing[C]//Environmental sciences and technology (ESTECH 2000).Newport,Rhode Island,2000-03-03

[2] 赵保平,王刚,高贵福.多输入多输出振动试验应用综述[J].装备环境工程,2006,3(3): 25-32 Zhao Baoping,Wang Gang,Gao Guifu.Application of multiple input and output vibration test system[J].Equipment Environmental Engineering,2006,3(3): 25-32

[3] Underwood M A,Russell A,Keller T.Filling in the MIMO matrix: using measured data to run a multi-axis vibration test[C]∥The 80thShock ＆Vibration Symposium,2009-10

[4] 祝济之,杨志鹏.多维随机振动试验中的互谱控制技术[J].航天器环境工程,2010,27(5): 621-624 Zhu Jizhi,Yang Zhipeng.Cross-spectral control technique in multi-dimensional random vibration test[J].Spacecraft Environment Engineering,2010,27(5): 621-624

[5] 陈颖,田光明,钟继根.典型细长体结构的两点激励振动试验设计[J].航天器环境工程,2013,30(1): 68-71 Chen Ying,Tian Guangming,Zhong Jigen.Dual-exciter vibration test design for a typical slender structure[J].Spacecraft Environment Engineering,2013,30(1): 68-71

[6] 高贵福,王刚,赵保平.一种新的多维随机振动试验控制算法——矩阵微分法[J].强度与环境,2008,35(5): 38-42 Gao Guifu,Wang Gang,Zhao Baoping.A new algorithm for MIMO random test control: matrix differential method[J].Structure ＆Environment Engineering,2008,35(5): 38-42

[7] 贺旭东,陈怀海,申凡,等.双振动台随机振动综合控制研究[J].振动工程学报,2006,19(2): 145-149 He Xudong,Chen Huaihai,Shen Fan,et al.Study on dual-shaker random vibration test control[J].Journal of Vibration Engineering,2006,19(2): 145-149

[8] Underwood M A,Keller T.Testing civil structures using multiple shaker excitation techniques[J].Sound and Vibration,2008,42(4): 10-15

[9] Underwood M A,Keller T.Applying coordinate transformations to multi-DOF shaker control[J].Sound and Vibration,2006,40(1): 14-27

[10] Roukema J C,Altintas Y.Time domain simulation of torsional-axial vibrations in drilling[J].International Journal of Machine Tools ＆Manufacture,2006,46(15): 2073-2085

[11] Underwood M A,Keller T.Rectangular control of multi-shaker systems: theory and practical results[J].Journal of the IEST,2004,47(1): 80-86

[12] Underwood M A,Keller T.Recent system developments for multi-actuator vibration control[J].Sound and Vibration,2001,35(2): 52-58

[13] Underwood M A.Apparatus and method for adaptive closed loop control of shock testing system: United States,5517426[P].1996-05

[14] Underwood M A.Adaptive control method for multi-exciter sine tests: United States,5299459[P].1994-04

[15] Underwood M A.Multi-exciter testing applications: heory and practice[C]//Environmental Sciences and Technology (ESTECH 2002).Anaheim,California,2002-05-01