基于粒子群优化的激光光斑图像增强改进算法

李 莉，秦 勤，李 建

（河南工程学院 计算机科学与工程系，河南 郑州450007）

0 引 言

为了能从红外图像中快速准确地把目标识别出来，需要对模糊的图像进行增强处理。对红外图像进行增强处理前需要进行图像分割提出目标。红外图像是一类特殊的图像，具有强背景、低反差和高噪声等特点，早期的图像分割分为边界和区域方法两大类，基于彩色分量分割和纹理图像分割也广泛被应用。采用 “三阶矩不变”算法，对激光光斑进行图像分割，提取出目标，能够等到更好的效果［1］，但还不能满足某些特定的场合。图像的平均强度和信息熵是评价图像质量的两个重要的参数。平均强度反映的是图像的整体亮度，而信息熵反映的是图像包含的信息量，这两个参数在进行图像增强的过程中是一对相互矛盾的变量。为使得增强的图像的平均强度和信息熵达到某种最优状态，文献 ［2］中提出了一种改进的混合粒子群算法，也就是 “γ－修正”算法，具有灵活的结构，能够较好的解决上述存在的矛盾。为了在对图像进行对比度增强的同时，使背景光照环境更加好，信息量更多，在 “γ－修正”算法的基础上，演化建立了4种数学模型，通过4种数学模型的求解，提出了一种更为严谨科学的 “（a、b、γ）－修正”算法，并应用在激光光斑目标的增强过程中。经过实验表明，该算法能够更加精确，更加合理的平衡上述矛盾。

1 三阶矩不变图像分割

将概率论中的 “矩法”概念引进到图象分割中，提出了 “矩不变阈值分割法”及其相关改进。从统计学角度来讲，可以把原始图像当作二维随机过程中的一个样本，并把样本看作理想图像的模糊视觉；图象分割看作是由样本估计总体的特征，用样本分布来估计总体的分布，变成一个参数估计的问题来处理［3］。矩不变的基本思想是：使阈值分割前后，图像的矩保持不变。假设一幅图像共有n 个像素，f（x，y）是像素的灰度，则定义该图像的p 阶亮度矩如下

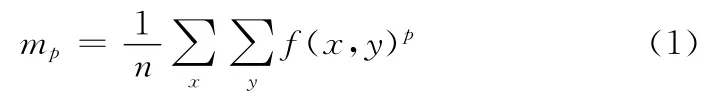
利用直方图统计数据简化计算，设nk为直方图中灰度值为k 的像素个数，则上式可以修改成

若采用二值分割方法，那么分割后的图像仅有z0和z1两个灰度级，并且z0＜z1。低于和高于阈值的像素比例分别用p0和p1表示［4］，那么分割后图像的p阶亮度矩yp可以表示成如下的形式

按照矩不变的思想，可以得到mp＝yp。

由于分割前后的前三阶矩相等，故得到方程组如下

从上述方程组中可以解得

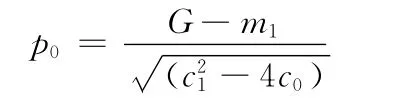
其中

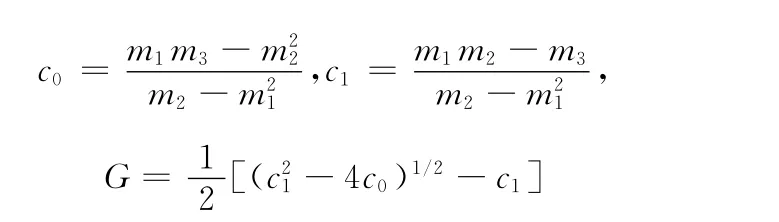
得到p0，再选择合适的t满足式 （5）

式（5）中的t就是要求的分割阈值。若找不到合适的t满足式（5），就选择最接近的灰度值当作分割阈值［5］。最终利用得到的阈值对激光光斑图像进行分割，将图像中灰度小于阈值的像素的灰度置0，灰度大于或等于阈值的像素的灰度保持不变［6］。

2 从“γ－修正”算法中提取数学模型

对一幅图像而言，灰度分布没有任何规律，不能用任何函数来表征灰度分布。“γ－修正”就是通过有规律的修改图像上每个像素点的灰度，从而调整图像上每个灰度的像素的个数，最终使图像的灰度分布呈现为一种近似幂函数的形式，其中γ是幂指数。当幂指数γ在一定范围内变化的时候，图像的灰度分布也随着变化，图像的增强效果也有所变化，且平均强度M 和信息熵E是一对变化相反的变量，所以在进行图像增强的时候，必须同时对这两个变量进行考虑，以达到某种均衡的状态，使图像的整体质量达到最优，这属于多目标优化和决策的问题，故提出一种改进的 “（a、b、γ）－修正”算法。

“γ－修正”算法使图像的灰度分布在整个灰度段即［0，255］上呈现近似幂函数形式。而 “（a、b、γ）－修正”算法比 “γ－修正”算法多引进了两个参数a 和b，分别表示某一灰度段的下限和上限，最终使图像的灰度分布在灰度段［a，b］呈现近似幂函数形式。因为对于同样的γ，不同的a和b将会最终导致不同的灰度分布，进而对图像的平均强度和信息熵产生影响。也就是说，除了幂指数γ，a 和b 的大小，也只有将三者结合起来考虑，才能得到更精确，更严谨的最优解。采用一种改进的粒子群优化算法MPSO，在 “γ－修正”算法的基础上提取4种数学模型：①（a、b、γ）已知模型。当已寻得适合图像最优的a、b、γ的时候，通过此模型得到最终增强的图像；②a、b已知，γ未知模型。给定灰度段［a，b］，求γ使图像平均强度和信息熵达到某种最优状态；③a、b未知，γ已知模型。给定不同的γ，求解是否存在不同的［a，b］使图像平均强度和信息熵达到某种最优状态。验证参数a、b存在的意义和价值；④（a、b、γ）未知模型：求解（a、b、γ），使图像平均强度和信息熵达到某种最优状态［7－9］。

从上述模型中可以看出，“（a、b、γ）－修正”算法实际上是在 “γ－修正”算法的基础上，充分证明参数a、b存在的意义和价值的前提下，通过求解（a、b、γ）未知模型得到最优的（a、b、γ），最后将最优的（a、b、γ）代入（a、b、γ）已知模型得到最终增强的图像。

2.1 （a、b、γ）已知模型

已知：①图像的原始灰度分布（直方图分布），即图像总像素个数N，灰度为i的像素个数为S（i），i＝0，1，2，3，…，255；②幂指数γ；③［a，b］问题：使图像在［a，b］这个灰度段呈现幂函数形式，即

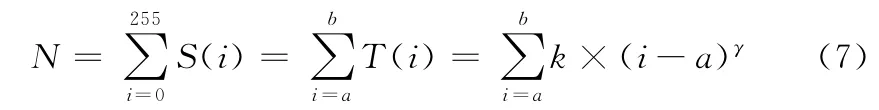
由

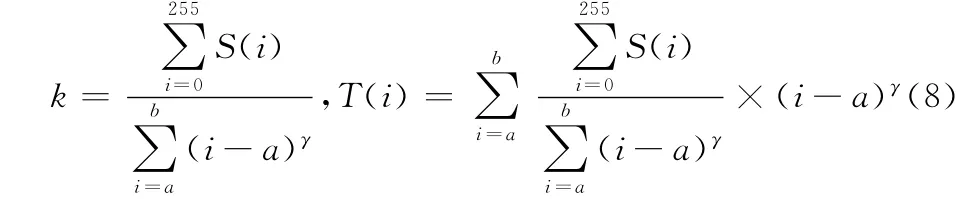
得到最终所需图像的灰度分布T（i），并演变为已知图像的原始灰度分布S（i）和图像的目标灰度分布T（i）。通过①将图像中每个像素按照位置保存在向量V 中；②将向量V 升序排列；③将前T（a）个灰度置为a，接下来的T（a＋1）个灰度置为a＋1，接下来的T（a＋2）个灰度置为a＋2…依次类推，直到分配完毕。就可将图像的原始灰度分布S（i）按照转化为指定的灰度分布T（i）。

2.2 其余3种模型

其余3种模型的最终优化目标相同，只是已知或未知的参数状态不同。已知：

（1）图像的原始灰度分布（直方图分布），即。图像总像素个数N，灰度为i 的像素个数为S（i），i＝0，1，2，

3，…，255；

（2）最终增强图像的灰度分布T（i）如下（a，b已知）

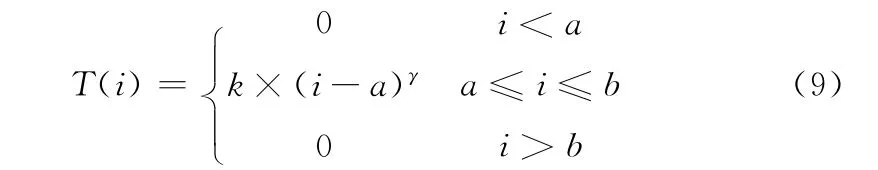
（3）最终增强图像的平均强度为M，熵为E，分别表示如下

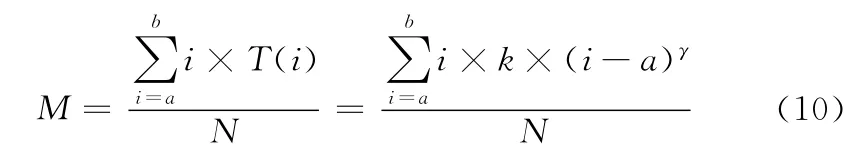
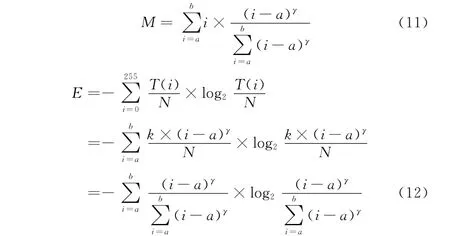
在a、b已知，γ未知模型；a、b 未知，γ已知模型；（a、b、γ）未知模型3种情况下，求解参数使得M 和E 达到某种最优状态。

3 数学模型求解

对于多目标的决策和优化问题，采用多目标规划中的理想点法，先将多目标问题转化为单目标问题，再对单目标利用粒子群算法求解最优值［10－14］。

3.1 理想点法

假若目的是为了让如下N 个指标S1，S2，…，Sn达到最优，而这N 个指标之间可能互相矛盾

式中：x1，x2，x3，…，xn——所需求的且对目标起决定性作用的变量。目的是求得（x1，x2，x3，…，xn）的一组特解，使这N个目标达到一种最优状态。

理想点法是传统的多目标问题解法。假设上述N 个指标，单个目标的最优解分别为T1，T2，T3，…，Tn。显然，T1∩T2∩T3∩…∩Tn＝｛NULL｝。因为各指标之间可能互相矛盾，满足本身最优解的时候，往往不能满足其它指标的最优解。理想点法的思路就是寻求一组特解，使该解对应的目标值与理想目标值的距离最短，就把这组解称为最优解。假设距离用L 表示，按照理想点法的思想，L 可表示为

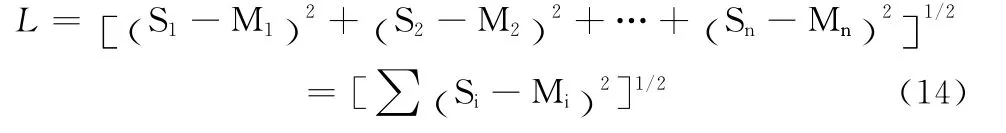
可将多目标问题转化为单目标问题：求Min｛L｝的一组特解。理想点法的关键就是事先能够知道单个目标的最优解。而这种最优解往往可以理解为人为的期望，而不必局限在目标函数的大小范围上。

针对前面提出的数学模型，首先确定2个目标变量S1＝M 和S2＝E 的理想值。理论上说，M 和E 的理想值分别是M 和E 的最大值，通过求取M 和E 的函数表达式的最大值获取，但方法非常繁琐［15］。

通过计算和实验验证：M 是γ的单调递增函数，而E 是γ的单调递减函数。对于任何一幅BMP 格式图像而言，当图像所有像素灰度均为255 的时候图像的平均强度M 最大，Mmax＝255，255可以作为任何图像M 的理想值；而当图像所有灰度的像素个数均相等的时候，图像的熵最大，假设图像总像素总个数为N，那么如果［0，255］每个灰度对应的像素个数相等，用N（i）表示灰度为i的像素个数，可得

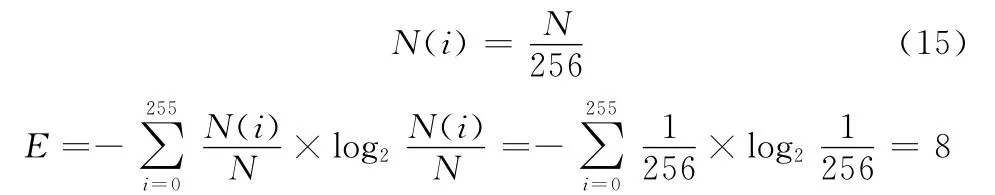
从上述推导可以看出，任何一幅图像的熵最大的值就是8，因此，8可以作为任何图像E 的理想值。按照理想点法的思想，上述数学模型最终转化为在不同的条件下求Min｛L｝

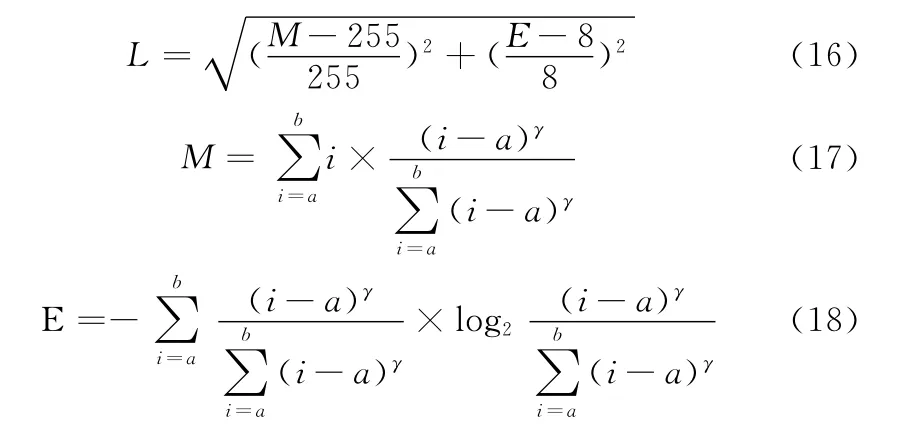
采用目前较为普遍运用的粒子群优化算法去搜索Min｛L｝的最优解。

3.2 粒子群优化算法

这里的粒子群优化（PSO）算法利用了速度－位置搜索模型［16］。处理流程如下：

步骤1 对一群随机粒子进行初始化，设置迭代次数和满足最优解的误差标准；

步骤2 计算得到粒子的目标值；

步骤3 利用个体极值pbest和全局极值gbest 更新自身的速度vi和xi，更新如下所示

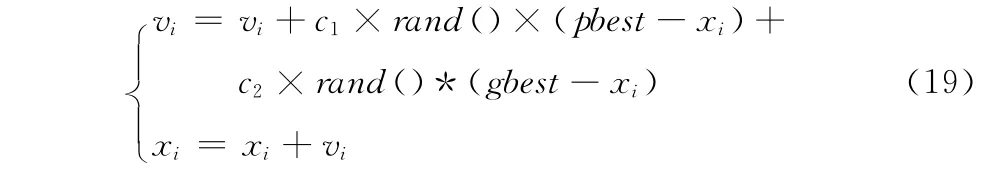
式中：rand（）——一个随机分布函数，它的取值范围均匀分布在（0，1）；c1、c2——学习因子，一般情况下取c1＝c2＝2。

步骤4 通过跟踪个体和全局的极值，并利用式（19）不断的迭代，就可以搜索到最优的解。

4 实验结果及分析

在a和b 已知，γ未知模型中，利用PSO 算法搜索单维解得结果见表1。

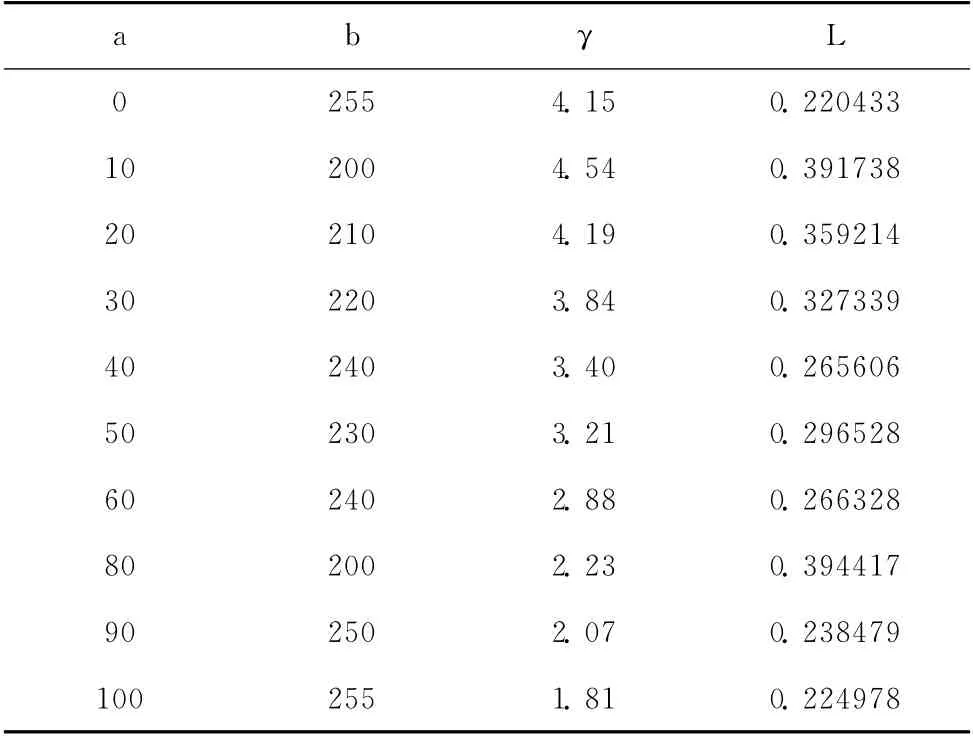
表1 PSO 算法搜索单维解得结果（a和b 已知，γ未知）

在a和b 未知，γ已知模型中，利用PSO 算法搜索二维解得结果见表2。

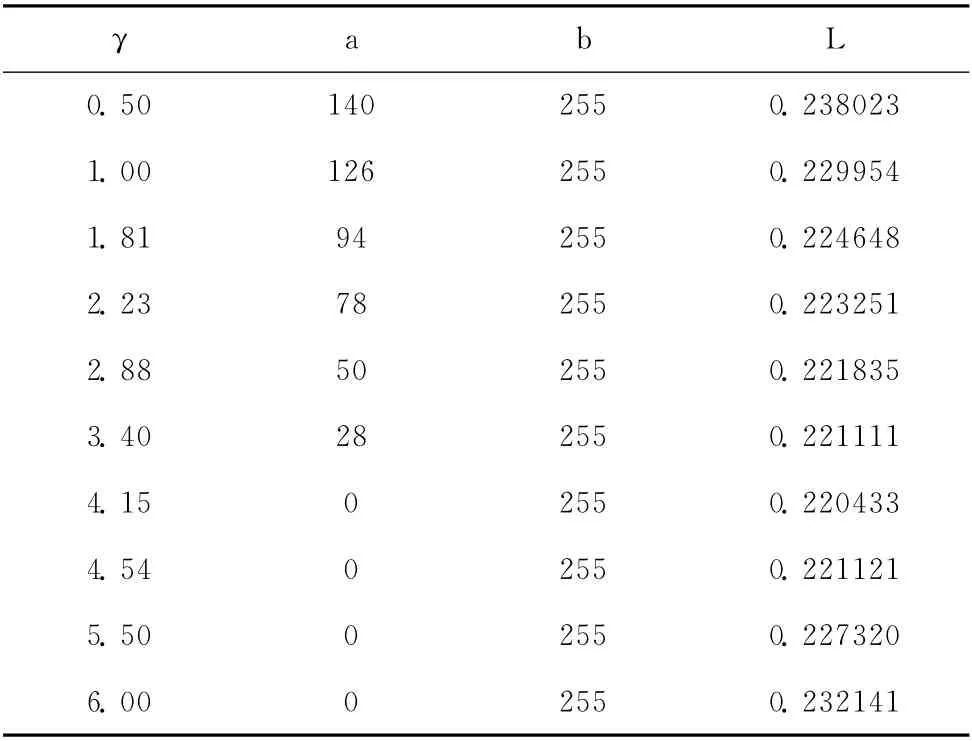
表2 PSO 算法搜索二维解得结果（a和b 未知，γ已知）

在（a、b、γ）未知模型中，利用PSO 算法搜索三维解求得最终的结果是：a＝0；b＝255；γ＝4.15；L＝0.220433。

在（a、b、γ）未知模型中，将已经得到的（a、b、γ）代入（a、b、γ）未知模型中，对远红外激光光斑图像进行增强效果如图1所示。

图1 远红外激光光斑图像进行增强效果

从图1（a）和图1（b）可以看出， “三阶矩不变”算法能较好的将弱光斑目标分割出来，从图1（c）的结果来看，图像得到了较好的增强。增强后的直方图呈指数形式分布，与理论预期的效果保持了一致性。

从表3中可以看出，（a、b、γ）－修正算法比三阶矩不变图像分割的M 和E值分别提高了5.395和1.326倍。对近红外激光光斑图像进行增强效果如图2所示。

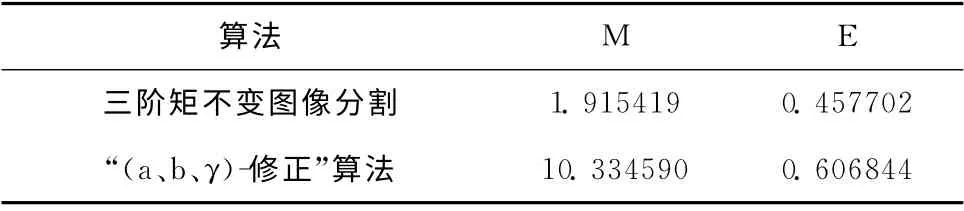
表3 远红外激光光斑图像增强后平均强度和信息熵对比

图2 近红外激光光斑图像进行增强效果

从图2（a）和图2（b）可以看出， “三阶矩不变”算法也能较好的将弱光斑目标分割出来。从图2（c）的结果来看，图像得到了较好的增强。增强后的直方图呈指数形式分布，与理论预期的效果保持了一致性。

从表4中可以看出，（a、b、γ）－修正算法比三阶矩不变图像分割的M 和E 值分别提高了2.458和1.130倍。

表4 近红外激光光斑图像增强后平均强度和信息熵对比

从上边两个实验结果可以看出，相同的a和b，存在最优的γ使得目标函数最优；相同的γ，存在最优的a 和b 使得目标函数最优；存在最优的a、b、γ使得目标函数最优；“（a、b、γ）－修正”算法在一定程度上增强图像。

5 结束语

利用 “三阶矩不变”算法对激光光斑图像进行分割，提取出了目标，在 “γ－修正”算法的基础上引进参数灰度段上下限a和b。在充分验证a 和b 对图像影响的前提下，提出了 “（a、b、γ）－修正”算法，使得 “γ－修正”算法得到进一步内容上的升华和理论上的提高。通过大量实验验证了“（a、b、γ）－修正”算法的理论性，具有很强的灵活性，科学性及其有效性。可以根据需要定义不同的目标函数，最终得到不同程度的增强图像。

［1］NI Qingqing，WANG Hao.The image segmentation by threshold based on gray and intensity invariable ［J］.Journal of Shanghai Normal University （Natural Sciences），2006，35（3）：39－42 （in Chinese） .［倪青青，王昊.基于一阶和二阶亮度矩不变的图像阈值分割的迭代算法 ［J］.上海师范大学学报，2006，35 （3）：39－42.］

［2］Ngai M Kwok，Ha Q P，Member，et al.Contrast enhancement and intensity preservation for gray－level images using multi－objective particle swarm optimization ［J］.IEEE Transactions on Automation Science and Engineering，2009，6 （1）：145－155.

［3］HAN Liming，WANG Botao，CHEN Zhe，et al.A method of measuring roundness of laser beam spot based on digital image processing ［J］.Computer Applications and Software，2011，28 （6）：275－277 （in Chinese） .［韩立明，王波涛，陈喆，等.一种基于图像处理的激光光斑圆度测量方法 ［J］.计算机应用与软件，2011，28 （6）：275－277.］

［4］CAO Junfeng，SHI Jiacheng，LUO Haibo，et al.Image enhancement using clustering and histogram equalization ［J］.Infrared and Laser Engineering，2012，41 （12）：3436－3441 （in Chinese） .［曹军峰，史加成，罗海波，等.采用聚类分割和直方图均衡的图像增强算法 ［J］.红外与激光工程，2012，41 （12）：3436－3441.］

［5］LI Hang，LU Yang，CUI Huijuan，et al.Image quality assessment based on frequency domain of structural similarities ［J］.Journal of Tsinghua University （Science and Technology），2009，49 （4）：559－562 （in Chinese） .［李航，路羊，崔慧娟，等.基于频域的结构相似度的图像质量评价方法 ［J］.清华大学学报，2009，49 （4）：559－562.］

［6］REN Jijun，HE Mingyi.Image segmentation using improved snake model based on particle swarm optimization ［J］.Journal of Image and Graphics，2008，13 （9）：1727－1732 （in Chinese） .［任继军，何明一.基于粒子群优化算法的改进Snake模型的图像分割方法 ［J］ .中国图象图形学报，2008，13（9）：1727－1732.］

［7］LIAO Yanlin，LIU Ye，CAO Jie，et al.A surface enhanced raman scattering spectrum detection system based on fiber devices［J］.Chinese Journal of Lasers，2012，39 （7）：215－219 （in Chinese） .［廖艳林，刘晔，曹杰，等.一种基于光纤器件的表面增强拉曼散射光谱检测系统 ［J］.中国激光，2012，39（7）：215－219.］

［8］LEI Yanmin，ZHU Qidan，ZHONG Xunyu，et al.Study on obstacle detection based on laser range finder ［J］.Computer Engineering and Design，2012，33 （2）：718－723 （in Chinese）.［雷艳敏，朱齐丹，仲训昱，等.基于激光测距仪的障碍物检测的仿真研究 ［J］ .计算机工程与设计，2012，33（2）：718－723.］

［9］ZHANG Yixiong，LI Xiying.Extraction of dumbbell shape object based on GVF and balloon improved model［J］.Computer Engineering and Design，2010，31 （9）：2131－2134 （in Chinese） .［张奕雄，李熙莹.基于GVF和压力Snake模型的哑铃型目标提取 ［J］ .计算机工程与设计，2010，31 （9）：2131－2134.］

［10］Ghita O，Whelan P F.A new GVF－based image enhancement formulation for use in the presence of mixed noise［J］.Pattern Recognition，2010，43 （8）：2646－2658.

［11］XIAO Quan，DING Xinghao，WANG Shoujue，et al.A halofree and hue preserving algorithm for color image enhancement［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2010，22 （8）：1246－1252 （in Chinese） .［肖泉，丁兴号，王守觉，等.有效消除光晕现象和颜色保持的彩色图像增强算法 ［J］ .计算机辅助设计与图形学学报，2010，22（8）：1246－1252.］

［12］ZHANG Rong，FENG Bin，SUN Jun.Analyzing SELDI－TOF mass spectral data based on QPSO－SVM algorithm ［J］.Computer Applications and Software，2011，28 （1）：57－60 （in Chinese） .［张蓉，冯斌，孙俊 .基于QPSO－SVM 算法的SELDI－TOF质谱数据分析 ［J］.计算机应用与软件，2011，28 （1）：57－60.］

［13］MA Shiyou，FU Zhiwei，WANG Xiaodong，et al.Gray image enhancement algorithm based on histogram equalization and power transform ［J］.Computer Applications and Software，2013，30 （4）：261－263 （in Chinese） .［马士友，付致伟，王晓东，等.基于直方图均衡和幂次变换的灰度图像增强算法 ［J］.计算机应用与软件，2013，30 （4）：261－263.］

［14］KANG Changqing，YUAN Lei，HUA Li，et al.A novel Hessian matrix enhancement algorithm for angiography images［J］.Computer Engineering ＆Science，2012，34 （10）：104－107 （in Chinese） .［康长青，袁磊，华丽，等.一种新的血管造影图像Hessian矩阵增强算法 ［J］.计算机工程与科学，2012，34 （10）：104－107.］

［15］WANG Xuewei，WANG Shili，LI Ke.Infrared image enhancement based on pseudo median filter and wavelet transformation［J］.Laser ＆Infrared，2013，43 （1）：90－93 （in Chinese）.［王学伟，王世立，李珂.基于伪中值滤波和小波变换的红外图像增强方法 ［J］.激光与红外，2013，43 （1）：90－93.］

［16］ZHANG Xiuhua，YANG Kuntao.Image enhancement based on maximum entropy principle and gray－level transformation ［J］.Opto－Electronic Engineering，2007，34 （2）：84－87 （in Chinese） .［章秀华，杨坤涛.基于最大熵原则和灰度变换的图像增强 ［J］.光电工程，2007，34 （2）：84－87.］