基于机器学习的超宽带NLOS鉴别方法

李伟杰，张霆廷，张钦宇

（哈尔滨工业大学 深圳研究生院 通信工程研究中心，广东 深圳518055）

0 引 言

在无线定位技术中，基于TOA（time of arrival）估计的超宽带定位技术能够利用它极高的时域分辨力，抗多径能力强，穿透能力强等特点，实现高精度定位［1］。实际定位中NLOS环境（non line of sight）是误差的主要来源之一。第一，由于NLOS引起的多径效应引起的直达分量会被误检，第二，超宽带脉冲介质中传播时会引起附加的时延，使得TOA 估计值会大于真实值。如果使用带有NLOS 的TOA 估计值进行定位将严重影响定位性能，在实际定位环境中对NLOS 进行鉴别和误差消除能够有效提高定位精度［2］。

文献［3－5］从蜂窝网络领域研究了NLOS的鉴别技术，文献［3］基于扩展卡尔曼滤波角度出发，通过对新息序列的预测来进行NLOS鉴别。文献［4］根据多次测量结果求得TOA 的方差，建立了不同的假设检验模型实现NLOS 鉴别。文献［5，6］说明利用接收信号的多径分量与能量的关系可以更有效进行NLOS鉴别，文献［7］根据信号特征参数在不同信道具有不同的分布进行鉴别。

NLOS消除方面，存在两种方法：第一，根据TOA 估计值的修正，NLOS会使TOA 带来正偏差，估计出这个正偏差后可以直接对TOA 进行修正［8］。第二，定位算法层面上的消除，在鉴别出NLOS的结果后赋予不同的权重，在定位算法进行消除［9］。

现在NLOS鉴别和消除存在的主要问题有，鉴别和消除都基于不同理论模型，实际应用场景一些先验难以获取，如信道统计特性，特征参数概率密度函等。本文基于实测数据对广泛采用的参数法［7］的NLOS 鉴别方法进行验证，并参考文献［10］的方法采用一种基于非参数的机器学习方法进行NLOS鉴别，对机器学习的训练参数的选取进行分析，实现了更高的鉴别率。在此基础上对实测数据进行NLOS消除，并对不同的NLOS鉴别率对定位性能的影响进行了分析，文章实现了一种通用的NLOS鉴别模型和消除算法。

1 基于特征参量的NLOS鉴别

1.1 信号的特征参数

设计接收到的信号记为h（t）。

（1）峭度（kurtosis）

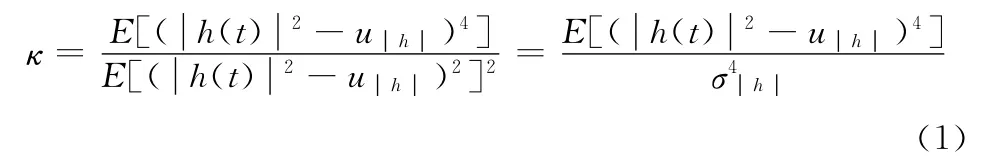
如式（1）所示，它可反映数据集中分布的陡峭程度，一般地，信号的峭度值越大，说明数据中存在较大峰值且下降明显，能量比较集中，峭度值较小，说明数据分布较为平坦，能量较为分散。

（2）超量时延（mean excess delay，MED）

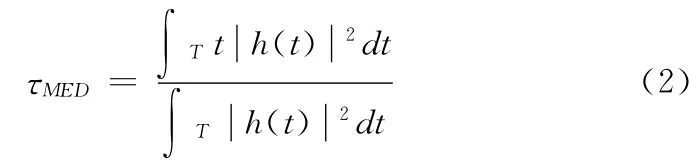
（3）均方根时延（root mean quare delay spread，RMS）

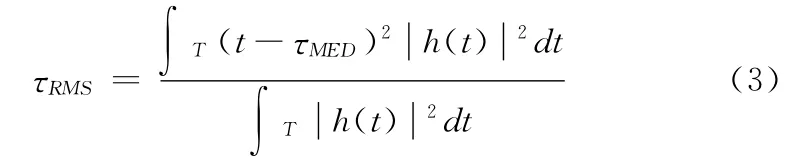
峭度提供了多径分量的幅度统计信息，但不包含时延信息，超量时延式（2）和均方根时延式（3）体现了多径分量的时延特征，一般来说，NLOS 下的平均超量时延要比LOS时大，RMS时延扩展比LOS更严重。

（4）峰值能量比

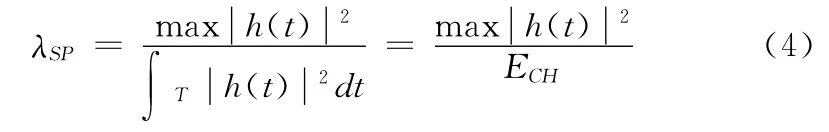
式（4）定义了最强路径与信号能量比，利用多径能量差异性进行NLOS鉴别。

（5）幅度

（6）能量

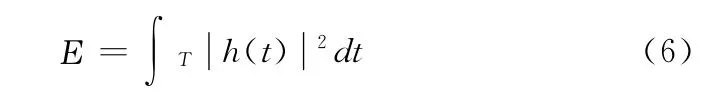
在相同距离下，信号经过NLOS障碍物后的幅度式（5）和能量式（6）比LOS情况下的幅度和能量要小。

（7）采样数据均值

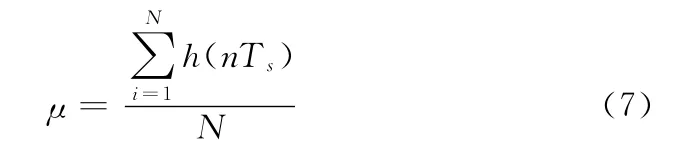
（8）采样数据方差

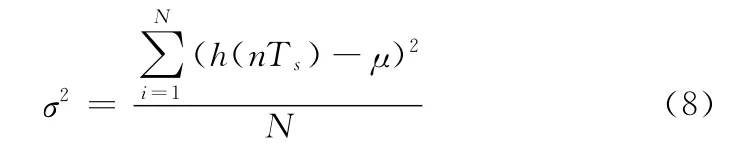
方差式（8）反映了采样数据的集中程度，NLOS情况下的采样数据会比较分散。

1.2 参数方法

文献［7］研究表明UWB信号通过IEEE 802.15.4a信道后，特征参数Kurtosis，MED，RMS的概率密度函数成对数正态分布且存在差异性。从而将NLOS鉴别问题转化为似然比检验问题，在不同信道模型下鉴别的成功率见表1。

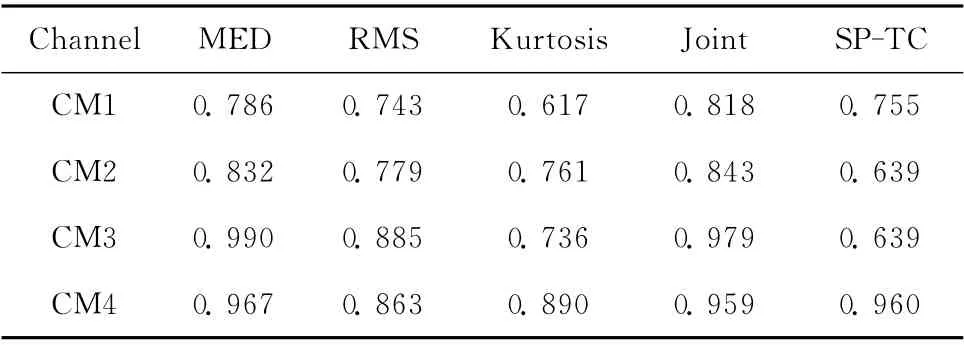
表1 参数法鉴别率

表1体现出参数法具有极高的NLOS鉴别率高，实际应用中该方法是否通用需要进行验证。我们采用Time－Domain公司的产品PulsOn 410［11］进行数据采集，该产品发出的UWB 信号的带宽为2.2GHz，中心频率在4.3GHz，采样频率为60ps，具有极好的抗干扰能力和测距精度，它采用Lead Edge Detection的TOA 估计算 法［12］，在室内进行了数据采集如图1所示，该图为中国典型室内居住环境，外墙厚度为18cm，隔墙厚度为12cm，墙视为NLOS障碍物，在此环境建立了1000个LOS和NLOS信号的数据库。并对这些数据的信号特征进行了统计，图2统计了它们的MED，RMS，Kurtosis分布。

图1 测量环境

对LOS 和NLOS 情况下实测数据的特征参数进行统计，根据虚警概率Pfa＝2%设定NLOS鉴别的门限值，鉴别的成功率见表2。图3对比了实测数据和理论数据采用参数法进行NLOS 鉴别的准确率，检测概率定义为Pc＝P（NLOS｜NLOS），虚警概率定义Pfa＝P（NLOS｜LOS）。

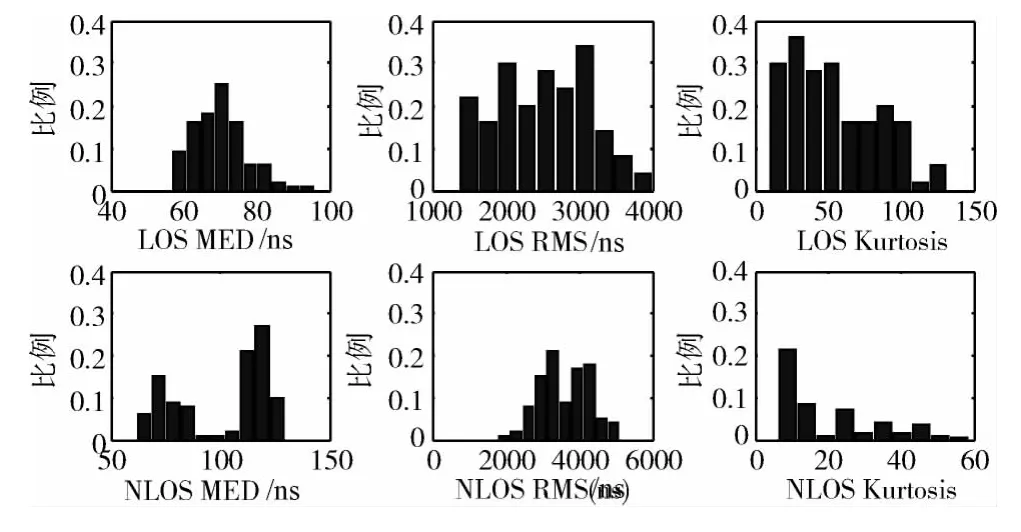
图2 LOS和NLOS下MED，RMS，Kurtosis分布对比

表2 实测数据鉴别率

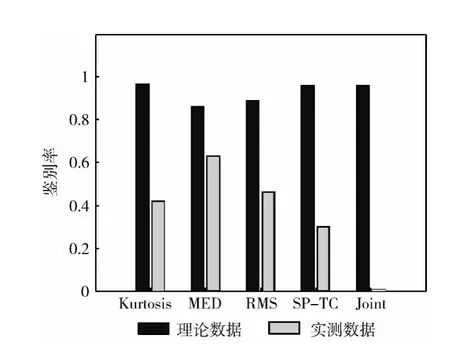
图3 仿真数据和实测数据的鉴别率比较

本节实验表明UWB 信号在室内传播中特征参数的分布并不服从函数分布。用基于门限的参数法进行NLOS鉴别，鉴别准确率远低于文献［7］的结果，参数法在该典型室内中进行NLOS鉴别失效。

2 基于LS－SVM 的NLOS鉴别

2.1 LS－SVM（least square－support vector machine）介绍

由第1节可知，实际环境中采用参数法进行NLOS鉴别方法鉴别率低，在这种参数的总体分布类型未知条件下，应该采用非参数的方法进行NLOS鉴别［13］。

基于机器学习的LS－SVM 是非参数的分类方法，它的优点有：①对于线性不可分的情况，通过映射算法转化为高维特征空间使其线性可分；②SVM 学习问题可以表示为凸优化问题，可以利用已知的有效算法求解目标函数的全局最小值。SVM 的优点使得它能成为非参数分类方法的首先技术，利用SVM 进行NLOS分类学习的目标是构造一个判别函数（分类器），将数据尽可能正确地分类，其示意图如图4所示。

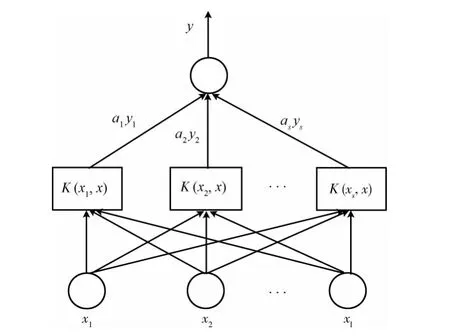
图4 LS－SVM 分类器

该图对输入向量为x＝（x1x2…xl），即对l个信号进行分类，xi∈RN为一个UWB 信号提取的N 个特征参数，S个支持向量通过核函数K（x，x）对输入进行非线性变换，输出y＝（y1y2…yl）取值为1和－1用于表示LOS和NLOS情况。更深入的内容LS－SVM 原理介绍参见文献［14］。

2.2 基于LS－SVM 的NLOS鉴别性能

根据1.1小节所选的参数作为训练参数，对数据进行划分，用训练数据（20%）训练出相关的参数，再将测试数据（80%）测试下分类器的效果，结果见表3。

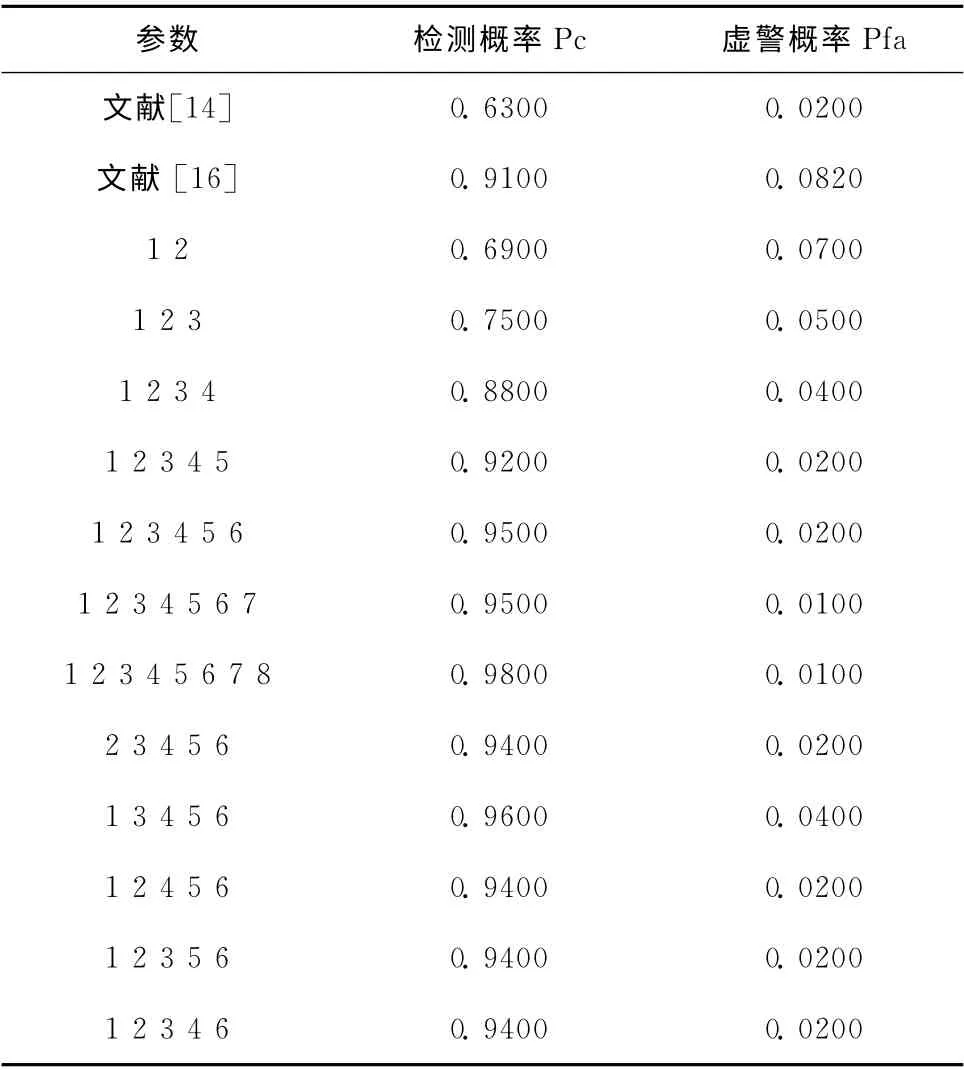
表3 不同特征参数的鉴别率

本节仿真说明：①采用多个参数进行联合检测时能够使性能提高很多；②跟参数法鉴别的方法相比，在相同的虚警概率下，基于LS－SVM 的NLOS鉴别方法在检测概率高25%以上；③采用全部特征参数（MED，RMS，Kurtosis，幅度，能量，SP－TC，均值，方差）进行机器学习，训练出来的分类器具有较优的性能，检测概率可以达98%，虚警概率只有1%，相比较现有方法而言在性能上有较大提高。

2.3 NLOS误差消除

图5为LOS和NLOS情况下的测距误差统计，从图中可知NLOS情况下误差都偏大，这是由于UWB 信号通过障碍物的附加时延引起的。

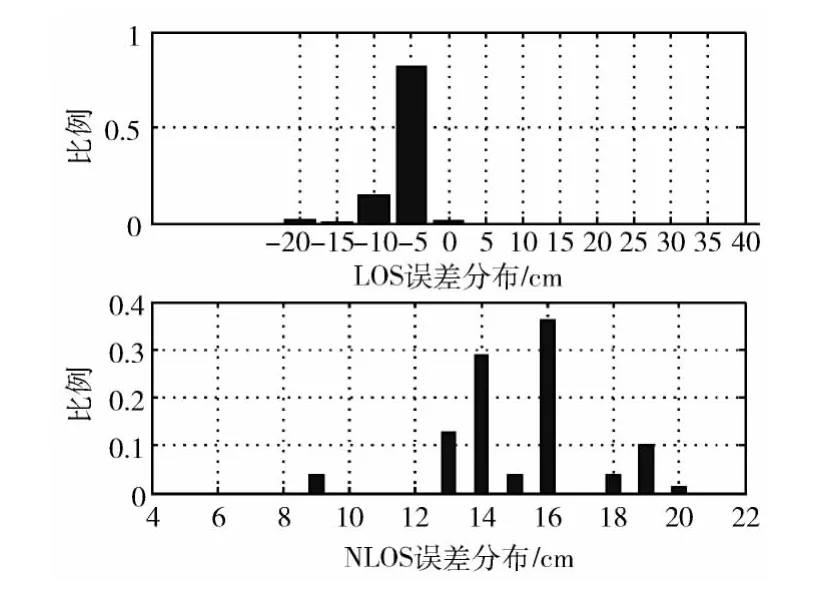
图5 误差统计

根据LOS和NLOS误差的统计分布，可以采取如下方法进行NLOS消除，LOS情况下采取＝＋Δ1，NLOS情况下采取＝－Δ2。误差消除前和消除后的概率分布曲线如图6所示。

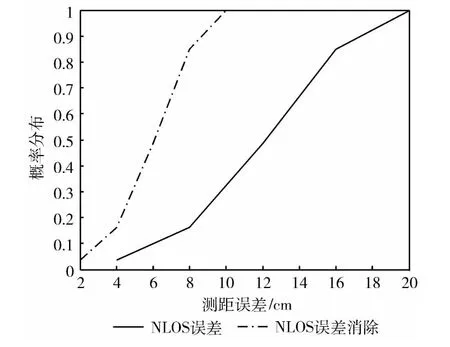
图6 误差消除

定位性能如图7所示，仿真条件说明：①定位区域为半径R＝10m 的圆内，锚节点数量为N＝10在圆上均匀分布；②目标节点与10个锚节点都属于NLOS情况；③测距误差根据实测数据的误差建立的数据库中随机选取；④鉴别后对于LOS采用＝＋Δ1，对于NLOS采用误差消除＝－Δ2；⑤在④的基础上采用Taylor算法处理［15］。

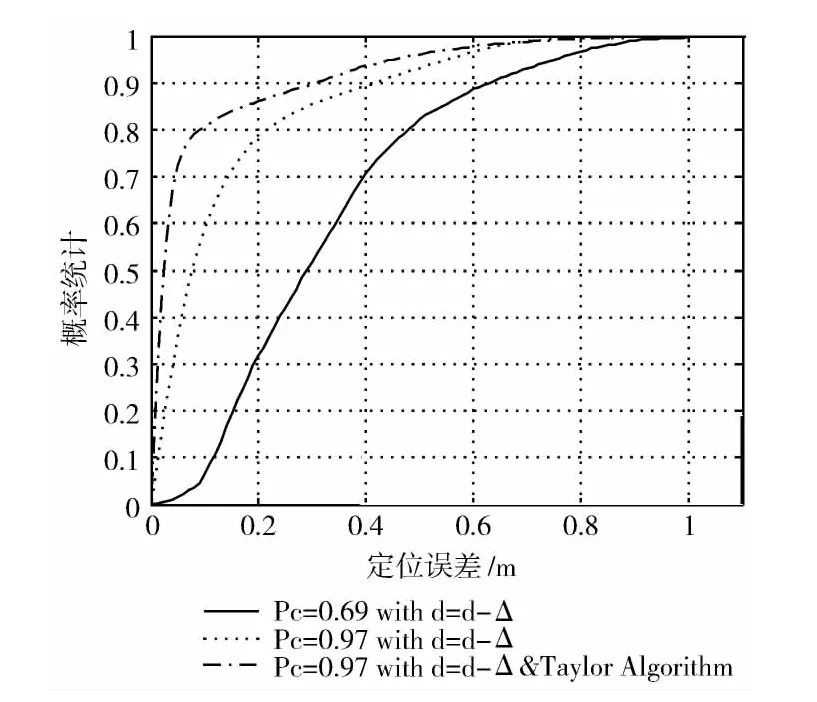
图7 定位性能

从图7可以看出，经过NLOS鉴别后，再进行误差消除，效果明显。定位结果在0.5m 以内的误差经过消除前在占80%，经过消除后95%，性能提升15%。

3 结束语

传统的NLOS鉴别方法通常采用IEEE 802.15.4a信道模型，该模型与实际环境相比存在较大的差异，利用该模型实现的NLOS鉴别方法在实际场景中出现较低的鉴别率，我们的实验从接收到的UWB 信号提取特征参数进行机器学习来实现NLOS 鉴别，研究表明提取的特征参数越多，鉴别率越高。这种非参数的NLOS 鉴别方法与信道独立，不需要先验知识，鉴别率高，适用范围广。在鉴别的基础上，根据先验统计进行误差消除，可以有效提高定位精度。该文章能有进行NLOS鉴别，为实现室内高精度定位的实现提供了理论基础。

［1］Gezici S，Poor H V.Position estimation via ultra－wide－band signals［J］.Proceedings of the IEEE，2009，97 （2）：386－403.

［2］Qi Y，Kobayashi H，Suda H.Analysis of wireless relocation in a non－line－of－sight environment［J］.IEEE Transactions on Wireless Communications，2006，5 （3）：672－681.

［3］Yu K，Guo Y J.NLOS error mitigation for mobile location estimation in wireless networks ［C］／／IEEE 65th Vehicular Technology Conference.Spring，2007：1071－1075.

［4］Schroeder J，Galler S，Kyamakya K，et al.NLOS detection algorithms for ultra－wideband localization ［C］／／4th Workshop on Positioning，Navigation and Communication，2007：159－166.

［5］DIAO X，Guo FHAB.A method distinguishing line of sight（Los）from non－line of sight（Nlos）in CDMA mobile communication system：European Patent EP 1469685［P］.2008－02－20.

［6］Rabbachin A，Oppermann I，Denis B.ML time－of－arrival estimation based on low complexity UWB energy detection ［C］／／IEEE International Conference on Ultra－Wideband，2006：599－604.

［7］Ismail G，Chia－Chin C，Fujio W，et al.NLOS identification and weighted least－squares localization for UWB systems using multipath channel statistics ［J／OL］.EURASIP Journal on Advances in Signal Processing.http：／／asp.eurasip journals.com／content／2008／1／271984，2008.

［8］Khodjaev J，Park Y，Malik A S.Survey of NLOS identification and error mitigation problems in UWB－based positioning algorithms for dense environments［J］.Annals of Telecommunications－Annales Des Télécommunications，2010，65 （5－6）：301－311.

［9］Jiao L，Xing J，Zhang X，et al.LCC－Rwgh：A NLOS error mitigation algorithm for localization in wireless sensor network［C］／／IEEE International Conference on Control and Automation，2007：1354－1359.

［10］MaranòS，Gifford W M，Wymeersch H，et al.NLOS identification and mitigation for localization based on UWB experimental data［J］.IEEE Journal on Selected Areas in Communications，2010，28 （7）：1026－1035.

［11］Time Domain.Data sheet［EB／OL］.［2012－06－10］.http：／／www.timedomain.com／datasheets／320－0289D%20P410%20Data%20Sheet.pdf.

［12］Time Domain.Ranging and communication application programming interface specification［EB／OL］.http：／／www.timedomain.com／datasheets／320－0282E% 20RCM% 20API% 20Specification.pdf，2012.

［13］Wasserman L.All of nonparametric statistics ［M］.NY：Springer New York，2006.

［14］Suykens J A K，De Brabanter J，Lukas L，et al.Weighted least squares support vector machines：Robustness and sparse approximation ［J］.Neurocomputing，2002，48（1）：85－105.

［15］Zhang H，Yu M，Cui X，et al.An improved Taylor series based location algorithm for IEEE 802.15.4achannels［C］／／IEEE Pacific Rim Conference on Communications，Computers and Signal Processing，2011：499－503.