圆形黄土地铁隧洞暗挖法地表沉降简化解析算法

周 磊，党发宁

(西安理工大学岩土工程研究所，陕西西安710048)

在地铁施工过程中，地面沉降是关注的主要问题之一。沉降一般会对地面建筑和地下管线造成难以修复的破坏，影响人民生命财产安全。国内外对地面沉降的研究主要集中在地表沉降规律预测方法上。预测地表沉降规律的方法有经验预测法、数值模拟预测法、解析理论法、专家系统和灰色理论预测法等［1－2］。

经验预测法是先用数学的方法处理在现场得到的监测数据，再用数学表达式表示出沉降规律，选择较适宜的预测公式对地表沉降规律进行分析，从理论和经验的角度来推测地表最大沉降量和沉降分布规律，比较著名的是Peck公式法。

数值分析方法可将较多的影响因素考虑在内，理论也较明确，所以它的应用得到了迅速发展［3－5］。土层在受隧道开挖扰动后，自身的位移在某种趋势下逐渐发展，而这个过程往往又有一定的不确定性。从数学的角度描述该过程，便可以采用灰色理论预测法。专家系统作为一个新思路对预测隧道开挖地层变形问题提供了很大的帮助。但这种方法自身也存在着一些缺点，如模型复杂、考虑因素多等。因此，到目前为止，此方法还处在最初的研究阶段，离实际的工程应用还有一段距离。

解析法中，林存刚［6］等基于 Mindlin解积分求得盾构掘进时切口附近推力和对周围土体的摩擦力;魏纲［7］通过采用两圆相切的土体损失模型建立了能将Park模型和Loganathan模型包括在内的土体移动模型;Verruijt 用张量法推导出饱和粘土层中隧道施工所引起地层移动的应力函数;Bobet［9］给出极坐标下饱和土体中浅层隧道施工导致地层变形的弹性解;Chou和Bobet［10］推导出了饱和粘土中浅层隧道开挖地层的变形计算公式;Park［11］提出不同地层变形模式下隧道施工导致地层变形的解。

本文通过简化隧洞开挖后的受力条件，寻求能从弹性力学理论方面解答该类问题的方法，得出理论解答。再与数值解答和实际的沉降监测数据比较分析，验证本文方法的有效性。

1 沉降计算理论介绍

1.1 Peck公式简介

Peck公式是美国科学家Peck在采矿工程中提出的位移估算方法。他认为因隧道施工造成的沉降槽的形状近似于正态分布曲线，并给出估算地表横向变形规律的公式:

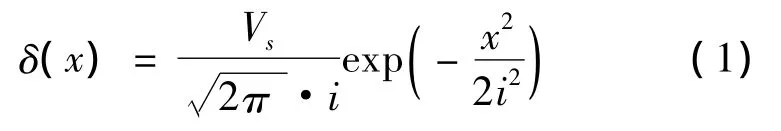
式中:δ(x)为地表横向距离中心线为x处的沉降量;i为曲线上反弯点处的横坐标;x为距隧道中心线的距离;Vs为沉降槽体积，也称地层损失量(推进每米)。

后人在Peck公式的理论基础上进一步研究。美国学者Cording推导出沉陷槽的宽度B和i的关系为:B=5i。Attewell［12］提出沉陷槽宽度系数 i的修正公式为，式中:k、n为常数，H 为隧道轴线埋深，其他参数意义同上。同济大学侯学渊等提出考虑到固结因素的 Peck修正公式:S(x，t)=为隧道顶部土体渗透系数的加权平均值，其他参数意义同上。

1.2 “小孔口问题”的简化及计算

本文研究黄土地区采用暗挖法施工圆形隧道对地面造成的影响。应用弹性力学中“小孔口问题［13－14］”的解答。所谓“小孔口问题”即孔口的尺寸远小于弹性体的尺寸，并且孔边距弹性体的边界比较远(约大于1.5倍的孔口尺寸)。孔口应力集中具有局部性，一般孔口的应力集中区域约在距孔边1.5倍孔口尺寸的范围内。因此，可将某些隧道开挖问题简化成“小孔口问题”。在弹性力学中有如图1(a)所示左右边受力为q1，上下边受力为q2的“小孔口问题”的解答。通过荷载分解，可将其转化为如图1(b)和图1(c)所示的两部分解答。

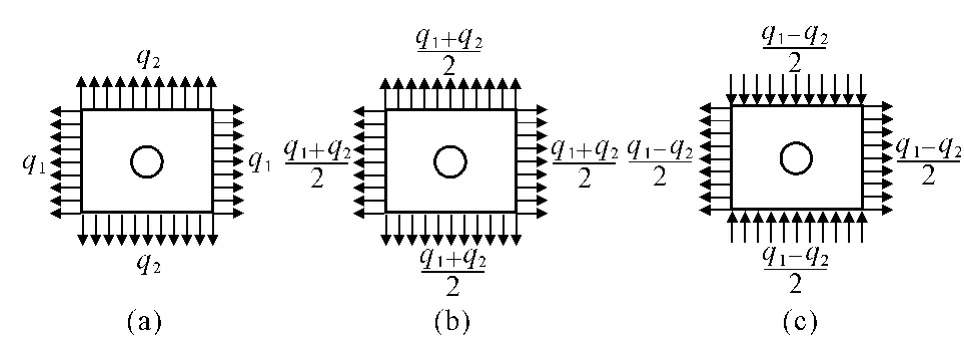
图1 弹性力学中“小孔口问题”的荷载分解图

图1(b)部分的应力解答如式(2)所示，图1(c)部分的应力解答如式(3)所示。

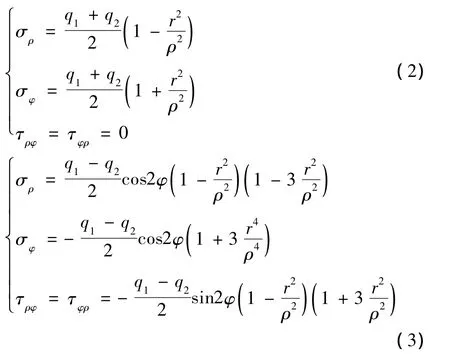
而隧道在实际开挖过程中受力情况可近似简化成如下形式:上下边的受力可简化成隧道圆心处在开挖前所受的土压力γh(h为隧道圆心到地面的距离)，左右边的受力简化为k0γh(k0为侧压力系数)。即q1=－k0γh、q2=－γh，则可应用式(2)和式(3)的解答。

把式(2)和式(3)的解答相加，代入极坐标平面应变问题的物理方程ερ=可得孔径口附近的应变ε，理ρ论上可通过公式求得从r到b范围内土体的变形量，从而可以确定变形后隧洞的半径。但实际上表达式很复杂，几乎不能求解。为了简化计算，假定孔内土体因开挖所产生的应变均匀且等于孔边应变εr，整个土层不受开挖影响，则隧道变形后半径r'=r－εrr。则单位长度隧洞变形后的体积为由此可求出单位长度隧洞体积的收缩量V=πr2×1－V'。

由式(1)可推出:

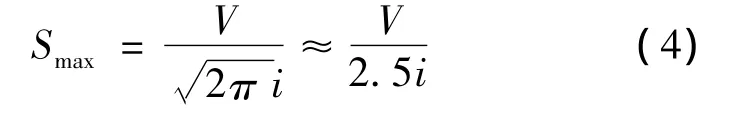
式中:Smax为隧道中心线处的地表最大沉降量(m);V为隧道单位长度体积的收缩量;i为地表沉降槽宽度系数，即沉降槽曲线反弯点至隧道中心线的水平距离。

i可通过经验公式求得:

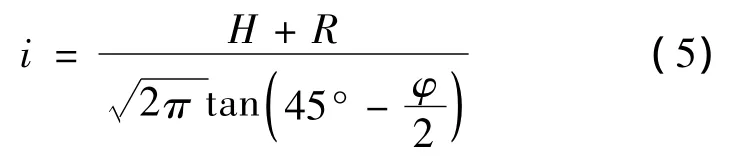
式中:H覆土厚度(m);R为圆形隧洞半径;对于矩形结构R=0.29(h+b)，对于其他非圆形为截面积)。

通过式(4)就可以求出隧洞开挖地面沉降槽最大深度的弹性解答。

2 算例分析

2.1 工程实例分析

西安市地铁一号线某黄土区间隧道［15］长774.597 m，采用盾构法施工。洞顶最大埋深约为16 m，隧洞直径约8 m。为方便计算，隧洞洞顶埋深取为16 m，直径取为8 m。

区间范围内，地表一般均分布有厚薄不均的全新统杂填土(0.7 m ～1.9 m)和素填土(0.7 m ～5.1 m)、其下为上更新统风积新黄土(0.5 m ～5.5 m)、饱和软黄土(2.5 m ～10.3 m)、残积古土壤(3.2 m～5.5 m);再下为中更新统风积老黄土(3.3 m ～9.9 m)、冲积粉质黏土(最大厚度19.4 m)、粉土、细砂、中砂(0.7 m ～3.5 m)及粗砂等。

同样为简化计算，将围岩视为隧道所在土层的单一地层，地层土体参数取值如表1所示。

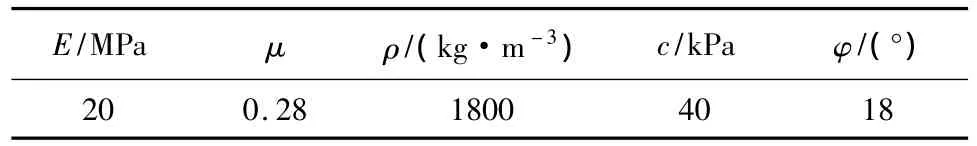
表1 土体参数表

用上述简化的“小孔口问题”方法，计算得到单位长度的黄土地铁隧道施工引起的隧洞变形量是0.7 m3。由于假定了隧洞的变形量等于地面沉降量，所以单位长度地面沉降槽的体积也是0.7 m3。通过公式(4)算得沉降槽的最大深度Smax=25.64 mm。

2.2 数值模拟分析

本文用ABAQUS商业软件建立了上节的黄土地铁隧道三维数值计算模型［16］，模型长100 m，宽40 m，高40 m。隧洞圆心在xy平面形心处。土体参数取值见表1。模型整体只受自身重力作用。底面边界约束为全约束，四周均为法向约束，上表面为自由面。隧洞一次性全断面开挖，不考虑支护。

经计算，沉降槽曲线符合Peck公式规律，沉降槽最大深度为52.66 mm。即图2中圆点所示位置。

图2 隧道开挖引起地层竖向位移变化图

2.3 结果对比分析

分别取弹性解析计算和数值模拟的11个点的沉降值，与实测沉降值分别绘制成沉降槽曲线进行对比分析，如表2和图3所示。

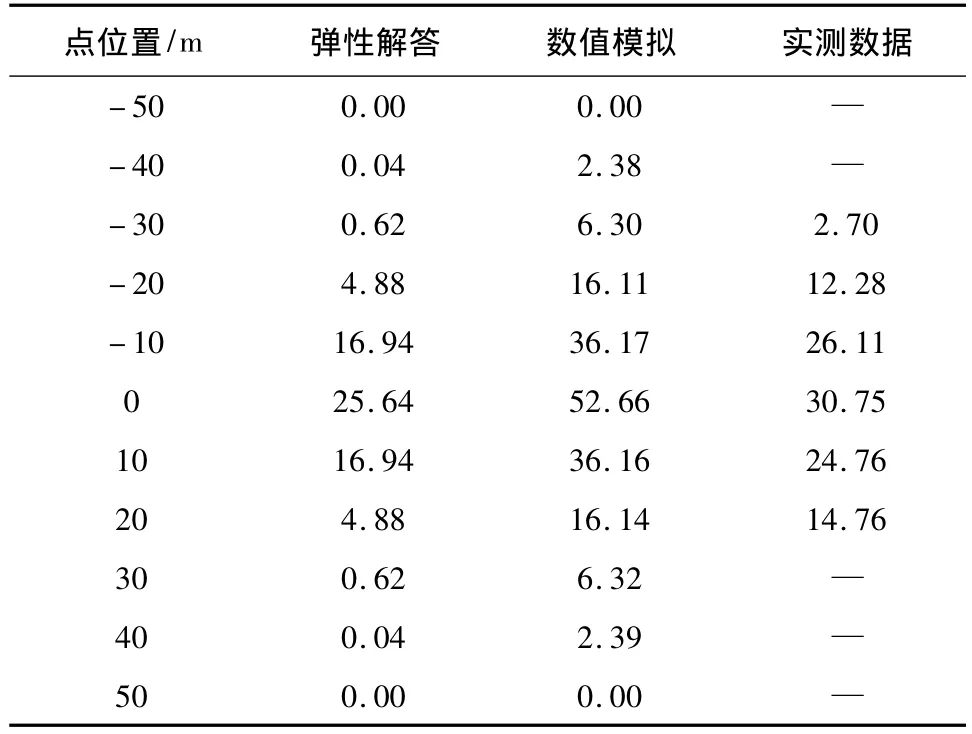
表2 弹性解析解答、数值模拟和实测的沉降值单位:mm

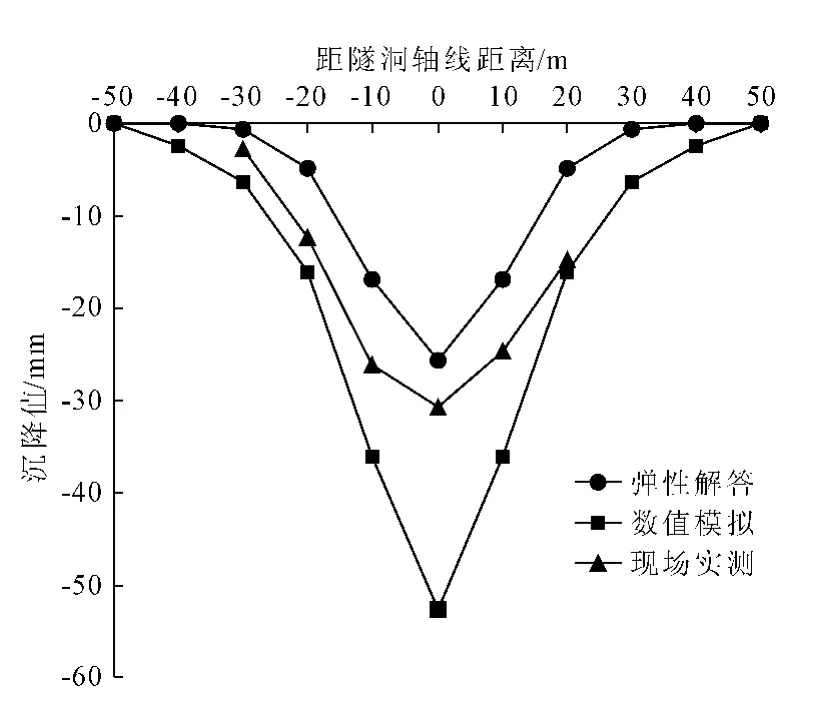
图3 弹性解答、数值模拟和实测的沉降槽曲线图

从图3可以看出，在沉降槽两侧的区域，弹性解答、数值模拟和现场实测的沉降槽曲线在形状上类似。弹性解答的值最小，现场实测的值其次，数值模拟的值最大。考虑到现场实测和数值模拟在沉降上的时间效应的影响，弹性解答偏小较为容易理解。

3 结论

本文通过简化圆形隧道开挖受力条件，用弹性理论方法和数值模拟方法计算了沉降槽深度和沉降槽曲线，得出以下结论:

(1)圆形隧道开挖过程中，土层受力会发生变化，把这种情况看成是“小孔口问题”进行简化计算，简化后地层损失率为1.4%，符合黄土地区地层损失率不大于2%的规律，说明用这种方法简化解析计算圆形隧道地层损失率是可行的。

(2)开挖圆形隧道，弹性解答和数值模拟的沉降槽的最大深度分别为25.64 mm和52.66 mm，而实测沉降槽的最大深度为30.75 mm。弹性解答比实测值小16.62%，数值模拟比实测值大71.25%。弹性解答和实测值较为接近，由于时间效应对数值模拟的影响要比实测明显得多，所以大71.25%可以接受。现实中隧道开挖所引起的土层应力的变化是非常复杂的，几乎不能用理论知识解答。所以，这种简化算法具有一定的现实意义。

［1］阮 松.地铁车站浅埋暗挖法施工引起沉降的控制措施研究［D］.北京:北京交通大学，2007.

［2］于晓曦.沉降预测的三种方法［J］.建筑技术开发，2004，31(5):32-33.

［3］李继升.北京地铁浅埋暗挖法施工引起地表沉降规律的研究［D］.北京:中国地质大学，2012.

［4］邓聚龙.灰色预测与决策［M］.武汉:华中理工大学出版社，1992.

［5］傅 立.灰色系统理论及其应用［M］.北京:中国科学技术文献出版社，1991.

［6］林存刚，张忠苗，吴世明，等.软土地层盾构隧道施工引起的地面隆陷研究［J］.岩石力学与工程学报，2011，30(12):2583-2592.

［7］魏 纲.盾构施工中土体损失引起的地面沉降预测［J］.岩石力学，2007，28(11):2375-2379.

［8］Verruijt A.A complex variable solution for a deforming circular tunnel in an elastic half-plane［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1997，21(2):77-89.

［9］Bobet A.Analytical solutions for shallow tunnels in saturated ground［J］.Journal of Engineering Mechanics，2001，127(12):1258-1266.

［10］Kyung－Ho Park.Analytical solution for tunneling-induced ground movement in clays［J］.Tunnelling and Underground Space Technology，2005，(20):249-261.

［11］Loganathan N，Poulos H G.Analytical prediction for tunneling-induced ground movements in clay［J］.Journal of Geotechnical and Geoenvironmental Engineering，1998，124(9):846-856.

［12］Attewell P B，Yeates J，Selby A R.Soil Movements Induced by Tunneling and Their Effects on Pipelines and Structures［M］.London:Chapman and Hall，1986.

［13］徐芝纶.弹性力学简明教程［M］.北京:高等教育出版社，1980.

［14］吴毓熙.应用弹性力学［M］.上海:同济大学出版社，1989.

［15］佘方涛，韩日美，刘 庚，等.西安地铁双线隧道地表沉降他预测模型研究［J］.防灾减灾工程学报，2011，31(5):561-566.

［16］费 康，张建伟.ABAQUS在岩土工程中的应用［M］.北京:中国水利水电出版社，2010.