基于果蝇算法优化BP神经网络的齿轮箱故障诊断

祁丽婉，梁庚，童国炜

（华北电力大学控制与计算机工程学院，北京 102206）

随着社会的发展，人类对能源的需求持续攀升。伴随着传统能源逐渐枯竭和价格的不断提高，能源供求矛盾不断突出，而风能是一种无环境污染、可再生的的清洁能源，风力发电近年来也得到了世界各地的研究和重视[1-2]。据统计，可供中国开发利用的风能资源约十亿千瓦[3]。在我国政府的高度重视下，至2013年我国的风机能源装机量占世界风机能源装机量的一多半[4]。

风力虽是清洁能源，但风力发电大多工作环境恶劣，机组常处于偏远地带、容易遭破坏且维修不便。随着风电单机容量的增大，加之恶劣的工作环境，机组运行的安全性和可靠性受到影响。研究表明，风力机组主要故障是振动故障，而风力机组的振动故障主要在于传动系统，主要包括主轴、轴承、齿轮、发电机和叶片等[5]。对长期运行风电机组的相关故障统计资料分析可知，就风电机组而言，传动系统的故障主要集中在轴承和齿轮箱，且故障发生率极高，机组齿轮箱损坏率达40%～50%[6]，故本文选取传动系统的齿轮箱为主要诊断对象。而近几年出现的果蝇算法目前在国外被广泛地用于算法模型优化，具有实用价值。因此，本文采用果蝇算法优化BP神经网络，得出风电机组齿轮箱故障诊断新方法。

1 风电机组齿轮箱故障诊断

风电机组长期处于微小震动作用中，风机表面在常期工作的情况下会产生微小磨损，引起表面划伤、咬死等现象；齿轮箱容易发生断齿、齿面疲劳、胶合等故障[7-8]。在风电机组的故障诊断中，常通过采集齿轮箱振动信号、扭矩、润滑油（油压、油温、杂质）等来监测其运行状态，并通过时域、频域、时频域分析提取故障特征[8]，为后续的故障诊断、分类提供信息基础。

目前，国内外故障诊断的研究方法主要包括[9-10]：

1）基于模型的诊断方法，即通过已有的理论建立相应的模型来反映系统或组件相关的物理或过程变化。

2）基于人工智能的方法，如通过神经网络方法，依靠其极强的非线性拟合能力、非局限性和非定常性，对故障进行分类，实现模式识别。

本文在人工智能方法的基础上，基于果蝇算法对神经网络进行改进，对齿轮箱进行故障诊断，得出故障分类。结果表明，基于果蝇算法优化的BP神经网络对风电机组齿轮箱故障具有较好的诊断效果[11-14]。

2 果蝇算法优化BP神经网络

2.1 BP神经网络

BP神经网络是一种采用误差反向传播的多层前馈神经网络[15]。该网络在一般情况下分为3层：输入层、隐含层、输出层[16]。BP神经网络的训练是通过不停的调整神经网络中的权值和阈值来逼近所需的结果，最终使得输出误差达最小[17]。

BP网络的权系数调整规则为：

输出层权系数的调整

隐含层权系数的调整

对每一样本P的输入模式对的二次型准确函数为

则系统对N个样本的总准确函数为

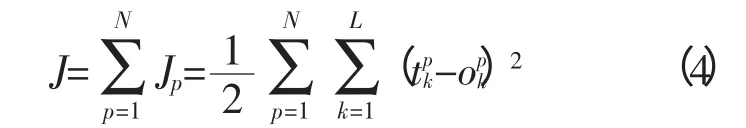
在众多的人工神经网络模型中，BP（ Back Propagation）网络更适合用于对复杂的机械设备进行故障诊断，在设备故障诊断领域中占有重要地位。BP网络的优点在于只要有足够的隐含层节点，网络可以逼近任意的非线性映射关系，而且BP网络这种全局逼近的办法，具有较好的泛化能力[18]。但BP神经网络也有不足之处，过多的隐含层节点在网络的训练过程中会不可避免地使训练时间加长，收敛速度变慢，且模型容易陷入局部最小，而不是全局最小。另外，BP网络的隐含层个数等参数都需要经验公式或人为调试，增大了网络学习负担。网络的学习也具有不稳定性，当新样本加入到训练中时，旧的样本有消失的趋势[19]。

2.2 果蝇算法

果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）是一种基于果蝇觅食行为推演出寻求全局优化的新方法，在粒子群等群智能算法的基础上发展而来[20]。果蝇优化算法为群智能的一种新方法，既属于演化式计算的范畴，亦属于人工智能的领域[21]。果蝇算法自2011年提出至今经历了4 a的发展期，目前在军事、工程、医学、管理与财务等领域得到了应用。其本身具有寻优速度快、不易陷入局部最优、稳定性高、寻优精度高等特点。

目前国外果蝇算法主要用来进行PID参数的整定，优化SVR进行船只经济型航行的预测，将果蝇优化算法（FOA）和遗传算法（GA）结合在一起进行多目标组合优化等。本文把果蝇算法应用于BP神经网络的训练中，可以有效地弥补BP神经网络容易陷入局部最优的缺陷，带来更精确的寻优结果。果蝇算法具体流程图如图1所示。

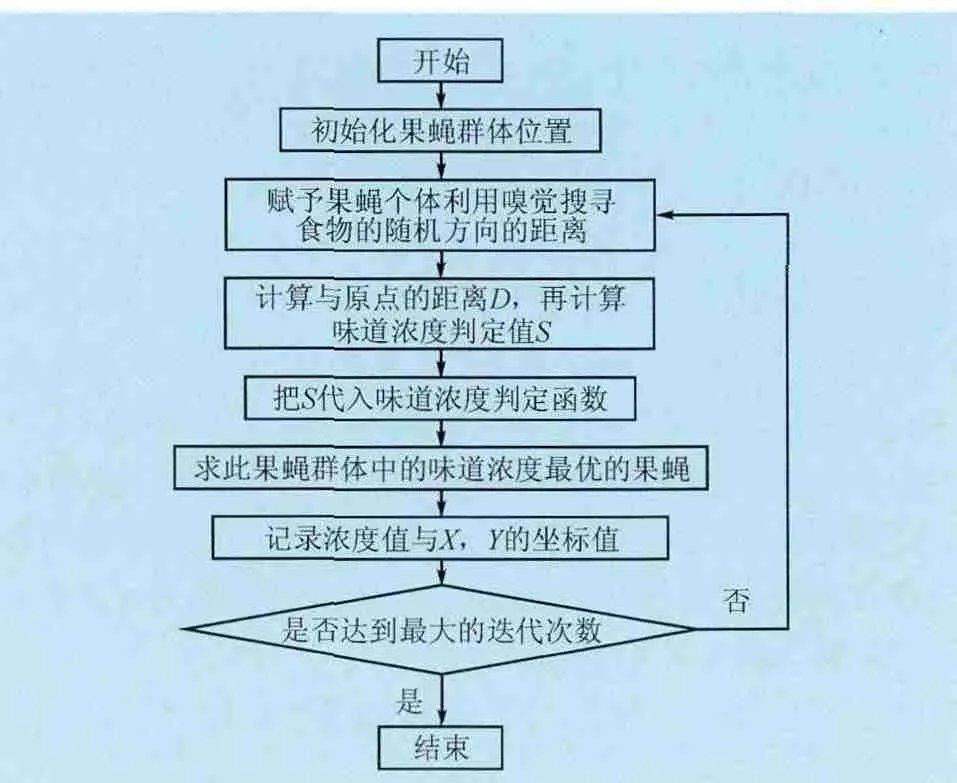
图1 果蝇算法流程图Fig. 1 Fruit Fly optimization algorithm flow chart

2.3 果蝇算法优化BP神经网络

采用果蝇算法优化BP神经网络，首先确定BP神经网络的结构。将BP神经网络中所有的权值和阈值视为果蝇个体，给每一组果蝇个体随机的方向和距离，按照算法步骤迭代，迭代过程中不停地寻找适应度函数的最优值，直到迭代完毕。

把优化后的权值和阈值带入BP神经网络，选取激活函数。确定以上内容后，带入训练数据，对BP神经网络进行训练。把测试数据带入训练好的BP神经网络进行测试。

本文使用果蝇算法优化神经网络的步骤如下：

1）初始化BP神经网络，确定BP神经网络每层中神经元的个数，确定输入层、隐含层、输出层的神经元的个数。每层的个数确定后就可以算出权值和阈值的具体数目。

2）把所有权值和阈值当做果蝇个体，初始化它们的位置，即

3）赋予每个权值和阈值搜寻全局最优值的随机方向和距离，即

式中，XF、YF、m分别表示随机的方向和距离。

4）由于无法得知最优值，所以先估计与原点的距离（Distance），再计算味道浓度判定值（S），此值为距离的倒数，即

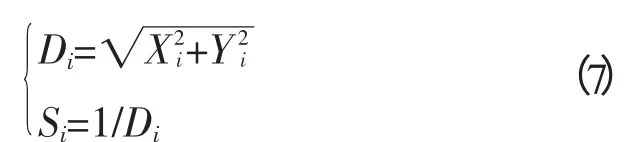
5）把4）中的S带入适应度函数中，此值作为判定值，并记录下来，即

6）求出神经网络适应度函数的最优值，这里显然要取最小值，并记录下此时的权值、阈值，即

7）更新最优适应度函数的值与权值和阈值的坐标，即

8）重复执行3）～6），并判断适应度函数的值是否优于前一代的值，若是则执行7）。

9）把求得的最优的权值与阈值带入BP神经网络用于训练。

10）把测试数据带入训练好的BP神经网络进行验证。

3 FOA-BP神经网络仿真分析

3.1 数据处理

本文所用数据为国产某1.5 MW机组的齿轮箱数据，该数据采集了齿轮箱的振动信号。样本大小为8 936，采样频率为5 120 Hz。由于采集环境的复杂性，机组运行的不稳定性，使得采集上来的振动信号无法直接用来训练，需要进行消除多项式趋势项和数据平滑处理。

3.1.1 消除多项式趋势项

在采集振动信号数据时，由于环境等因素使得采集上来的数据部分偏离基线。偏离基线随时间变化的整个过程称为信号的趋势项。趋势项直接影响信号的正确性，应消除。本文使用多项式最小二乘法消除趋势项。设采样数据为{xi}（k=1，2，3，…，n），把采样数据拟合成一个多项式，然后用样本数据减去拟合函数的数据，即

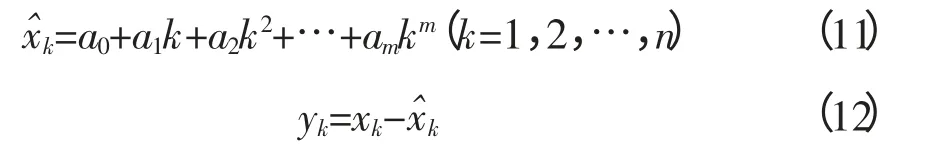
3.1.2 数据的平滑处理

采集得到的振动信号往往叠加有噪声信号。为了削弱干扰信号的影响，提高振动曲线光滑度，常常要对采样数据进行平滑处理。数据的平滑处理可以消除信号的不规则趋势项。本文采用五点三次平滑法进行平滑处理。五点三次平滑法计算公式如下：

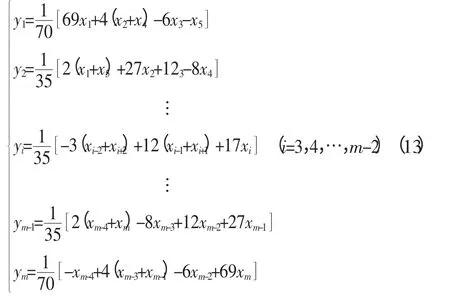
3.2 特征向量的提取

由于风电机组运行不稳定，所以齿轮箱轴承磨损比较普遍，其中震动信号的频率非常丰富。由于故障的发生会引起频带能量的变化，所以本文使用每个频带的能量作为信号的特征向量，频带能量的特征向量可以由小波包分解得到。本文采用了sym8小波对数据处理后的震动信号进行了3层分解消噪，然后采用了db1小波对处理后的振动信号进行3层小波包分解，分解后可以得到每个时刻的特征向量，最后建立特征向量与轴承状态的故障模型。样本信号中所含的齿轮箱故障包括轴承的滚动体故障、轴承内圈故障、轴承外圈故障。每种故障状态取13组进行算例分析。其中10组作为训练样本，另外3组作为测试样本。3层小波包分解后的部分训练样本的特征向量如表1所示。

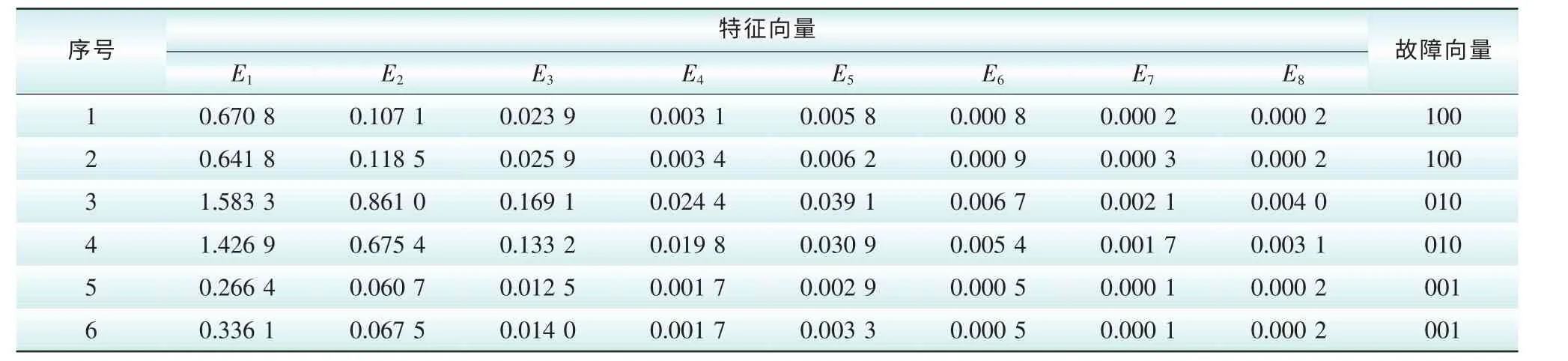
表1 部分特征向量Tab. 1 Part of the feature vector

表1中原始的振动信号为x（t），最高频率成分为f，最低的频率成分为0f[22]。利用小波包法把震动信号平分成的8个频带为0f～0.125f、0.125f～0.250f、0.250f～0.375f、0.375f～0.500f、0.500f～0.625f、0.625f～0.750f、0.750f～0.875f、0.875f～f。为了方便分析计算，对特征向量进行归一化处理。最后得到归一化后的特征向量是

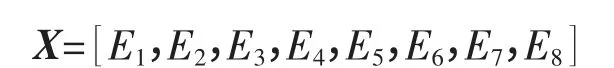
3.3 FOA-BP模型各项参数设置

本文建立了一个3层的BP神经网络，首先根据齿轮箱故障特征向量确定BP神经网络的输入层节点数为8，输出层节点数为3，隐含层节点则需要进一步确定。本文所用BP网络隐含层激活函数为Sigmoid型正切函数tansig，输出层传递函数采用Sigmoid型纯线性函数purelin，训练函数为trainlm，网络的训练次数为1 000，训练目标的误差为0.000 1，学习效率为0.1。

图2是不同隐含层节点数下神经网络的误差值，由于隐含层的节点数对神经网络起着重要的作用，过少拟合数据时偏差大，过多就会产生数据的过拟合，网络的泛化能力随之下降。在实际选取隐含层节点数时，本文将隐含层节点数暂定为10，逐步增加到20，在这个累加的过程中寻找最佳的隐含层节点数。由图2可知隐含层节点数选取15时，网络的误差最小。

其次，进一步确定果蝇算法的果蝇群体数为30，迭代次数为100。本文应用理想输出矩阵与测试数据的输出矩阵的差的二范数作为果蝇算法的适应度函数，即

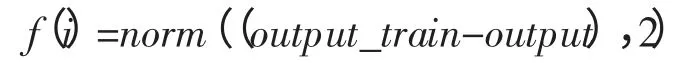
式中，norm为求二范数的函数；output_train为训练用的理想输出矩阵了；output为训练过程中BP神经网络的输出矩阵。

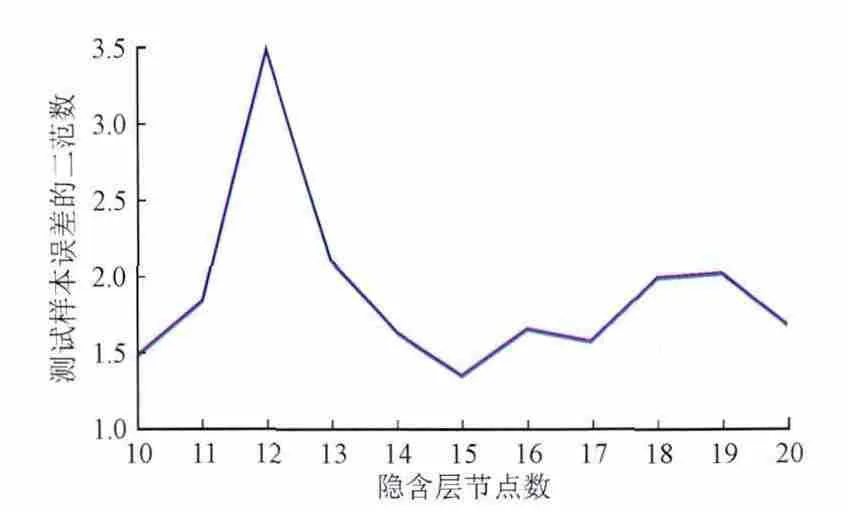
图2 不同隐含层的神经网络的误差Fig. 2 The error of the different hidden layer of neural network

4 结果与分析

图3是用果蝇算法优化BP神经网络的优化路径，由曲线可看出，果蝇算法优化到20多代时算法达到局部最优，当到达67代时逃离局部最优，第70代后，适应度函数达到了最优，此时适应度函数值为0.283 2。然后将果蝇算法寻得的最优权值和阈值带入到BP神经网络中，输入训练数据，得到优化后的BP神经网络。

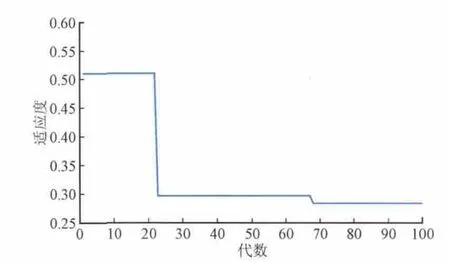
图3 果蝇算法寻优过程Fig. 3 FOA optimization process

本文分别选用BP神经网络和果蝇算法优化后的BP神经网络对齿轮箱故障数据进行训练测试，得出对比图（图4是BP神经网络的训练曲线；图5是果蝇算法优化后的BP神经网络的训练曲线）。

由图4、图5可得，BP神经网络经过58代的训练达到期望误差，经果蝇算法优化后的BP神经网络经过10代的训练即可达到期望误差。对比图4、图5可知，经果蝇算法优化后的BP神经网络可以迅速的达到期望误差，显著地加快了训练速度。

表2是2种诊断方法的测试结果的对比数据，由于每次训练得出的BP神经网络的内部结构都不一致，本文对2种方法分别进行10次训练和测试，选取最好的一组测试结果进行对比分析。

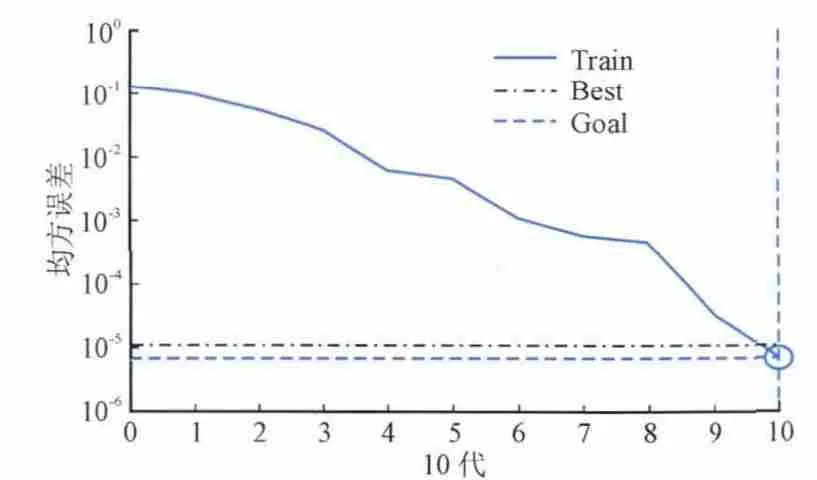
图5 FOA-BP训练曲线Fig. 5 FOA-BP performance curve

表2 测试结果的对比Tab. 2 Comparison of test results

设故障诊断原则为：大于等于0.5为1，小于0.5为0，所得测试结果应尽可能接近1或0。由表2可以看出BP神经网络所测试的第4组数据出现了错误诊断故障类型的情况，第5组、第8组的输出结果偏离1、0比较大，尤其是第5组数据已经非常接近0.5的限值，不能达到训练输出尽可能接近0或1的要求。而由果蝇算法优化后的BP神经网络的输出则总体令人满意，实际输出和期望输出相差无几，精度远高于果蝇算法优化前的BP神经网络。统计结果表明：在风机故障模型中，果蝇算法优化后的BP神经网络故障诊断的准确性优于BP神经网络。

5 结语

本文提出了一种基于果蝇算法对BP神经网络进行优化的方法，将果蝇算法与BP神经网络进行了结合，利用果蝇算法的全局搜索能力，防止BP神经网络在训练中陷入局部最优。对BP神经网络的网络结构进行优化，减小了训练时间，提高了训练效率。将该方法应用到了风机齿轮箱的故障诊断中去，结合试验数据对其进行了验证。验证结果表明，由果蝇算法优化后的BP神经网络的模型比BP神经网络的模型具有更高的准确性和快速性，而且精度更高，能够有效的对风机故障类型进行诊断。

[1] 赵稼祥. 复合材料在风力发电上的应用[J]. 高科技纤维与应用，2003，4（5）：43-47.ZHAO Jiaxiang. The application of composites in wind power[J]. High-tech Fibers and Applications，2003，4（5）：43-47（in Chinese）.

[2] 李春曦，王佳，叶学民，等. 我国新能源发展现状及前景[J]. 电力科学与工程，2012，28（4）：2-3.LI Chunxi，WANG Jia，YE Xuemin，et al. Industrial economic development is closely related to energy[J]. Electric Power Science and Engineering，2012，28（4）: 2-3（in Chinese）.

[3] 矜岳亮. 风电机组发电机的技术发展和展望[J]. 电力与能源，2011，32（4）: 325-327.JIN Yueliang. Technological developments and prospects of wind turbine generators[J]. Power and Energy，2011，32（4）: 325-327（in Chinese）.

[4] 白建华，辛颂旭，贾德香，等. 中国风电开发消纳及输送相关重大问题研究[J]. 电网与清洁能源，2010，26（1）：14-17.BAI Jianhua，XIN Songxu，JIA Dexiang，et al. Study of major questions of wind power digestion and transmission in Chinal[J]. Grid and Clean Energy，2010，26（1）：14-17（in Chinese）.

[5] 高洪慧. 基于LabVIEW和分形理论的风电机组故障诊断系统研究[D]. 北京：华北电力大学，2012.

[6] 麻东东. 风力发电机组远程状态监测与故障诊断系统的开发[D]. 保定：华北电力大学，2012.

[7] 孙自胜，樊炫君，谭涌波，等.基于一种智能型风力发电机浪涌保护器的设计与研究[J]. 电瓷避雷器，2014（1）：97-101.SUN Zisheng，FAN Xuanjun，TAN Yongbo. Research and design of an intelligent surge protective device for wind turbines[J]. Insulators and Surge Arresters，2014（1）：97-101（in Chinese）.

[8] 张晓杰. 齿轮箱中齿轮故障与振动分析[J]. 科技创新与应用，2013（28）：120.ZHANG Xiaojie. Gear in the gear box fault and vibration analysis[J]. Science and Technology Innovation and Application，2013（28）：120（in Chinese）.

[9] 李田田. 基于虚拟仪器的电路故障诊断[D]. 大连：大连理工大学，2007.

[10] 王斌. 面向风电机组齿轮箱的故障诊断系统研究[D]. 北京：华北电力大学，2012.

[11] 梁伟宸，许湘莲，庞可，等. 风电机组故障诊断实现方法探讨[J]. 高压电器，2011，8（47）：57-62.LIANG Weichen，XU Xianglian，PANG Ke，et al. Investigation of the implementation of the wind turbine fault diagnosis[J]. High Voltage Apparatus，2011，8（47）：57-62（in Chinese）.

[12] 徐跃进. 齿轮箱中齿轮故障的振动分析与诊断[J]. 机械设计，2009，26（12）：68-69.XU Yuejin. The vibration of the gear in the gear box fault analysis and diagnosis[J]. Mechanical Design，2009，26（12）：68-69（in Chinese）.

[13] 林近山，陈前. 基于非平稳时间序列双标度指数特征的齿轮箱故障诊断[J]. 机械工程学报，2012，13（2）：50-52.LIN Jinshan，CHEN Qian. Index based on non-stationary time series double scale characteristic of gearbox fault diagnosis[J]. Journal of Mechanical Engineering，2012，13（2）：50-52（in Chinese）.

[14] 窦春红. 基于LabVIEW的齿轮箱故障诊断系统设计[J].机械传动，2010，23（6）：31-33.DOU Chunhong. The gearbox fault diagnosis system based on labview design[J]. Mechanical Transmission，2010，23（6）：31-33（in Chinese）.

[15] 蒋良孝，李超群. 基于BP神经网络的函数逼近方法及其MATLAB实现[J]. 微型机与应用，2004，23（1）：52-53.JIANG Liangxiao，LI Chaoqun. The function approximation method based on BP neural network and MATLAB[J].Micro Computer and Application，2004，23（1）：52-53（in Chinese）.

[16] 马光志. 多代价敏感的反传神经网络优化研究[D]. 武汉：华中科技大学，2009.

[17] 李蓉. 神经网络在缺陷接地结构最优化设计中的应用研究[D]. 天津：天津大学，2007.

[18] 龙泉，刘永前，杨勇平. 基于粒子群优化BP神经网络的风电机组齿轮箱故障诊断方法[J]. 太阳能学报，2012，33（1）：120-125.LONG Quan，LIU Yongqian，YANG Yongping. The BP neural network based on particle swarm optimization method for wind turbine gearbox fault diagnosis[J]. Journal of Solar Energy，2012，33（1）：120-125（in Chinese）.

[19] 王景涛. 基于改进BP网络的多重分步损伤识别方法研究[D]. 北京：北京工业大学，2007.

[20] 韩俊英，刘成忠. 基于细菌趋化的果蝇优化算法[J]. 计算机应用，2013，33（4）：964-966.HAN Junying，LIU Chengzhong. Optimization algorithm based on bacterial chemotaxis flies[J]. Computer Application，2013，33（4）：964-966（in Chinese）.

[21] 王欣，杜康，秦斌，等. 基于果蝇优化算法的LSSVR干燥速率建模[J]. 控制工程，2012，19（4）：630-633.WANG Xin，DU Kang，QIN Bin，et al. The drying rate of LSSVR model based on fruit flies optimization algorithm[J].Control Engineering，2012，19（4）：630-633（in Chinese）.

[22] 施俊侠，杨兆建，张日红. 小波包分析方法在齿轮泵故障诊断中的应用[J]. 机床与液压，2010，38（17）：126－129.SHI Junxia，YANG Zhaojian，ZHANG Rihong. Wavelet packet analysis method in the application of the gear pump fault diagnosis[J]. Machine with Hydrau，2010，38（17）：126－129（in Chinese）.