中国西南地区栎类和桦木立木地上及地下生物量模型研建

甘世书，贺 鹏，肖前辉

(国家林业局中南林业调查规划设计院， 长沙 410014)

中国西南地区栎类和桦木立木地上及地下生物量模型研建

甘世书，贺 鹏，肖前辉

(国家林业局中南林业调查规划设计院， 长沙 410014)

依据中国西南地区栎类和桦木的立木材积及生物量实测数据，采用度量误差模型的方法，建立栎类和桦木材积相容的地上生物量及地下生物量模型。结果表明，在地上生物量模型中，增加树高因子，立木材积模型的相关统计指标有较大幅度的改进，栎类和桦木二元材积模型的平均预估精度分别达到了97.86%和97.08%，而二元地上生物量模型的相关统计指标并没明显的改进；两树种一元与二元地下生物量模型的相关统计指标差异并不明显，平均预估精度均达到了90%以上。

立木材积；地上生物量；地下生物量；度量误差模型；相容性7

前言

森林生态系统作为陆地生态系统的主体，在维持全球气候系统、调节全球碳平衡、减缓大气温室气体浓度上升等方面具有不可替代的作用。因此，世界各国越来越重视对大区域尺度的森林生物量的监测[1]。而建立各树种的生物量模型系统是生物量和碳储量监测、计量的重要基础工作。为开展全国森林生物量和碳汇监测和评估，建立合适较大区域范围的通用性立木生物量模型已成为必然趋势。

1 数据

1.1 数据来源

本次栎类和桦木的建模样本数据，于2012年6月至9月，在云南省和四川省境内采集，根据分布范围，按东、西、南、北、中均匀抽取，并且综合考虑立地条件、龄组结构等因素，确保所采集的样本具有充分的代表性。采集栎类样本量151株、桦木样本量150株。全部样本按照2，4，6，8，12，16，20，26，32，38 cm以上分10个径阶。每个径阶至少取15株样木，且每个径阶组内的样本量按3个树高级均匀分布。

对全部样本实测胸径和冠幅后，将样木伐倒，测量树干长度，分别测量0/10，0.5/10，1/10，2/10，3/10，4/10，5/10，6/10，7/10，8/10，9/10树高处的带皮和去皮直径及冠长，称取鲜质量；同时分别对干材、干皮、树枝、树叶进行采样，称其鲜质量，并取样带回实验室测定干质量，最后推算各部分干质量及地上部分总干质量(生物量)。其中约1/3的样本还同时测定地下生物量。

按公式(1)计算样木的带皮材积

(1)

1.2 异常数据处理

根据立木生物量建模样本采集技术规程的要求[3]，从建模样本数据库中提取以下核心信息：胸径、树高、带皮材积、干材生物量、干皮生物量、树枝生物量、树叶生物量、地上生物量、地下生物量和总生物量，单独形成文件；通过绘制胸径、树高与其他各因子的散点图，检查是否存在异常数据。经检查，栎类不存在异常样本，桦木删除5株异常样木。

经内业数据处理后的立木数据基本统计情况如表1。

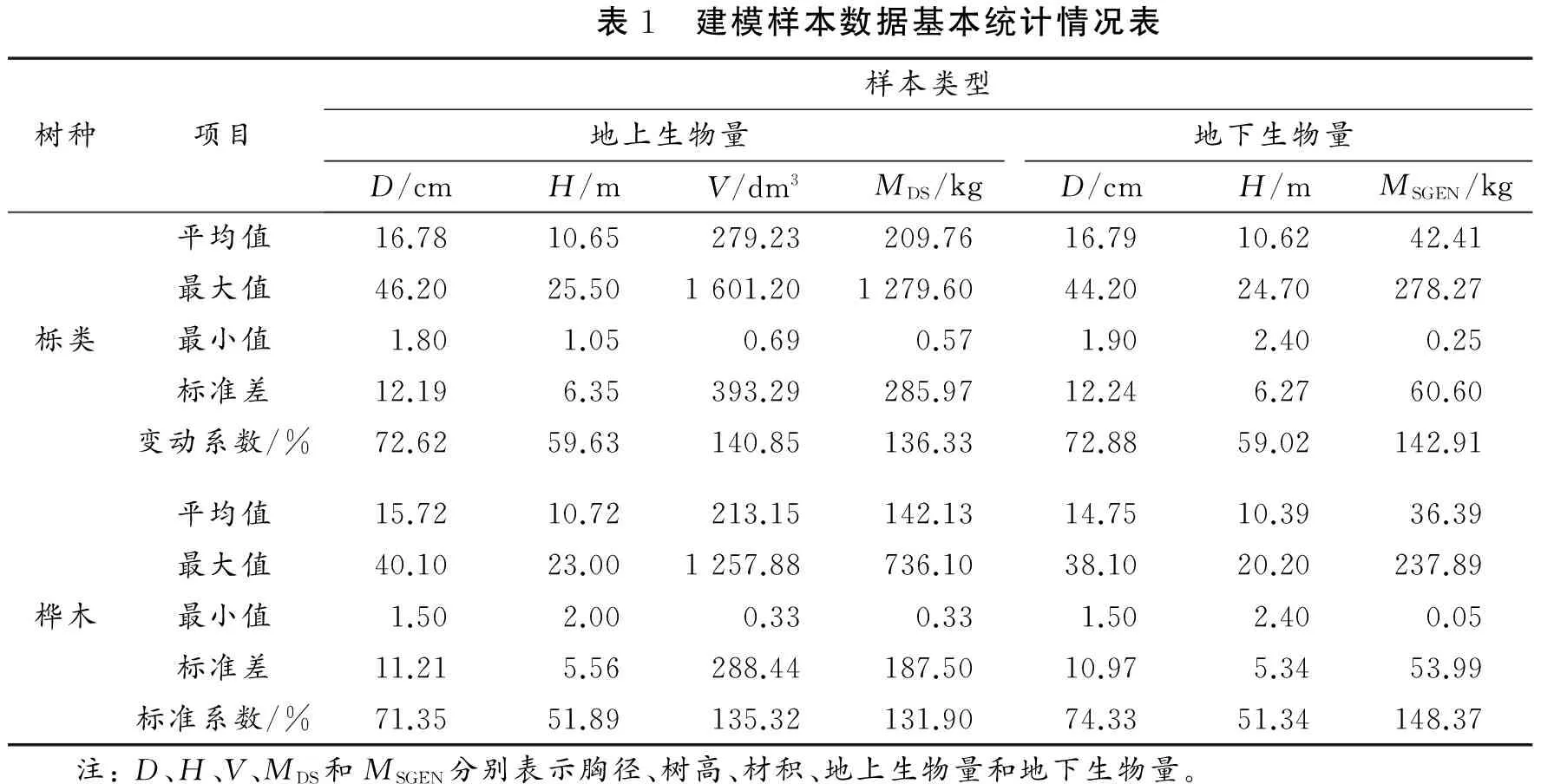
表1 建模样本数据基本统计情况表树种项目样本类型地上生物量地下生物量D/cmH/mV/dm3MDS/kgD/cmH/mMSGEN/kg平均值16.7810.65279.23209.7616.7910.6242.41最大值46.2025.501601.201279.6044.2024.70278.27栎类最小值1.801.050.690.571.902.400.25标准差12.196.35393.29285.9712.246.2760.60变动系数/%72.6259.63140.85136.3372.8859.02142.91平均值15.7210.72213.15142.1314.7510.3936.39最大值40.1023.001257.88736.1038.1020.20237.89桦木最小值1.502.000.330.331.502.400.05标准差11.215.56288.44187.5010.975.3453.99标准系数/%71.3551.89135.32131.9074.3351.34148.37 注:D、H、V、MDS和MSGEN分别表示胸径、树高、材积、地上生物量和地下生物量。

2 研究方法

2.1 度量误差模型

一般回归模型都假定模型中自变量的观测值不含误差，而因变量的观测值含有误差。而当自变量和因变量的观测值都含有度量误差时，通常的回归模型估计方法就不再适用了，而必需采用度量误差模型[4]，并同时对模型系统的参数同时进行估计。其模型的向量形式为：

(2)

式中：xi是q维无误差变量的观测数据，yi是p维误差变量的观测数据，f是m维向量函数，yi是Yi的未知真值，误差的协方差矩阵记为cov(ei)=σ2ψ，ψ是ei的误差结构矩阵，σ2为估计误差。

2.2 与材积相容的地上生物量模型系统

因地上生物量与立木材积高度相关，在森林蓄积监测的基础上进行森林生物量监测，应该充分考虑与材积的相容性，设计与材积相容的二元生物量模型如下：

V=a0Da1Ha2

(3)

M=b0Db1Hb2

(4)

M=f(D,H)V=c0Dc1Hc2V

(5)

式中：V为立木材积(dm3)；M为地上生物量(kg)；D为直径(cm)；H为树高(m)；f(D,H)相当于立木材积与地上生物量之间的转换函数(也可以称为生物量转换因子BCF)；aj，bj，cj为参数。

参数之间满足如下函数关系：

c0=b0/a0，c1=b1-a1，c2=b2-a2

(6)

如果分别独立拟合模型(3)，(4)和(5)式，则其参数不可能满足(6)式。因此，为了保证生物量M与材积V之间的相容性，可以将(3)和(5)两式构成非线性误差变量联立方程组，将D和H作为无误差变量，V和M作为误差变量，采用非线性度量误差模型的方法求解各个参数，保证以同一套数据为基础建立的立木材积模型和地上生物量模型是相容的，并同时得到满足相容性的立木材积与地上生物量之间转换函数。对于只考虑直径的一元模型也进行拟拟合，具体一元模型系统如下：

V=a0Da1

(7)

M=b0Db1

(8)

M=f(D,H)V=c0Dc1V

(9)

2.3 地下生物量模型(根茎比模型)研建

由于地下生物量测量难度比较大，实测样本数量相对较少。因此采用有限的实测地下生物量和地上生物量的样本建立相容的根茎比模型，与之前建立的与材积相容的地上生物量模型配合使用，模型结构如下：

一元模型：

M1=a0Da1

(10)

M2=RM1=c0Dc1M1

(11)

二元模型：

M1=a0Da1Ha2

(12)

M2=RM1=c0Dc1Hc2M1

(13)

式中M1和M2为实测的地下生物量和地上生物量；R为根茎比；D为直径；H为树高。采用非线性度量误差联立方程组进行参数估计。

2.4 异方差处理

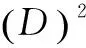
2.5 模型评价与检验

根据曾伟生[6]的研究结果，采用检验样本进行适用性检验的做法不可取，应该利用全部样本来建立模型，这样能够充分利用样本信息，使模型的预估误差最小。模型评价采用确定系数(R2)，估计值的标准差(SEE)，总相对误差(TRE)，平均系统误差(MSE)，平均预估误差(MPE)和平均百分标准误差(MPSE)6个指标，其详细计算公式参见文献[6]。

地下生物量模型的平均预估误差可根据地下生物量与地上生物量之间的相关系数，按(14)式计算：

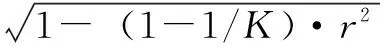
(14)

式中，K为测定地上生物量和地下生物量的样木数(视为一重样本与二重样本单元数)之比，r为相关系数，MPE2为利用二重样本建立的地下生物量模型估计值的误差，MPE1为综合一重样本后得到的地下生物量模型估计值的误差。

3 结果分析

3.1 与材积相容的地上生物量模型拟合结果

利用栎类和桦木全部建模样本的立木材积和地上生物量实测数据，采用度量误差模型方法，通过Forstat2.0软件进行参数求解，并利用参数估计值计算各相关统计指标。

表2，表3分别为栎类和桦木一元和二元立木材积模型，地上生物量模型以及转换函数的参数估计值和相关统计指标。结果表明：栎类和桦木一元材积模型的平均预估精度相近，均达到了94%以上，同时一元生物量模型的平均精度也均达到了93%以上。因此不管是一元材积模型还是一元生物量模型，模型的预估精度均较高。当模型从一元模型提高到二元模型时，栎类和桦木的立木材积模型的相关统计指标得到了较大幅度的改进，其中估计值的标准差SEE分别下降了58.1%和33.4%，平均预估误差MPE分别下降了近3个百分点和2个百分点，平均预估误差均控制在3%左右。但是栎类和桦木的二元地上生物量模型的相关统计指标的改进幅度的大小要小得多，其中估计值的标准差SEE分别下降了5.2%和2.5%，平均预估误差MPE分别下降了0.3个百分点和0.1个百分点。因此，立木材积二元模型较一元模型的预估精度有较大的改进，而地上生物量主要取决于胸径因子，二元地上生物量模型和一元地上生物量模型的差异不大。

3.2 地下生物量模型拟合结果

栎类和桦木根茎比模型的参数估计值以及相关的统计指标如表4。其中MPE2表示根茎比模型的平均预估误差，MPE1表示最终地下生物量模型的平均预估误差。结果表明，无论栎类还是桦木根茎比模型的平均预估误差均较大，接近20%。而根茎比模型通过与全部样本建立的地上生物量模型相结合而得到的新的地下生物量模型，精度明显提高，桦木在92%以上，栎类也超过了90%。

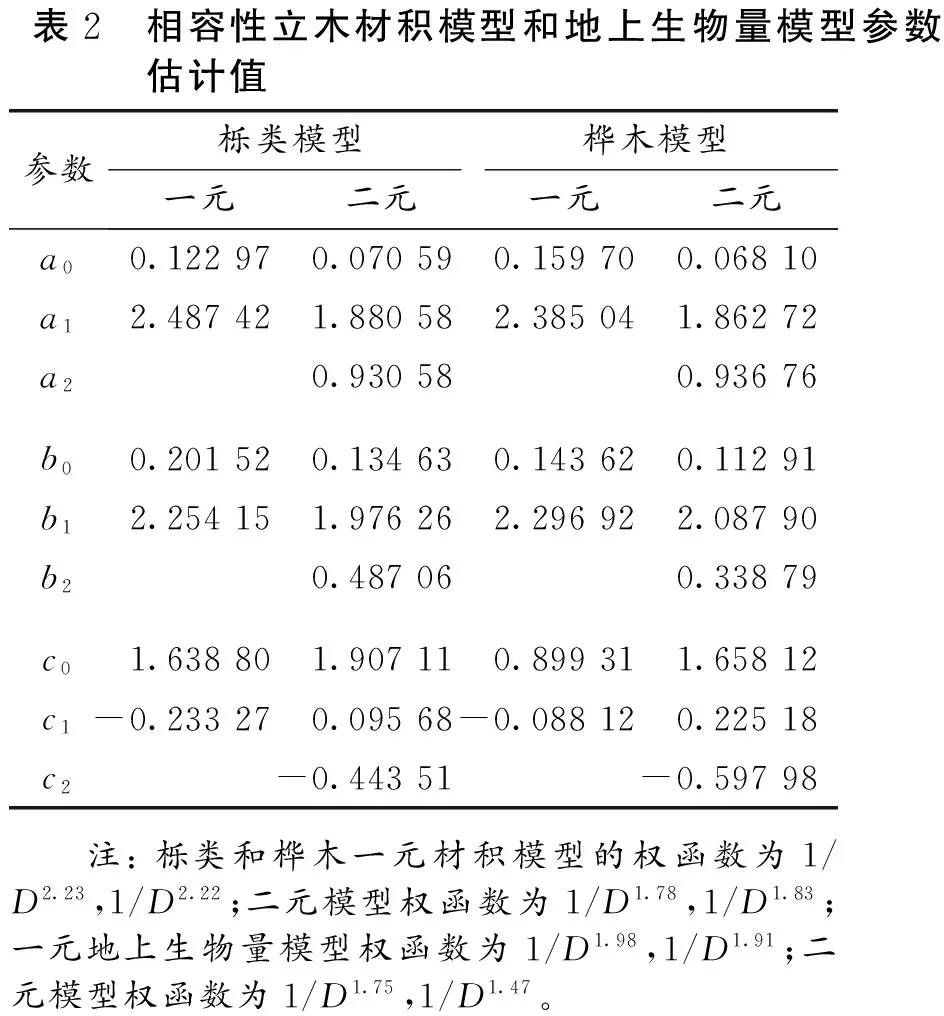
表2 相容性立木材积模型和地上生物量模型参数估计值参数栎类模型桦木模型一元二元一元二元a00.122970.070590.159700.06810a12.487421.880582.385041.86272a20.930580.93676b00.201520.134630.143620.11291b12.254151.976262.296922.08790b20.487060.33879c01.638801.907110.899311.65812c1-0.233270.09568-0.088120.22518c2-0.44351-0.59798 注:栎类和桦木一元材积模型的权函数为1/D2.23,1/D2.22;二元模型权函数为1/D1.78,1/D1.83;一元地上生物量模型权函数为1/D1.98,1/D1.91;二元模型权函数为1/D1.75,1/D1.47。

表3 相容性立木材积模型和地上生物量模型统计指标树种模型R2SEETRE/%MSE/%MPE/%MPSE/%材积生物量材积生物量材积生物量材积生物量材积生物量材积生物量栎类一元0.95000.912188.5785.330.632.380.681.605.116.5623.3831.14二元0.99120.921037.1480.900.470.513.866.752.146.2113.6631.32桦木一元0.93110.907076.2657.570.16-0.410.070.005.886.6623.1526.17二元0.96940.911550.8156.150.550.042.14-0.133.926.5013.1425.39

表4 根茎比模型参数估计值以及相关统计指标树种模型参数估计值相关统计指标abcR2SEETRE/%MSE/%MPE2/%MPSE/%MPE1/%栎类一元0.46926-0.239360.990229.564.551.6619.5241.549.28二元0.49390-0.17458-0.096210.990230.064.612.1319.8541.229.44桦木一元0.89931-0.088120.987823.110.09-0.1417.9753.747.16二元1.658120.22518-0.597980.988123.08-0.550.0917.9453.207.15 注:栎类和桦木一元地下生物量模型权函数为1/D1.81,1/D2.11;二元模型权函数为1/D1.82,1/D2.15;栎类和桦木一元地上生物量模型权函数为1/D1.66,1/D1.62;二元模型权函数为1/D1.69,1/D1.74。

4 结论

本文采用度量误差模型方法分别为中国西南地区栎类和桦木建立了立木生物量模型，包括与材积相容的地上生物量模型和地下生物量模型。可以得到以下结论:1) 无论是一元还是二元与材积的地上生物量模型系统，材积模型和地上生物量模型的预估精度较高，一元材积模型和地上生物量模型的预估精度均在94%和93%以上，二元材积模型和地上生物量模型的预估精度均在9 6%和93%以上。二元模型相对于一元模型而言，材积模型的预估精度改进的幅度较大，而地上生物量模型的预估精度并没有得到较明显的改进。

2) 通过二重样本地下生物量的实测数据建立根茎比模型，然后再与之前建立的地上生物模型配套使用得到地下生物量模型。这种双重估计的方法明显提高了地下生物量模型的预估精度。栎类一元和二元地下生物量模型的预估精度均在90%以上；桦木一元和二元地下生物量模型从模型的预估精度均在92%以上。两树种的一元模型和二元模型的之间的几乎没有差异。从模型的有效性和实用性角度考虑，建立一元地下生物量模型便可以满足实际需求。

[1] Tomppo E, Gschwantner T, Lawrence M, et al. NationalForest Inventories:Pathways for Common Reporting [M].NewYork:Springer,2010.

[2] 曾伟生, 肖前辉, 胡觉，等．中国南方马尾松立木生物量模型研建[J]. 中南林业科技大学学报, 2010, 30( 5) : 50- 55．

[3] 国家林业局森林资源管理司. 立木生物量建模样本采集技术规程[Z]. 2010．

[4] 唐守正, 郎奎建, 李海奎. 统计和生物数学模型计算： ForStat教程 [M]. 北京:科学出版社, 2009.

[5] 曾伟生, 骆期邦,贺东北. 论加权回归与建模[J]. 林业科学, 1999, 35(5): 5- 11.

[6] 曾伟生, 唐守正.立木生物量方程的优度评价和精度分析[J].林业科学, 2011, 47(11): 106-113.

EstablishmentofSingle-treeAbove-groundandBelow-groundBiomassModelsforQuercusandBirchintheSouthwesternChina

GAN Shishu，HE Peng，XIAO Qianhui

(Central South Forest Inventory and Planning Institute of State Forestry Administration， Changsha 410014，Hunan， China)

Based on the tree volume and above-ground biomass data of Quercus and Birch in southwestern China, single-tree biomass models systems of Quercus and Birch (including the compatible tree volume and above-ground biomass model and below-ground biomass model) were constructed by using the error-in-variable simultaneous equations. The results showed that:1) The regressions of volume equations improved significantly when tree height was used together with diameter at breast height (DBH), through the two variables-based equations, the prediction precision of tree volume of Quercus and Birch were 97.86% and 97.08% respectively, while the regressions of biomass equations improved slightly. 2) The difference was slightly small between one variable-based below-ground biomass model and two variables-based model. The prediction precision of below-ground model was more than 90%.

volume；above-ground biomass； below-ground biomass；error-variable-model；compatible model

2013-11-27

2014-03-04

甘世书(1963-)，男，湖南湘阴人，高级工程师，主要从事林业调查规划设计工作的。

S 718.55+6; S 758

A

1003-6075(2014)02-0001-04