液压作动器的全局滑模控制研究
孙 璐,郑春胜
SUN Lu, ZHENG Chun-sheng
(北京航天自动控制研究所,北京 100854)
0 引言
液压作动器具有高功率重量比、高刚度、高负载能力等优点,因而在机器人、大型机械设备、航空航天等领域得到了广泛应用。然而,液压作动器系统是一种典型的参数不确定非线性系统,其阀控动力机构流量非线性对系统性能影响较大,且时变、外负载干扰及非线性因素也导致了系统模型参数很大程度的不确定性。
由于液压作动器模型的非线性和参数不确定性,传统的PID控制算法已经很难满足液压作动器高精度、高速度的控制要求,各国学者针对液压作动器的特性也在不断研究新的控制策略和方法。模糊控制[1]和神经网络控制[2]已经在液压作动器的控制上得到了应用,但是他们在控制过程中,对外负载变化和扰动的抑制效果欠佳。滑模控制[3]是一种非线性控制方法,其对于系统不确定性及外扰动具有较强的自适应性,传统的滑模控制系统包括趋近模态和滑动模态,但系统在趋近模态时对系统参数摄动和外部干扰比较敏感,因此系统的动态性能和鲁棒性受到一定限制。针对传统滑模控制的不足,Lu[4]等提出了一种全局滑模控制器,设计新的滑模面来消除滑模控制趋近运动阶段,克服了系统非线性,时变等因素影响。

图1 液压作动器示意图
首先建立了液压作动器的数学模型,深入分析了模型的非线性特性及模型中各参数变化范围,在此基础上,推导了一种全局滑模控制算法,设计新的滑模面来消除滑模控制趋近运动阶段,很好的克服了系统非线性,时变等因素的不良影响,提高了液压作动器的控制性能。最后通过仿真实验验证了上述方法的正确性和有效性。
1 液压作动器建模
液压作动器由电液伺服阀和对称缸组成,液压作动器活塞连接负载,负载与环境的接触为弹簧阻尼模型,液压作动器工作原理[5]如图1所示。
整个液压作动器系统负载力平衡方程如下:

其中:x表示负载位移,m表示负载质量,A表示液压作动器腔体表面积,p1表示进油腔压强,p2表示回油腔压强,b表示负载与环境接触速度阻尼系数,k表示负载与环境接触弹性系数,F(t)表示外部干扰力与未建模摩擦力等。
根据液压作动器的流量连续方程:
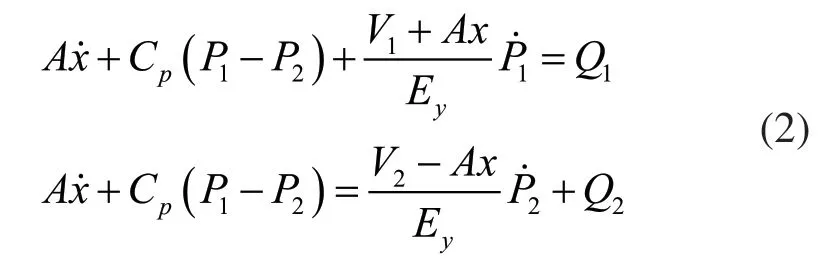
其中:V1表示初始时刻进油腔体积,V2表示初始时刻回油腔体积,Cp表示液压作动器内漏系数,Ey表示液压作动器等效容积弹性模数,Q1表示进油腔流量,Q2表示回油腔流量,分别为:
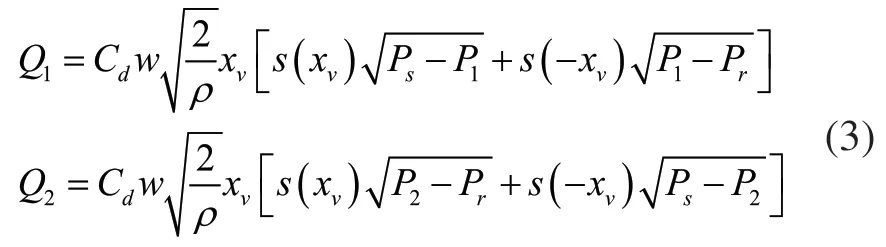
其中:Cd表示流量系数,w表示阀芯面积梯度,ρ 表示流体密度,xv表示阀位移,可用xv=λu表示[6],其中,u 表示控制量,λ表示放大系数。定义:
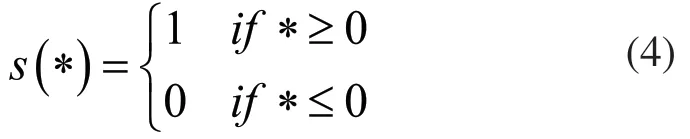
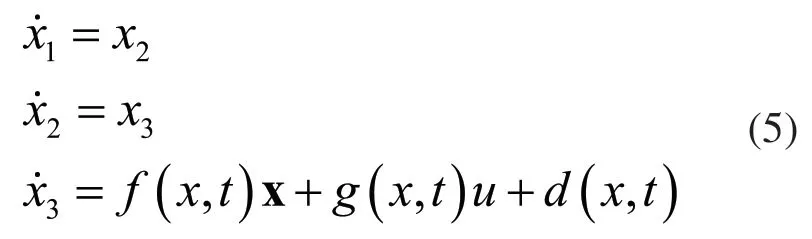
其中
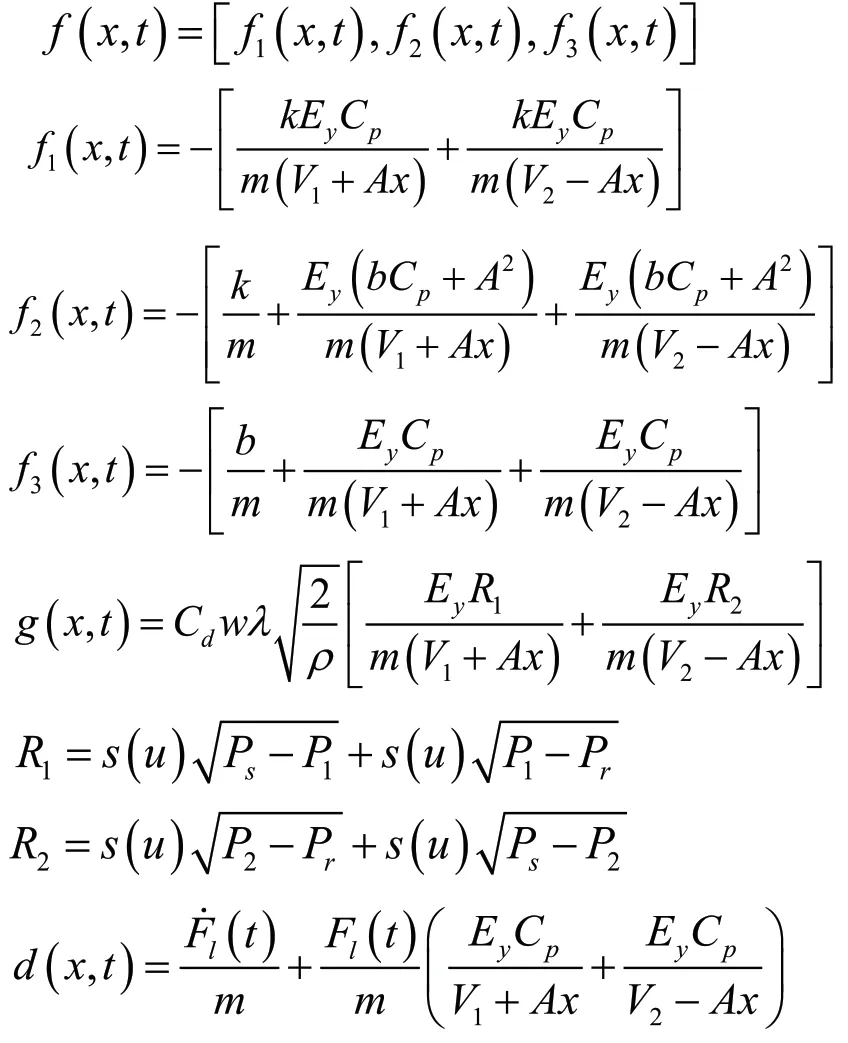
2 全局滑模控制器设计
从式(5)得到,液压作动器为一非线性系统,并且Ey,Cy和Cd参数由于不同的温度和环境,在系统运行整个过程中不断变化,w 和ρ也是不断变化的参数,由于运动过程中负载也可能不断变化,因此m,k和b也在不断变化。因此对于整个系统而言,其为一参数不确定的非线性系统。但是由于各参数均具有实际物理含义,在系统运行过程中,参数大小不存在突变情况,因此在实际物理系统中可作如下假设。
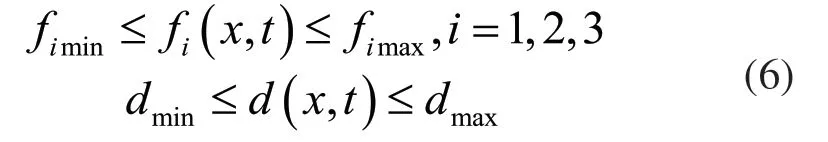
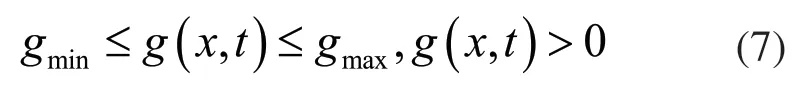

其中1c、c2均为正的常数。全局滑模控制的全局切换函数[7]与传统滑模控制切换函数的区别是式(8)右侧的全程滑态因子 w(t)必须满足以下三个条件:1);2)t →∞时,w(t )→∞;3)w(t)具有一阶导数。
根据以上三个条件,设计 w(t)为:
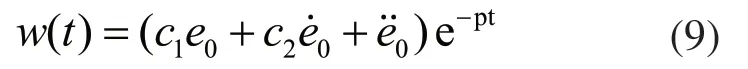

其中uc为等效控制,uvss为切换控制。
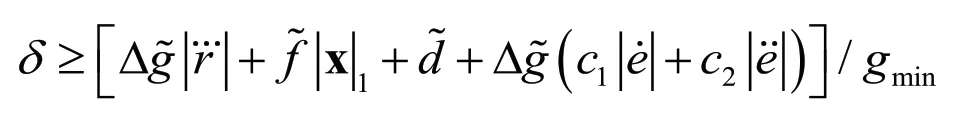
为了消除抖振,可采用饱和函数方法,即用sat(s)代替sgn(s)。
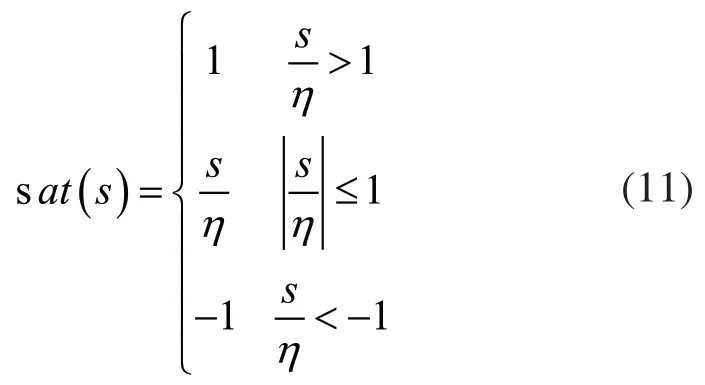
其中η为很小的正常数。
3 仿真分析
通过以上理论分析,采用全局滑模控制器进行液压作动器位置伺服控制仿真实验。控制频率设为1000Hz,为进行伺服阀过流保护,限制控制电压输入在-10V~+10V之间,进油压强30MPa,回油压强0MPa,环境刚度K为5000N/m,阻尼系数b为50Ns/m,Ey为700MPa,Cp为10-15(m3s/Pa),A为4.14×10-3m3,V1为2.1×10-4m3,V2为3.2×10-4m3,。
假设负载质量从100Kg变化到1000Kg,根据上述系统参数,设计控制器参数为:
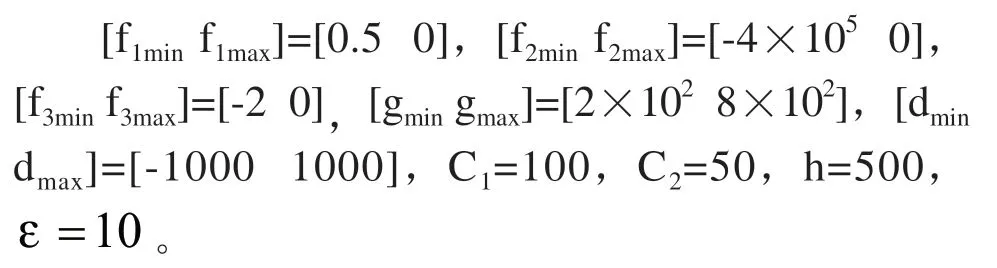
仿真分析中,采用正弦信号作为系统期望曲线,对比分析不同幅值、不同频率的期望信号输入时,不同负载情况下系统响应性能。进行了8组实验,分别是负载为100kg和1000kg时,系统对幅值为5mm、20mm,频率为0.6365Hz、2Hz的正弦信号跟踪情况,得到的实际位置曲线和期望位置曲线如图2~图9所示。

图2 0.6535Hz,1000kg,20mm

图3 2Hz,1000kg,20mm
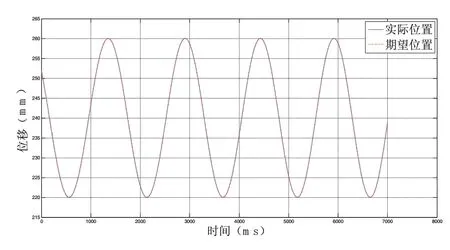
图4 0.6535Hz,100kg,20mm

图5 2Hz,100kg,20mm

图6 0.6535Hz,1000kg,5mm
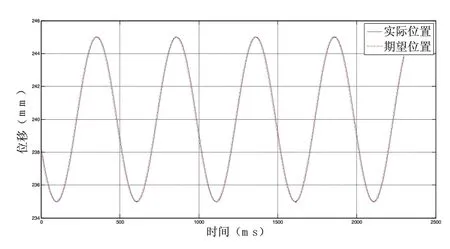
图7 2Hz,1000kg,5mm

图8 0.6535Hz,100kg,5mm
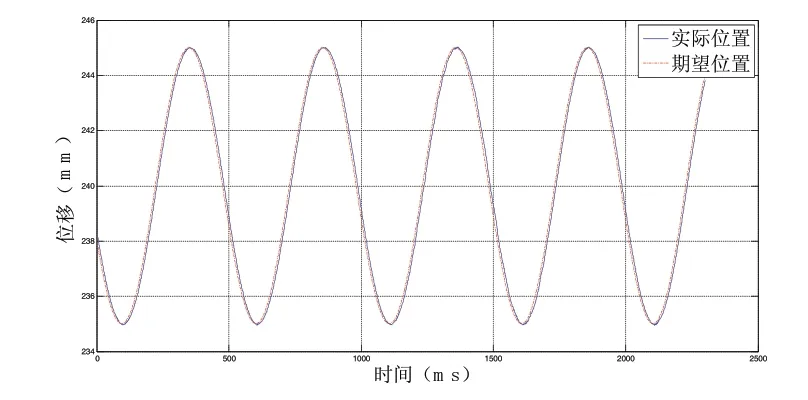
图9 2Hz,100kg,5mm
上述图中,横轴代表采样时间,单位ms,纵轴代表液压作动器长度,单位mm。对比分析图2、图4,图6、图8,当输入信号频率为0.6535Hz,幅值分别为5mm、20mm时,将负载由100kg变化到1000kg,液压作动器都能较好的跟踪输入期望信号,时延为5ms,跟踪误差为10-2量级,可见运用上述的全局滑模控制算法,使液压作动器位置伺服系统在整个响应阶段有较好的动态性能,且有较好的负载匹配能力和抑制干扰能力。
对比分析图3和图5,当输入信号频率为2Hz,幅值为20mm时,系统位置伺服跟踪存在较大时延和跟踪误差,这主要是由于液压作动器的控制量限定在[-10,+10]V之间,系统固有带宽限制了跟踪频率为2Hz,幅值为20mm的正弦信号作动器性能。对比分析图7、图9,当输入信号频率为2Hz,幅值为5mm时,将负载由100kg变化到1000kg,能得到较好的位置伺服效果。
4 结束语
由于全局滑模控制算法可以使得系统从任意初始状态就被约束在滑模面内,保证控制的全过程具有滑动模态特性,在建立了液压作动器动力学方程的基础上,设计了系统位置伺服的全局滑模控制器。仿真结果表明,全局滑模控制可以快速的实现全局滑动模态运动,具有很好的鲁棒性,可以匹配外界变化负载对系统位置伺服的影响,同时具有较高的控制精度和较好的动态特性。
[1]余兵,等.模糊控制及其在液压伺服系统中的应用[J].液压与气动,2006(10):56-64.
[2]陈平,等.液压伺服系统的直接自适应神经网络控制[J].机床与液压,2001(2):40-43.
[3]高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1996.
[4]Yu-Sheng Lu,Jian-Shiang Chen.Design of a global slidingmode controller for a motor drive with bounded control[J].International Journal of Control 62:5,1001-1019.
[5]Merritt.H.E.Hydraulic control systems[M].New York,Wiley,1967.
[6]王占林.近代电气液压伺服控制[M].北京:北京航空航天大学出版社,2005.
[7]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005.
[8]Cheng Guan,Shuangxia Pan.Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters[J].Control Engineering Practice,16(2008),1275-1284.

