非线性回归支持向量机的SMO算法改进

赵长春 姜晓爱

(北京航空航天大学 航空科学与工程学院，北京100191)

金英汉

(西北工业大学航天学院，西安710072)

支持向量机(SVM，Support Vector Machine)理论是Vapnik等人提出的一种新型的机器学习算法，在分类问题和回归问题上应用较广泛.由于SVM训练中需要求解二次规划问题，在训练大规模数据时占用内存空间较大，文献［1］提出了序列最小优化(SMO，Sequential Minimal Optimization)算法，该算法将问题分解为每次优化两个样本的Lagrange乘子，避免了求解二次规划问题，提高了训练速度.文献［2］详细介绍了SMO回归算法的实现方法，由于该算法训练时间较长，出现了许多对SMO算法的改进方法［3－5］，以缩短训练时间.此外，支持向量机的参数选择对训练模型的精度和训练速度影响较大，通过选择最优的支持向量机参数可以提高训练模型的准确度和训练效率［6－7］.参数优化方法的实质是利用测试样本对训练模型测试的精度来判断是否得到最优参数，参数寻优的过程就是不断改变参数值和用新参数反复训练模型的过程.因此，研究提高算法自身的训练速度的方法，能在很大程度缩短训练时间.

本文对SMO算法的改进方法进行了研究，提出新的改进算法用于非线性数据和非线性函数的回归，通过改进优化乘子更新方法、采用双阈值法、预存核函数、增加停机准则等方法加快了训练速度，提高了训练结果稳定性，最后对支持向量机参数选择方法做了讨论.

1 支持向量机回归

支持向量机回归的求解方法是将原始最小化问题转化为求其对偶最大化问题，对于样本集(xi，yi)，i=1，2，…，l，求解的对偶问题［2］可表示如下:

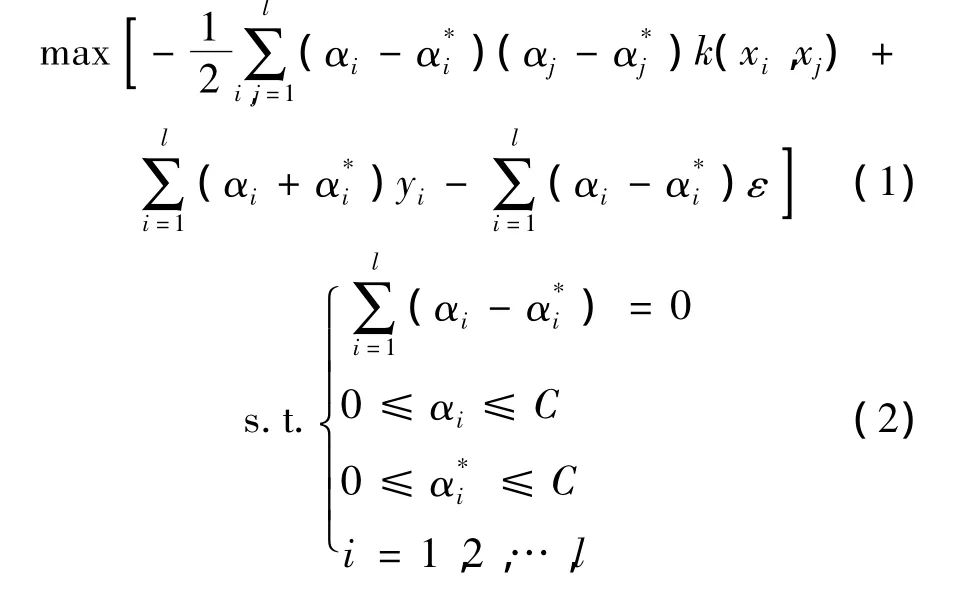
式中，ε为不敏感损失函数(示意图见图1);C为规则化参数，用于平衡回归函数的平坦程度;αi，为拉格朗日乘子;k(x，x)=Φ(x)·Φ(x)，ijij记为kij，为满足Mercer条件的核函数，Φ(·)为非线性映射.常用的核函数有线性核函数、多项式核函数、径向基核函数、Sigmoid核函数等.

回归函数可表示为

式中，b为阈值.

图1中，ε用于控制回归逼近误差范围，ξ≥0为松弛因子，表示回归函数值f(xi)与样本值yi之差的绝对值|f(xi)－yi|，当绝对值小于或等于ε时，取0，当绝对值大于ε时，取ξ.

图1 ε不敏感损失函数示意图

2 回归SMO算法理论

作变量代换，令

SMO算法每次只优化两个变量，固定其他变量值，设2 个待优化变量分别为，优化目标函数可表示成关于的函数:

式中，η=kuu－2kuv+kvv，当核函数满足 Mercer条件时，η≥0成立.

3 SMO算法改进

3.1 采用双阈值blow和bup

文献［3］中指出，由于阈值b正确性不确定，使得在优化中对已达到最优值的乘子更新，浪费执行时间，因此采用双阈值blow和bup的方法对算法做了改进.

令Fi=yi－〈ω，Φ(xi)〉，其中〈·，·〉表示内积，有以下5种情况:

根据式(9)和式(10)可定义b的上、下界，如下:

由于数值解原因，通常不可能获得准确的优化结果，因此，通过增加一项正误差τ获取近似优化结果，重新写式(12)，如下:

查找违反最优条件式(13)的样本作为待优化样本，即满足如下条件之一的样本为待优化样本:

3.2 优化乘子更新

由于Fu－Fv的值与b无关，通过其更新乘子可避免乘子优化结果受不准确的b值的影响，乘子更新步骤如下:

1)更新优化乘子分下面3个步骤.

①按如下式子进行更新:

②如果更新后两个乘子符号相同则得到本次更新结果，反之，定义调节变量Δ=2ε/η，如果根据Δ更新后的乘子和符号不改变，按式(16)进行:

③如果更新后的乘子符号发生改变，则设置乘子为0或sold，按如下条件进行:

2)约束优化乘子范围.

3.3 停机准则

目标问题与其对偶问题的对偶间隙为0时，达到全局最优解，但数值求解只能得到近似全局最优解，因此将对偶间隙作为停机准则，设定训练精度在达到预定值后停止计算［8－9］，减少训练时间.

定义如下关系:

记目标优化问题为函数 U(ω，ξ，ξ*)，对偶问题为函数W()，则函数表达式为

停机准则计算式为

当σ小于给定精度后停止训练，能缩短训练时间，将σ停机准则和式(14)的违反条件共同判断停止训练条件.

3.4 核函数矩阵计算和存储

在训练过程中，为避免重复计算核函数，训练开始时进行核函数矩阵存储.核函数矩阵是对称矩阵，存储时只需存储对称部分，假设有N个样本，则可用大小N(N+1)/2的一维数组aJ存储核函数矩阵，从主对角元素开始按主对角线方向顺序存储矩阵元素，如图2所示，元素kmn在矩阵中的位置与在数组aJ中位置对应关系如下:

式中，J为一维数组元素的下标;m，n分别为核函数矩阵元素kmn的行号和列号.核函数矩阵对称，只需计算主对角线和其上方的元素，其下方的元素与上方元素对称.规定m≤n，如果m＞n，交换m和n的值后再计算.

图2 核矩阵元素存储

3.5 改进的SMO算法描述

改进后的SMO算法具体步骤如下:

2)从整个样本中随机选择一个样本i，令blow=yi－ ε，bup=yi+ ε，ilow=i，iup=i.

3)SMO算法采用内、外两层循环选择待优化样本，步骤如下:

4)优化乘子更新步骤:采用3.2节乘子更新法更新优化样本的乘子.如果优化乘子的改变量大于一定值，则更新优化样本乘子和界内样本的误差值 Fi=yi－〈ω，Φ(xi)〉，并按式(11)在界内样本中寻找新的 blow，bup，ilow，iup.

5)在界内样本或所有样本遍历循环完成若干次迭代后计算一次停机准则σ值.

6)为防止优化程序出现死循环，当满足以下3个条件之一就结束算法:优化成功的样本数量为0、停机准则σ小于给定精度、迭代次数大于给定次数;如果没有满足条件的，则转3).

4 仿真实验及结果分析

将改进的算法与原始的SMO算法做对比，实验使用两个不同的拟合数据.通过对比达到相同停机准则时的时间和测试均方根误差(RMSE，Root Mean Square Error)来评价两个算法的优越性，RMSE表达式为

式中，N为测试样本总数;yi为样本目标值;为回归值.

4.1 仿真实验1

选取文献［10］中的训练样本作为算例，该数据具有非线性特点，样本如下:

所选择的测试样本如下:

选用径向基核函数，表达式如下:

参数设置基本原则:优化的参数对(C，γ2)的组合有很多［7］，样本数据变动趋势较平坦时，γ2取较大值，常取大于1的值;反之，取较小值，常取小于1的值;C值用于平衡回归函数平坦程度，一般取样本均值附近的值;ε控制回归函数逼近误差范围，根据实际需求取值;较小的τ值会增加训练时间，取值应当比ε取值小1～2个数量级;σ取值决定了训练精度，不宜过小，否则会增加训练时间.

根据上述基本原则和多次实验设置参数:C=4，γ2=2.1，ε =0.3，τ=0.000 1.采用在不同停机准则值下所用的训练时间和RMSE值作对比，表1为2种算法的对比.

表1 2种算法比较

从表1可以看出，与原始算法相比，改进后的算法训练时间明显缩短，但随着停机准则σ值减小而增加，因为停机准则σ值越小表示对偶间隙值越小，则训练时间会增加;2种算法的RMSE值随停机准则σ值减小而减小，在相同训练精度条件下，改进的算法能有效加快训练速度.

用改进的SMO算法训练非线性数据的回归结果如图3所示，从图中可看出，SMO算法对非线性数据拟合效果较好.

4.2 仿真实验2

选择函数进行拟合，函数表达式如下:

产生100个随机数点X，代入式(26)得到Y，组成训练样本(X，Y)，产生100个点随机数Xt，代入式(26)得到 Yt，组成测试样本(Xt，Yt).

图3 非线性数据回归结果(C=4，γ2=2.1)

选用径向基核函数，根据参数选择基本原则和多次实验设置参数:σ = －2，ε =0.01，τ =0.001.分别固定C值和固定γ2值，在这2种情况下对比2种算法的支持向量数目、训练时间、RMSE值.

从表2、表3可以看出，能得到较小RMSE值的最佳C值为1～1.5之间，最佳 γ2值为0.1;选取最佳 C和 γ2时，2种算法都能得到较小的RMSE值和较少的支持向量，较小的γ2值和较大的C值都会增加训练时间;与原始SMO算法相比，在达到相同的训练精度条件下，改进的算法明显缩短训练时间;原始算法使用了随机选择优化样本的方法，所以训练结果不稳定，同时也增加了训练时间，而改进后的算法使训练结果具有稳定性，使训练速度更快.

用改进的SMO算法对非线性函数回归的结果见图4，从图中可看出，SMO算法对非线性函数回归效果较好，随机测试样本测试误差较小.

表2 固定C=1.2情况下2种算法比较

表3 固定γ2=0.1情况下2种算法比较

图4 非线性函数回归结果(C=1.2，γ2=0.1)

5 结论

通过仿真实验，验证了支持向量机算法具有较强的非线性数据拟合功能，改进的SMO算法在训练速度和结果稳定性上得到提高.

实验表明，参数C和γ2，停机准则σ值对训练模型精度和训练速度影响较大，参数选择具有数据依赖性，仿真实验1中数据分布值域广，数据变化趋势较平坦，则γ2取较大值，仿真实验2中数据分布值域窄，数据变化较剧烈，则γ2取较小值，参数 C取值大致位于最大值和最小值的中间;停机准则σ值越小，训练时间越长，精度越高，可根据训练要求取不同值，如何更好地选择参数C和γ2是值得继续研究的方向.

References)

［1］ Platt J C.Fast training of support vector machines using sequential minimal optimization［R］.MSR-TR-98-14，1998

［2］ Smola A J，Scholkopf B.A tutorial on support vector regression［R］.NC2-TR-1998-030，1998

［3］ Shevade S K，Keerthi S S，Bhattacharyya C，et al.Improvements to SMO algorithm for SVM regression［J］.IEEE Transactions on Neural Networks，2000，11(5):1188 －1193

［4］ Flake G W，Lawrence S.Efficient SVM regression training with SMO［J］.Machine Learning，2002，46(1-3):271 －290

［5］ 张浩然，韩正之.回归支持向量机的改进序列最小优化学习算法［J］.软件学报，2003，14(12):2006 －2013 Zhang Haoran，Han Zhengzhi.An improved sequential minimal optimization learning algorithm for regression support vector machine［J］.Journal of Software，2003，14(12):2006 －2013(in Chinese)

［6］ 刘胜，李妍妍.自适应GA-SVM参数选择算法研究［J］.哈尔滨工程大学学报，2007，28(4):398 －402 Liu Sheng，Li Yanyan.Parameter selection algorithm for support Vector machines based on adaptive genetic algorithm ［J］.Journal of Harbin Engineering University，2007，28(4):398 － 402(in Chinese)

［7］ 闫国华，朱永生.支持向量机回归的参数选择方法［J］.计算机工程，2009，35(14):218 －220 Yan Guohua，Zhu Yongsheng.Parameters selection method for support vector machine regression ［J］.Computer Engineering，2009，35(14):218 －220(in Chinese)

［8］ 董磊，任章，李清东.基于SMO-SVR的飞机舵面损伤故障趋势预测 ［J］.北京航空航天大学学报，2012，38(10):1300－1305 Dong Lei，Ren Zhang，Li Qingdong.Fault prediction for aircraft control surface damage based on SMO-SVR ［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(10):1300－1305(in Chinese)

［9］ 王书舟，伞冶，张允昌.基于支持向量机改进 SMO算法的直升机旋翼自转着陆过程建模［J］.航空学报，2009，30(1):46－51 Wang Shuzhou，San Ye，Zhang Yunchang.Modeling for landing process of helicopter with rotator self-rotating based on modified SMO algorithm of support vector machine［J］.Acta Aeronautica et Astronautica Sinica，2009，30(1):46 －51(in Chinese)

［10］ 王定成.支持向量机建模预测与控制［M］.北京:气象出版社，2009:48－49 Wang Dingcheng.Prediction and control based on support vector machine modelling［M］.Beijing:Meteorological Press，2009:48－49(in Chinese)