基于PERT网络的航空弹药保障人员优化配置

郭小威 马登武 邓 力

(海军航空工程学院 兵器科学与技术系，烟台264001)

舰载航空弹药的保障工作主要由保障调度系统完成，各战位呈立体式分布且衔接紧密，保障工作实施难度大，高效、快速、可靠的弹药保障对舰载机的快速出动及再次出动能力影响重大.为此合理设计保障方案，并对相应的保障资源进行分配整合与优化十分必要［1－2］，为提高航空弹药保障的可靠性，在确定保障体系的情况下对保障人员进行合理优化配置的研究工作也势在必行.

在考虑任务风险、按期完工率和资源均衡等主要影响因素时，应用计划评审技术(PERT，Program Evaluation and Review Technique)对逻辑关系确定的保障流程进行分析较为适当.传统PERT网络分析方法以工作流程为基础，用各工序的期望持续时间和方差估计任务的完工概率［3－5］.以此为基础众多学者开展了关键路线和工序重要度及敏感性的研究工作［6－8］，大量仿真分析随计算机技术的发展也得以实现.蒙特卡罗(MC，Monte Carlo)方法引入到PERT网络的分析中，通过对PERT网络中关键路线/关键活动对任务工期的敏感性等的分析［9－12］，可以抓住重点对资源配置和工作进度进行有效控制［13－15］.而当前PERT网络在资源优化方面的分析多注重于有限资源下的工序按时开展与否，鲜少涉及通用资源的调整配置.鉴于此，本文通过分析每个保障人员配置方案中各工序对任务工期的影响程度，选取配置方案评价指标，进而优选出有限保障人员的配置方案.

1 基于MC法的PERT网络仿真

建立在MC法基础上的PERT网络仿真，其基本思想是由计算机模拟实际的工作实施概率过程，随机产生服从指定分布的工作时间，每一次仿真过程都产生一次各项工序的随机持续时间，各次过程下的工期和关键路线都可能不相同.经过多次的仿真统计分析，得到所需的各项工作指标数据，以此做出合理决策提高计划实施的可靠性.

1.1 PERT网络参数计算

PERT网络基于由n个节点组成的双代号网络图，(i－j)表示各项工序.

1.1.1 工序持续时间的概率特征

PERT网络中各项工序持续时间假设服从β分布，这也为多数文献所接受［16］.根据经典PERT的基本假设，在已知工序时间的最乐观值a、最可能值m和最悲观值b，采用式(1)确定工序持续时间的期望值μ和方差σ2:

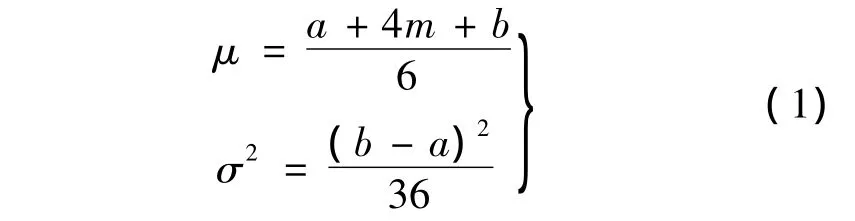
β分布的形状参数值γ和η由式(2)得出

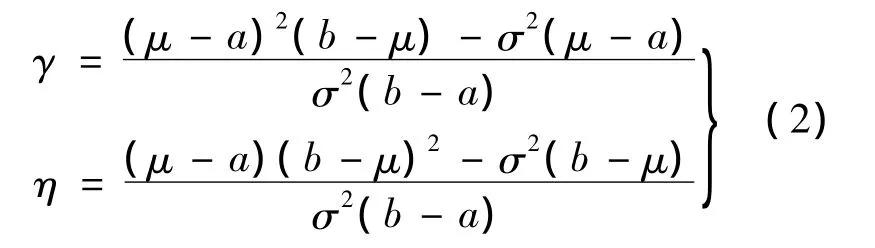
仿真过程中由上述参数组成各工序持续时间的随机数发生器.

1.1.2 按期完工概率

网络计划图中，各节点工序完成时刻的方差具有累加性.节点j的方差即是以j为终节点的关键路线上各工序持续时间的方差之和，表示为

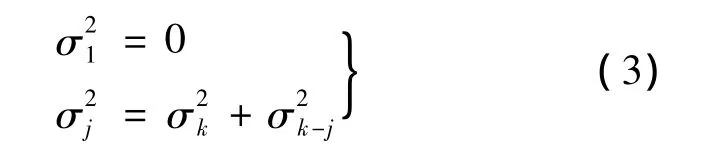
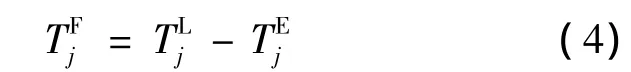
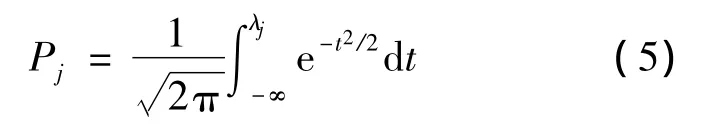
当节点j为网络图的结束节点n时，Pn就表示整个工程按期完工概率.

1.2 基于风险分析的关键指标

在工程网络计划中进行资源优化，往往需要考虑各工序相对重要程度以及对整个工程的影响程度.基于风险管理原则，引用工序关键度指标ACI(Activity Criticality Index)和工序重要度指标CRI(Cruciality Index)来分析各工序产生的影响.

关键路线上的关键工序直接决定了项目的完工期，而在PERT进度计划中，各工序持续时间的不确定性使得仿真过程中关键路线可能不唯一.最可能组成关键路线的各项工序就应予以重视.则工序的关键度指标定义为

式中mij为工序(i，j)在N次仿真中成为关键工序的次数，显然 p(i，j)∈［0，1］.

在进度计划中某工序的关键度大并不意味着该工序的风险量较大，也并不意味着整个工程项目不能完工的风险就大.因此，资源优化中除了需要考虑某工序成为关键工序的关键度外，还需要考虑其一旦发生意外时对整个工程项目进度的影响和进度的损失.可通过估计工作持续时间对项目工期的敏感度影响来评价，采用Williams提出的重要度指标CRI来表示，即

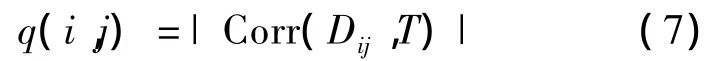
其数值可由以下各式求得

式中，Dij和分别为工序(i，j)的持续时间和第k次仿真时的持续时间;T和T(k)分别为工程总工期和第k次仿真时的总工期;E(Dij)和σ(Dij)分别为工序(i，j)的持续时间在N次仿真后的期望值和标准差;E(T)和σ(T)分别为N次仿真后工程总工期的期望值和标准差;Cov(Dij，T)和 Corr(Dij，T)分别为工序 (i，j)持续时间与总工期的协方差和线性相关系数.

2 保障人员优化配置建模

航空弹药保障具有批次量大、完成可靠性要求高的特点，要求合理配置所属保障人员以求保障效率最高.

2.1 问题分析

1)假设所配置的保障人员都能胜任所指定岗位的工作，亦即是保障工序持续时间参数只与保障人员数量有关.

2)整个保障流程的工序分为2部分:第1部分为基本由设施设备完成的工序，其持续时间的均值和方差固定;第2部分主要由保障人员完成，持续时间不确定，并且与保障人员数量有关.

3)第2部分各工序保障人员数量存在下限以保证工作的顺利完成，理论上讲人员数量越多工序持续时间越短，但由于组织协调、空间场地等的限制，工序持续时间只在一定范围内随人员数量变换，即需要设定各工序保障人员数量上限.

4)保障人员总数确定.

保障人员的优化配置即是在满足优化指标的情况下合理配置第2部分的保障人员.

2.2 优化配置模型

保障流程的PERT网络共计n个节点，共计na个工序，其中第2部分工序数量为nt，其保障人员数量的上下限标记为和某次人员配置方案为，则有…，nt)，并且要保证其第2部分保障人员数量总数一定，即为设定常数.在此方案下所有工序持续时间的期望值和方差分别为Dij(i，j∈{1，2，…，n})和 σij(i，j∈ {1，2，…，n})，第 1部分工序持续时间固定，而第2部分工序持续时间的期望值和方差则由保障人员的具体数量而定.

保障人员配置方案确定的情况下，亦即是各工序持续时间的期望值和方差得到确定，以此对PERT网络进行Monte Carlo仿真实验，以获取工程计划的所需数据.仿真次数设定为N，在计划工期Tp下第k次仿真获得的保障工作按期完工概率为，该方案下的工作按期完工概率取各次仿真结果的均值:

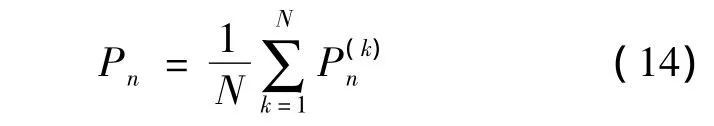
显然Pn越大保障工作按期完成的可能性越大，即是此配置方案更优.

另外，为使得整个保障工作中各工序实施紧凑，须保证各工序的总时差最小，也就是到达最终节点的各条路线的时长相差最小.反映在仿真过程中，就是每条路线都可能成为关键路线，即由式(6)计算得到的各工序关键度指标p(i，j)分布均衡，这里用标准差表示各工序关键度指标的离散度:

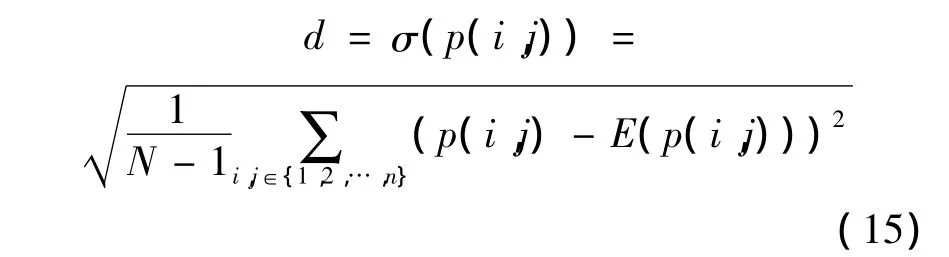
CRI反应了工序对任务工期的风险影响，为保证任务不受某些工序的较大影响，须使得各工序的CRI尽量均衡集中，同样用标准差表示CRI的离散度:

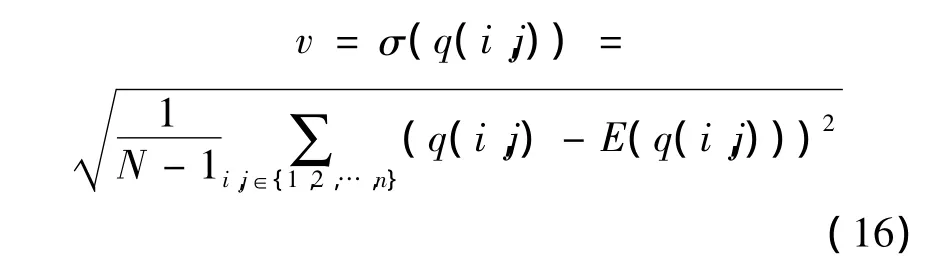
v值越小，表示工序CRI分布越集中，出现高风险工序的可能性越低.

根据式(14)～式(16)对保障人员配置方案优劣的影响，评价配置方案的函数表示为

2.3 工序均值和方差的确定

第2部分工序持续时间参数随保障人员的数量而变化，在其上下限范围内为便于计算，可认为其方差保持不变，期望值以工序保障人员数量上限为基础，按以下公式计算:

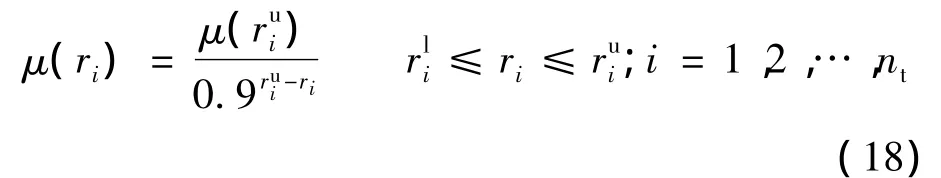
2.4 基于遗传算法的方案寻优

1)编码方案.遗传算法染色体采用实值编码方式.染色体共计nt个“基因”，顺次每个“基因”表示第2部分工序的保障人员数量，其数值大小在上下限范围之内.

2)适应度评估.寻求最优的保障人员配置方案即是解决目标函数(式(17))的最大化问题，又知f(R)＞0，则当∑R=NI时适应度函数可直接设为Fit［f(R)］=f(R)，否则采用惩罚策略降低该染色体的适应度值.

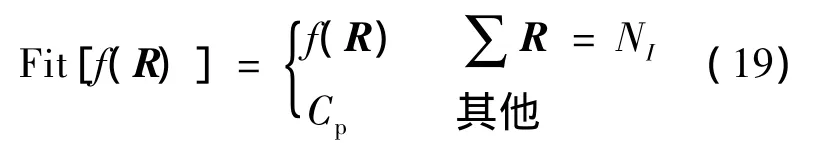
式中Cp是个极小值.

3)选择操作.根据每个染色体的适应度值大小采用轮盘赌选择策略实施.

4)交叉操作.采取两点交叉方式进行.

5)变异操作.在每个“基因”上下限范围内产生随机整数，取代原数值.

2.5 MC法仿真次数的确定

现代计算机性能的提高，也为大规模数据仿真的实现提供了可能，但由于每个配置方案都需要进行一次仿真，为实现算法的快速性有必要确定每次的仿真次数N.保障工作持续时间T服从分布，可由 1.1 节求得.为保证平均按期完工概率Pn真实反映保障工作持续时间，须使得N次仿真的均值趋近于其分布的期望值 μn，可表示为

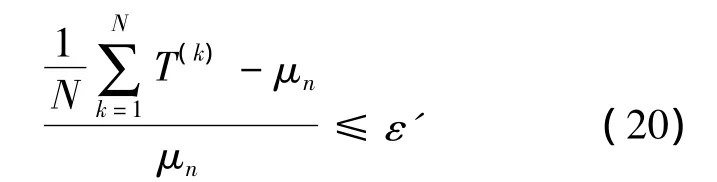
由辛钦大数定理可知［17］，对任意的 ε ＞0，有

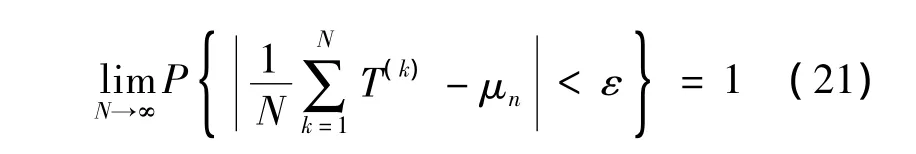
具体由Chebyshev不等式表示为

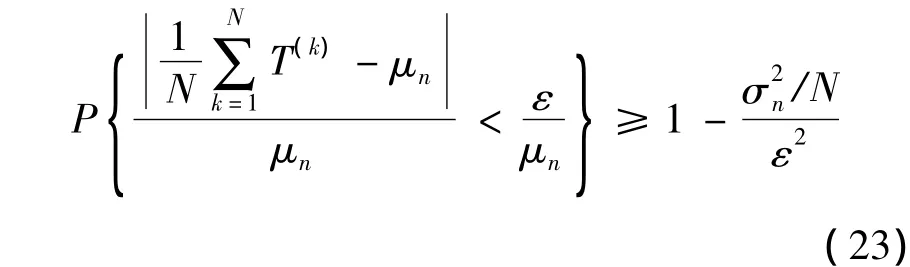
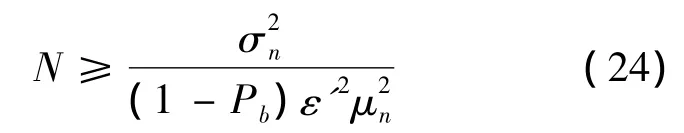
通过式(24)即可确定单个方案的仿真次数.

2.6 算法流程

以遗传算法为优选框架，基于Monte Carlo仿真方法的PERT网络求得优选指标，以此求解最优的航空弹药保障人员配置方案的流程如图1所示.

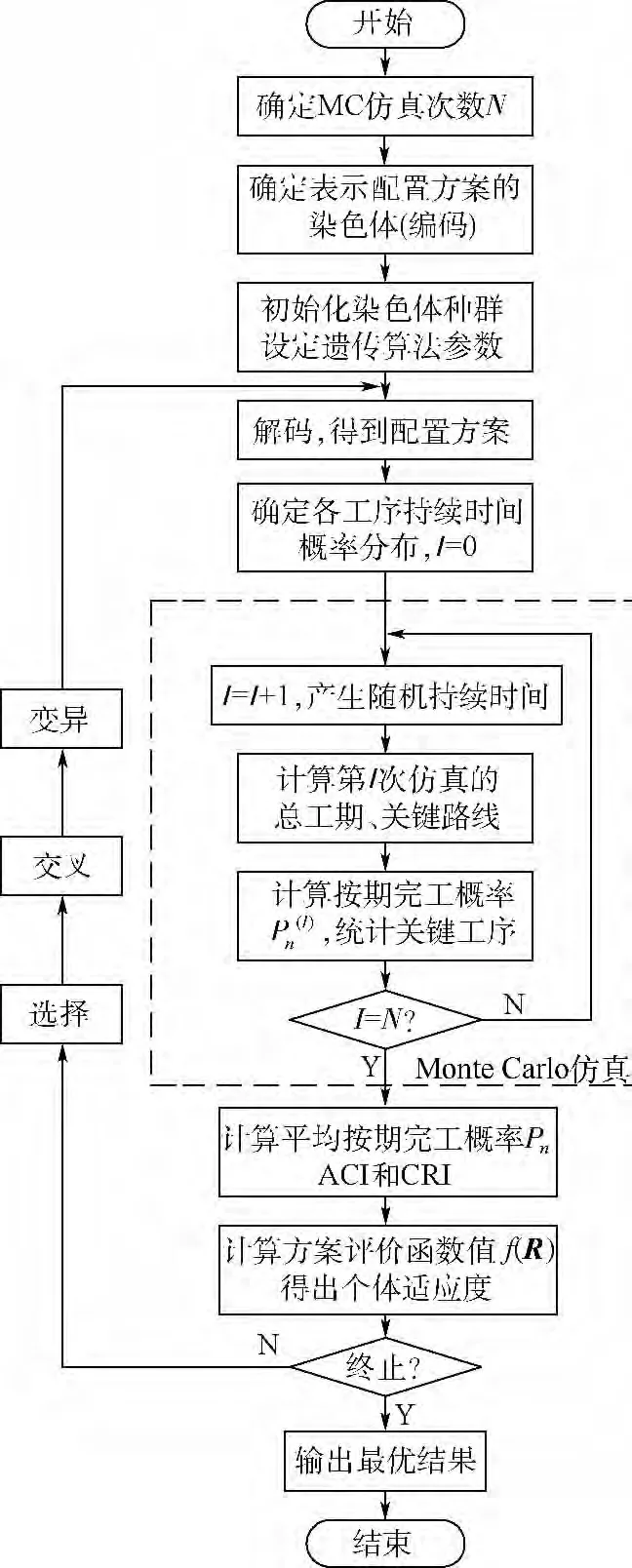
图1 算法流程图

3 算例分析

某次航空弹药保障任务的网络计划图如图2所示，其中虚箭线表示虚工序.工序箭线下方为工序保障人员数量上下限，上方为人员上限时的时间参数(单位为同一量纲)，Tp=550，保障人员总数100，可知第2部分工序保障人员数量NI=59.用各工序人员数量上限时的时间参数来估计Monte Carlo方法的仿真次数，此时的任务工期的均值与方差分别为 ¯μn=509.58 和 ¯σ2n=75.0 ，在参数 Pb=99.5% 和 ε′=1% 时 N≥577.7，这里取N=1000.

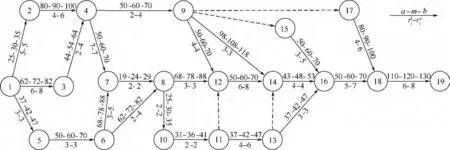
图2 PERT网络及工序参数表示

遗传算法参数设置为:进化代数100，染色体个数40，交叉概率 0.8，变异概率 0.1.权重系数ω =［0.6 0.2 0.2］时，以式(17)为目标函数采用所提出算法进行配置方案优选，进化曲线如图3所示，图中达到最优值时产生的微小波动由Monte Carlo仿真的随机性产生.

最终得到的最优方案及供需相关参数如表1所示，此方案的平均任务按期完工概率为99.61%.

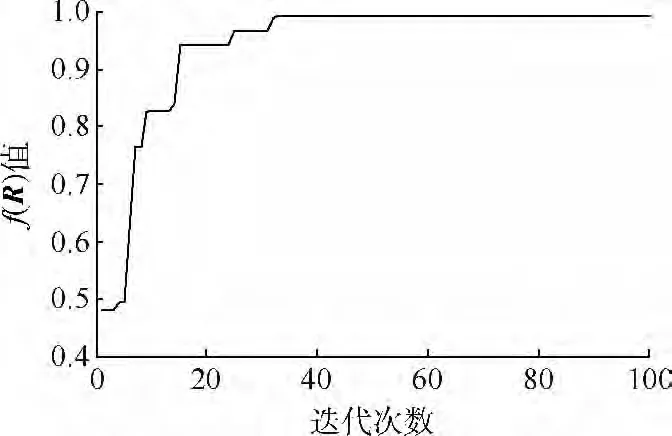
图3 目标函数进化曲线

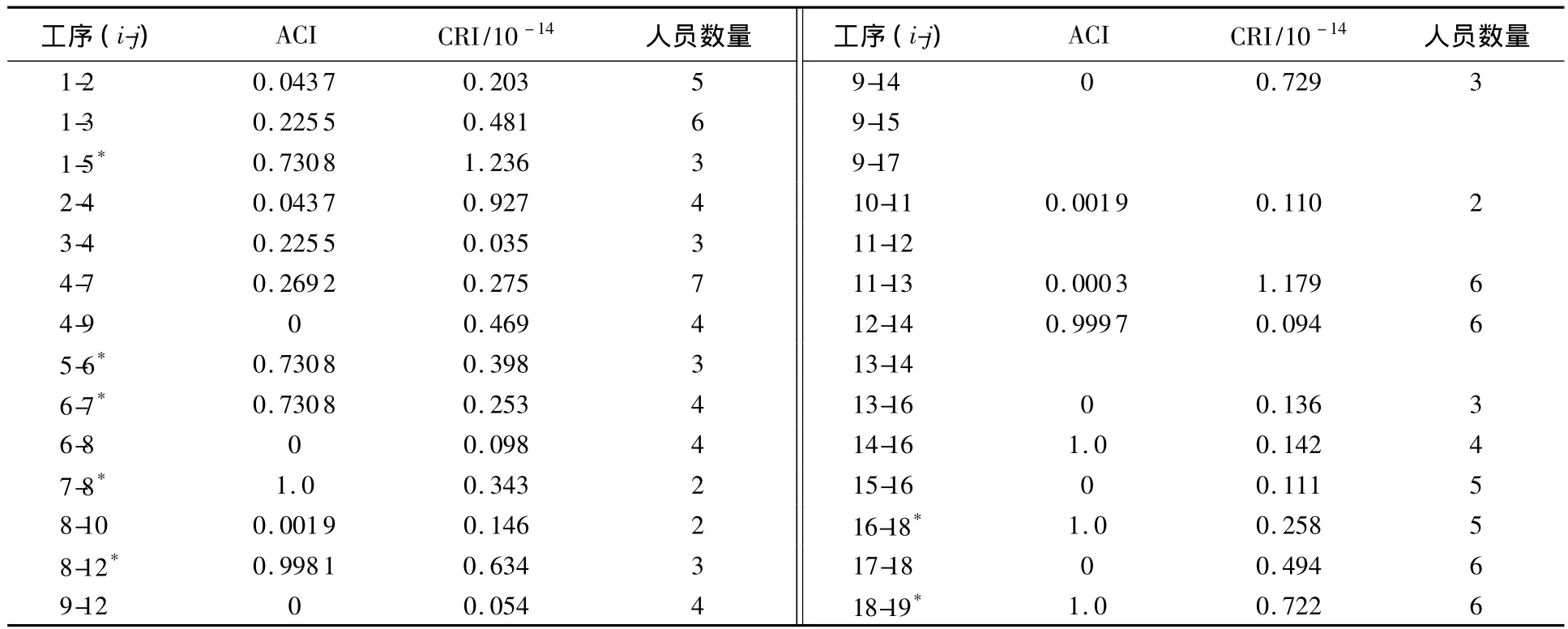
表1 优选配置方案工序参数

4 结论

航空弹药保障任务是一个复杂的系统工程，不仅要求按时按量高标准完成，又受到保障资源很大的制约，且任务工序充满着不确定性.合理科学地配置保障资源及控制计划进度直接影响到战机作战效率的高低.本文基于保障流程的不确定性，以PERT网络仿真为基础，在保证任务按期完工率的同时兼顾工期风险评价指标ACI和CRI，建立了人员配置方案寻优模型，对保障人员进行优化配置.有效保证保障工作的效率和均衡，以使弹药保障工作的高效稳定开展.以此为基础可进一步研究航空弹药多批次保障的资源优化问题.

References)

［1］马登武，郭小威，邓力.基于改进蚁群算法的舰载机弹药调度［J］.系统仿真学报，2012，24(6):1207 －1211 Ma Dengwu，Guo Xiaowei，Deng Li.Ammunition scheduling of carrier-based aircraft based on modified ant colony algorithm［J］.Journal of System Simulation，2012，24(6):1207 － 1211(in Chinese)

［2］马登武，郭小威，吕晓峰.基于网络计划技术的舰载机航空导弹转运流程［J］.兵工自动化，2010，29(9):48 －51 Ma Dengwu，Guo Xiaowei，Lü Xiaofeng.Airborne missile transport process of carrier-based aircraft based on network planning techniques［J］.Ordnance Industry Automation，2010，29(9):48－51(in Chinese)

［3］José Manuel Herrerías-Velasco，Rafael Herrerías-Pleguezuelo，Johan René van Dorp.Revisiting the PERT mean and variance［J］.European Journal of Operational Research，2011，210:448－451

［4］Castroa J，Gómeza D，Tejada J.A polynomial rule for the problem of sharing delay costs in PERT networks［J］.Computers ＆ Operations Research，2008，35:2376 －2387

［5］Premachandra I M.An approximation of the activity duration distribution in PERT［J］.Computers ＆ Operations Research，2001，28:443－452

［6］段建中，李民奎.PERT行为时间参数近似计算公式选优［J］.合肥工业大学学报:自然科学版，2001，24(3):365－369 Duan Jianzhong，Li Minkui.Optimizing estimation of PERT activity time parameters［J］.Journal of Hefei University of Technology:Natural Science，2001，24(3):365 －369(in Chinese)

［7］Fatemi G S M T，Teimouri E.Path critical index and activity critical index in PERT networks［J］.European Journal of Operational Research，2002，141(2):147 －152

［8］Cho J G，Yum B J.Functional estimation of activity criticality indices and sensitivity analysis of expected project completion time［J］.Journal of Operational Research Society，2004，55(8):850－859

［9］王卓甫，丁继勇，刘媛，等.基于Monte Carlo方法的PERT网络关键路线和最关键活动分析［J］.系统工程与电子技术，2012，34(8):1646 －1651 Wang Zhuofu，Ding Jiyong，Liu Yuan，et al.Analysis of critical path and most critical activity in PERT networks based on Monte Carlo method［J］.Systems Engineering and Electronics，2012，34(8):1646－1651(in Chinese)

［10］唐建，严骏，凌海风，等.基于随机PERT网络Monte-Carlo仿真的任务可靠性分析［J］.计算机应用研究，2012，29(8):2948－2951 Tang Jian，Yan Jun，Ling Haifeng，et al.Mission reliability analysis based on Monte-Carlo simulation of stochastic PERT network［J］.Application Research of Computers，2012，29(8):2948－2951(in Chinese)

［11］Baradaran S，Fatemi Ghomi S M T，Mobini M，et al.A hybrid scatter search approach for resource-constrained project scheduling problem in PERT-type networks［J］.Advances in Engineering Software，2010，41:966 －975

［12］Bowman R A.Efficient sensitivity analysis of PERT network performance measures to significant changes in activity time parameters［J］.Journal of Operational Research Society，2007，58(10):1354－1360

［13］Azaron A，Perkgoz C，Sakawa M.A genetic algorithm approach for the time-cost trade-off in PERT networks［J］.Applied Mathematics and Computation，2005，168:1317 －1339

［14］Azaron A，Tavakkoli-Moghaddam R.A multi-objective resource allocation problem in dynamic PERT networks［J］.Applied Mathematics and Computation，2006，181:163 －174

［15］Kong Xiangxing，Zhang Xuan，Hou Zhenting.Markov skeleton process in pert networks［J］.Acta Mathematica Scientia，2010，30B(5):1440 －1448

［16］李学京.置信分布的贝塔分布近似及其在可靠性统计中的应用［J］.强度与环境，2007，34(2):17－23 Li Xuejing.Beta distribution approximation of confidence distributions and application in reliability statistics［J］.Structure ＆Environment Engineering，2007，34(2):17 －23(in Chinese)

［17］盛骤，谢式千，潘承毅.概率论与数理统计［M］.4版.北京:高等教育出版社，2008:119－126 Sheng Zhou，Xie Shiqian，Pan Chengyi.Probability theory ＆mathematical statistics［M］.4th ed.Beijing:Higher Education Press，2008:119 －126(in Chinese)