领会意图 有效引领
缪仕本
[内容摘要]数学的心脏是问题,这道出了问题教学的重要性。因为有了问题,思维才有方向,才有动力。教师可以在承上启下处、知识盲点处、知识的联系处、揭示意义处、明确意图处、凸显本质处设问。
[关键词]学生;问题;有效;数学
数学的心脏是问题,这道出了问题教学的重要性。如何设计有效问题来引导学生学习呢?苏教版小学数学教材中的每一课都为师生的教与学提供了很多问题情境的素材,这些问题不仅是学生课前预习的触摸点,是课中学习的聚焦点,同时也是学生课后复习的附着点。因此,教师应依托问题情境,在吃透教材、领会意图的基础上,根据教学目标、教学内容和本班学生的实际设计若干个问题,把学生的思维直接引向问题中,使学生始终处于问题思考中,从而探索更多的新问题。本文以苏教版六年级上册《认识比》一课的教学实践为例,浅谈如何适时应用六个问题进行有效引领,以及这“六问”在教学中呈现的地位和作用。
一、问在承上启下处
小学数学知识前后联系紧密,教师可以根据原有知识来设计问题。课伊始,教师出示两杯果汁和三杯牛奶的情境图后问:“可以怎样表示这两个数量之间的关系?”这一问找准了新旧知识的联结点,问在了学生的认知起点上,不仅复习了旧知,而且能及时引入比的概念,起到承上启下的作用。在此之前,学生已会用减法比较两个数量之间的相差关系,也会用分数或除法比较两个数量之间的倍数关系。在学生回答的基础上,教师顺势切入:“其实两个数量之间的关系还可以用一种新的方法表示,想知道吗?”从而自然揭题:“这就是我们今天要学习的新知识——比。”
二、问在知识盲点处
教师在引导学生认识了比的名称、比号、比的前项、比的后项后,针对“2比3”和“3比2”问:为什么果汁与牛奶杯数的比中2是比的前项,而在牛奶与果汁杯数的比中2又是比的后项呢?这一问,问在了学生认知的盲点上,旨在帮助学生明确比是一个有序的概念,颠倒两个数量的位置就会得到另一个比,其意义也就不同。因为学生在初步表示两个数量的比时,经常容易混淆比的前后位置,通过此问可以有效引领学生主动进行观察比较,让学生认识到两个数的比是有顺序的。
三、问在知识的联系处
在教学例1后的“试一试”时,当师生讨论完“如果把每种溶液里的洗洁液看作1份,水分别可以看作几份?”这个问题后,教师追问:“还可以怎样表示每种溶液里洗洁液与水体积之间的关系呢?”这一问,问在知识的联结点上。在交流“还可以怎样表示每种溶液里洗洁液与水体积之间的关系?”的过程中,主要应启发学生用分数来思考,如洗洁液与水体积的比是1:8,也可以说洗洁液的体积是水体积的八分之一,这样可以使学生进一步感受比的意义,并初步体会比与分数的联系。
四、问在揭示意义处
教师指导学生完成“用比表示路程和时间的关系”的教学后,启发学生:仔细观察例1中的2:3和3:2,例2中的900:15和900:20,想一想:比与什么有关系?两个数的比可以表示什么?这一问问在了知识的本质点上,因为本课教学的关键就是让学生在现实的情境中理解比的意义,通过观察和分析,学生认识到上面的例子都是通过比来表示两个数相除的关系,在此基础上引导学生用自己的话说说对比的认识,进而描述出比的意义,两个数的比就是表示两个数相除。
五、问在明确意图处
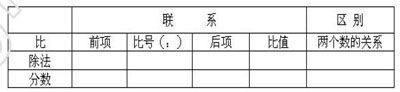
教师在教学例2后的“试一试”时,通过让学生把3:5分别改写成除法算式和分数后,组织学生观察:从这个等式中你还能发现什么?比的前项、比号、后项、比值分别相当于除法算式或分数中的什么?并出示如下表格让学生通过小组合作整理:
这一问问在了知识的异同点上,凸显了知识间的相互联系。学生运用已有的知识经验主动探索比与分数、除法的关系,使学生对比的认识更加完整,知识结构更加完善,同时在这个过程中进一步培养了学生观察、比较、概括以及合情推理的能力。
六、问在凸显本质处
教师引导学生讨论完第五个问题后,紧接着追问:比的后项可以为0吗?为什么?这一问问在了知识的本质上,重新唤醒了学生对“除数和分母不能为零”的回忆。除了继续巩固比与分数、除法之间的联系外,教师还可以与日常生活中体育比赛的比分(如某场足球赛的总比分为3:0)进行对比,使学生认识到倍比和差比之间的区别。
设问是一门科学,也是一门艺术。作为教师,可以从已知与未知的知识联系中引出问题,可以在重点与难点处制造问题,也可以于理论与现实的结合点处寻找问题。教师要想使问题真正成为数学的心脏,倡导问题式教学,就需要问得巧,应在备课的过程中对教材深思熟虑,真正领会文本的编排意图。让我们每位教师都共同努力,追本溯源、回归原点,成为教学的智者,正确解读文本。
(责任编辑 冯 璐)

