相位激光测距中相位测量与误差分析
邹孟成
(西安电子科技大学电子工程学院,陕西西安 710071)
由于激光具有较好的单色性、方向性、相干性和高亮度等特点,利用激光进行测距可以实现高精度测量。根据测量原理的不同,激光测距系统可分为脉冲式激光测距仪和相位式激光测距仪两类。脉冲式激光测距仪应用时间较早,在有合作目标配合的情况下可以实现较大距离的测量。但这种方法存在测量精度低的缺点。相位式激光测距仪通过测量连续幅度调制信号在待测距离上往返传播所产生的相位差,间接地测量信号传播时间,进而确定传输距离。这种方法通常具有很高的精度,可以达到毫米级[1]。
1 相位法激光测距的原理
相位法测距是通过测量相位差,间接测量传输时间t和传输距离L的两者关系[2]如下

其中

将式(2)带入式(1)得

式中,c为光波在空气中的传播速度;φ为调制信号经过L距离产生的相位差;f为调制信号的频率;N为正整数,表示调制信号波长的整数倍;Δφ为不足一个周期的相位差;λ为调制信号的波长。
在式(3)中,N不能通过单一频率的调制信号确定,在被测距离的情况下,可以确定N=0,此时

由式(4)可以看出,在调制信号频率f一定的情况下,Δφ的精度直接影响L的精度。
在激光测距系统中使用单片机A/D直接测量高频信号的相位比较困难,并且测量精度不高。为确保Δφ的精度,一般采用差频测相的方法[2,5],将高频信号与一个频率相近的信号进行混频,可以得到一个低频信号。对低频信号的相位测量比较容易,所测结果的精度也较高[5]。
2 差频信号相位测量原理
信号相位的获取一般方法是使用离散傅里叶变换(DFT)将时域信号转化到频域进行分析[3,9,11],在变换后的结果中选取特定点可以得到此离散频率下相位的正切值。再通过反正切函数就可以得到所需频率的相位值。此种方法还可以通过快速傅里叶变换(FFT)进行优化,以减少运算量和计算时间[5]。
上述方法具有通用性,在不要求精度和系统资源充裕的环境下可以直接应用,并且存在大量的资料指导设计。此方法同样可以用于激光测距的相位检测中,但考虑到激光测距系统的特点:所测信号的频率固定,较少的系统资源,本文将根据以上特点对以上方法进行优化和改进。
由于激光测距系统是在固定频率f下进行相位测量,因此通过调整激光测距系统的抽样频率fs,使两者满足如下关系

其中,m,k0为正整数;N为采样点数。

此时频域只有在点m,N-m处有值,其余部分为0。因此只需进行第 m 点运算[3-5]。
在激光测距系统中,相对于整数运算,进行浮点运算和三角函数运算需要更多的时钟周期。因此在满足系统精度的前提下,将范围内的正弦和余弦值进行量化[5],并保存在程序中,需要时通过查表求得,避免重复运算。
相位的提取一般使用反正切函数,数学库提供的反正切函数都具有较高的精度和较好的错误处理机制,但资源的消耗也是巨大的[6]。C标准库中反正切函数在单片机上运行将耗费几千个时钟周期,并且容易导致堆栈溢出的错误。因此必须重新设计反正切函数,使其在满足精度的情况下,消耗更少的资源。
反正切函数必须能处理(-∞,+∞)范围内的数据,利用下式可以将处理范围缩小到[-1,1]。
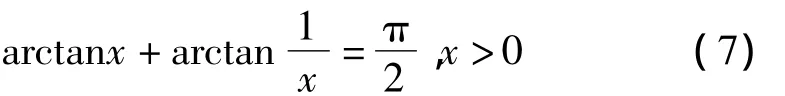
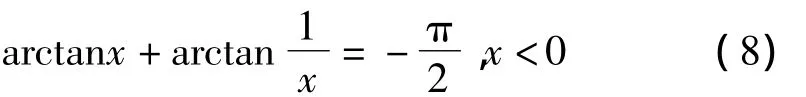
反正切函数可以使用多项式逼近,包括泰勒级数,切比雪夫多项式和欧拉反正切公式[6]。为得到计算速度较快的反正切函数,必须使用收敛速度较快的多项式。泰勒级数收敛速度较慢,给定误差ε=10-4,泰勒级数需要展开5 000项,因此泰勒级数不适合在激光测距系统中使用,而切比雪夫多项式和欧拉反正切公式都具有较快的收敛速度[6]。
欧拉反正切公式[7]
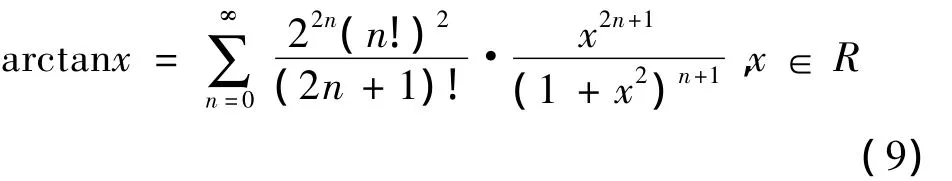
切比雪夫多项式[8]
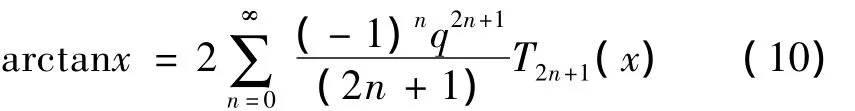

图1 切比雪夫多项式与欧拉反正切公式逼近结果对比
如图1所示,欧拉反正切公式在绝对值接近于1时误差显著增大,而切比雪夫多项式在[-1,1]范围内误差均<8×10-4rad,具有更平稳的误差分布。同时相比于切比雪夫多项式,欧拉反正切公式需要进行更多的运算。因此,选用切比雪夫多项式作为反正切函数的实现是较好的选择。根据实际需求,通过增加或减少切比雪夫多项式的次数可以控制逼近结果的精度。图2所示为切比雪夫多项式取不同数目项进行逼近结果的对比,从图中的对比结果可以看出,每增加一项,逼近结果的精度可以提高一个数量级。通过以上仿真结果分析可以得到如下结论:对比其他方法,使用切比雪夫多项式进行逼近,可以获得更快的收敛速度,并且在[-1,1]范围内,误差的分布更加平稳。
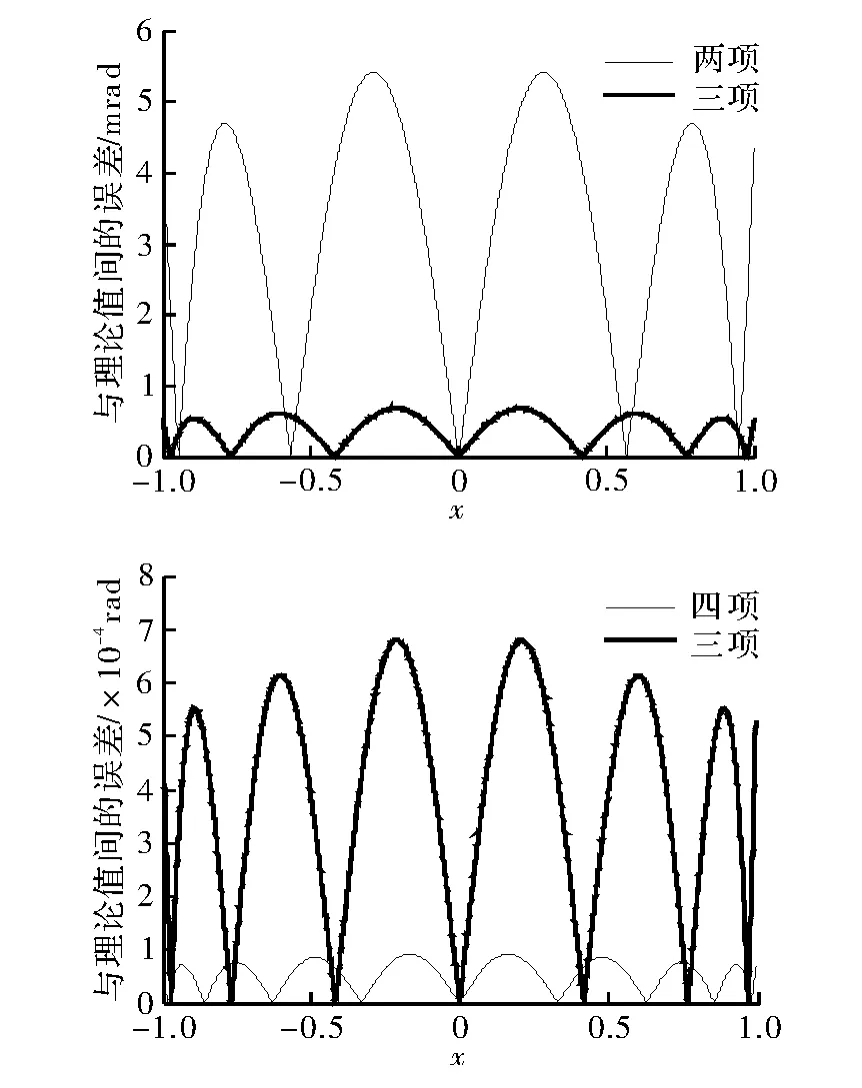
图2 切比雪夫多项式取不同项数逼近结果对比
3 差频信号相位测量实现
图3所示是相位测量的流程。在激光测距仪系统中A/D模块完成对数据的采集和量化后,通过中断调用完成离散傅里叶变换第k点值的计算。根据计算结果求得相位的正切值。
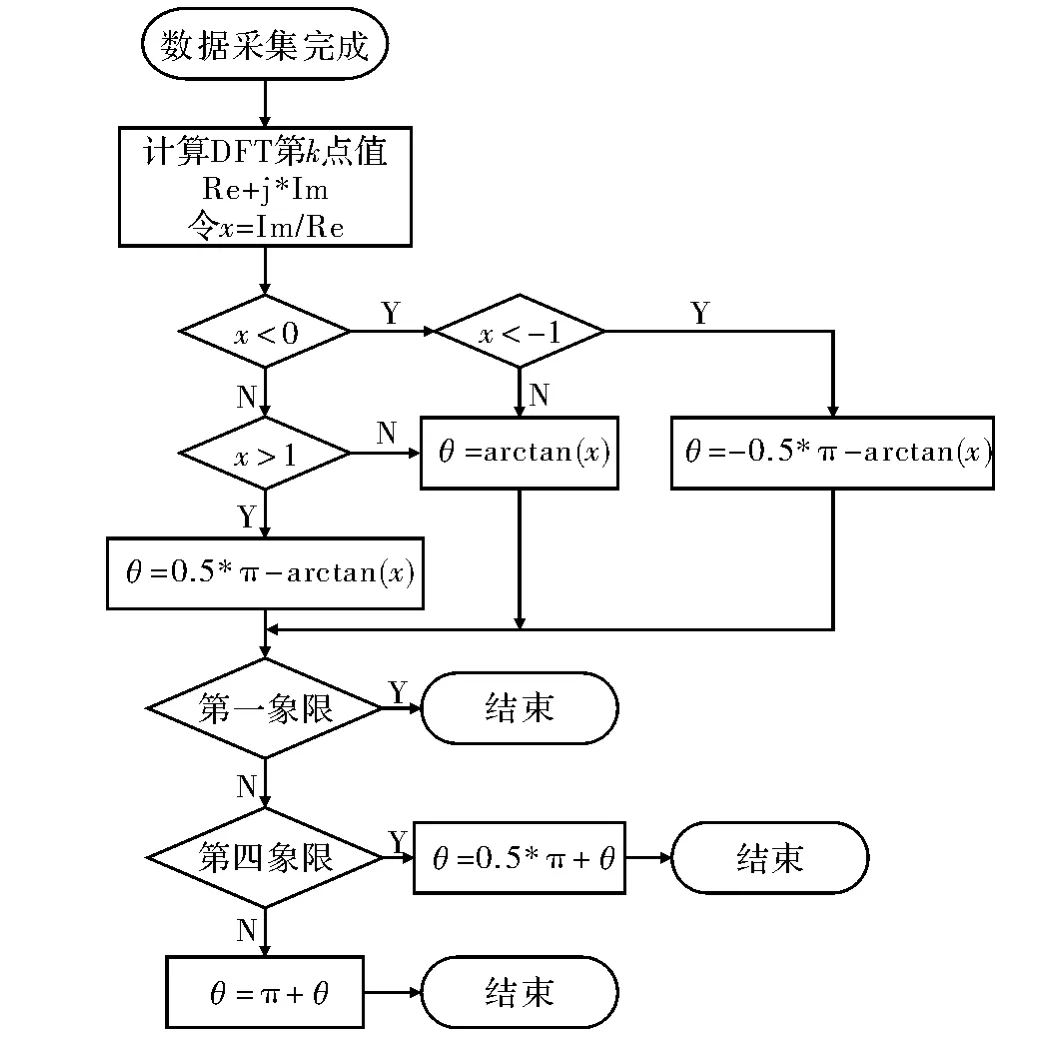
图3 差频信号相位测量流程图
在激光测距过程中,信号相位是在[0,2π]连续变化的,而反正切函数的值域为,因此必须根据DFT的结果对反正切函数进行修正[10]。首先对绝对值>1的正切值应用式(7)或式(8),并调用反正切函数完成对相位的计算。然后根据DFT实部和虚部的符号判断相位所在的象限,完成对正切值的修正。使得到的相位值在[0,2π)连续变化,避免在处相位的跃变。
4 结束语
图4为利用本文所提方法得到的相位值与理论值之间的误差,由本方法得出的结果在不同相位值上的误差呈现一种震荡的形式,总体维持在8×10-4rad以下的水平。

图4 仿真结果与理论值在不同相位处误差
通过仿真验证,利用本文所提方法在消耗较少资源的情况下,得到满足精度需求的结果。从仿真结果看,相位的最大误差<8×10-4rad,在测尺为1 m的情况下,距离测量的精度可达0.8 mm,可以满足一般情况下高精度测量。同时,使用不同测尺进行组合,可以提高测量的最大距离[1,4-5,10]。
[1]孔东.相位法激光测距仪的研究[D].西安:西安电子科技大学,2007.
[2]徐恒梅,付永庆.相位法激光测距系统[J].应用科技,2010(6):20-22.
[3]史林,赵树杰.数字信号处理[M].北京:科学出版社,2011.
[4]张啸.手持式激光测距仪的研究与设计[D].合肥:合肥工业大学,2010.
[5]丁艳.相位法激光测距仪设计及其关键技术研究[D].上海:同济大学,2007.
[6]伍微,刘小汇,李峥嵘,等.实现定点DSP汇编层反正切函数的差分进化算法[J].系统工程与电子技术,2005(5):926-928.
[7]魏静,邓勇.欧拉反正切公式的一个新证明[J].伊犁师范学院学报:自然科学版,2010(2):14-16.
[8]STEVEN W K.Calculating atan2(y,x)using chebyshev polynomial approximation[M].Newyork:Mathworks Inc,2009.
[9]BOSCH T.Crosstalk analysis of 1 m to 10 m laser phase -shift range finder[J].IEEE Transactions on Instrumentation and Measurement,1997,46(6):1224 -1228.
[10]SUNGUI H,JUNHWAN J,KYIHWAN P.Solving 2pi ambiguity problem of a laser scanner based on phase-shift measurement method for long distances measurement[C].Chongqing:2012 12th International Conference on Control,Automation and Systems,2012.
[11]SUN Wenjun,SUN Jingnan,BU Wenbin,et al.New phase measurement method for laser range finder[C].Shanghai:Proc.SPIE 7656,5th International Symposium on Advanced Optical Manufacturing and Testing Technologies,2010.

