扩散方程高精度加权差分格式的MATLAB实现
胡 敏
(攀枝花学院 数学与计算机学院,四川 攀枝花617000)
0 引言
MATLAB是一款具有精确数值计算功能和丰富图形处理函数的软件,[1]偏微分方程的数值解可直观地以二维、三维图形方式显示在屏幕上.因此,近年来,越来越多的人开始使用MATLAB来求解偏微分方程.[2-7]一维扩散方程是最简单的偏微分方程之一,其定解问题的数值方法有差分法、有限元法和边界元法.本文主要讨论一维扩散方程的一个高精度加权差分格式的MATLAB实现.[8]
1 求解扩散方程的基本思想
用有限差分法求解偏微分方程问题必须把连续问题进行离散化,因此求解扩散方程的基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点.[9]
把连续定解区域上连续变量的函数用定义在网格上的离散变量函数来近似,于是原微分方程和定解条件就近似地以代数方程组代之,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解.然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解.[10]
2 扩散方程的高精度加权差分格式
一维扩散方程
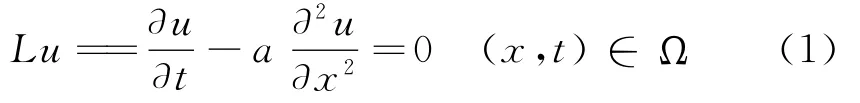
其中,扩散系数a为常数.先进行网格剖分,取空间步长h和时间步长τ,用两族平行直线x=xj=jh(j=0,1,…,N)和t=tk=kτ(k=0,1,…,M)(其中N,M 都是正整数)将矩形域分割成矩形网格,网格节点为 (xj,tk).用ukj表示定义在网点 (xj,tk)的函数,0≤j ≤N,0≤k ≤M.
利用二阶微商三次样条四阶逼近公式[11]有

其中 (uxx)j表示二阶偏导数uxx在点 (jh,t)处的近似值.
由于方程(1)在整个求解区域内成立,于是将(2)式代入(1)式得

由于(3)式在任意时刻均成立,则

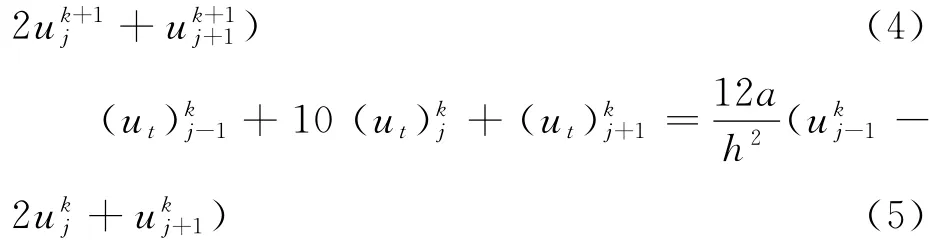
将(4)式和(5)式分别乘以θ和1-θ(0≤θ≤1),再相加得

又因为

于是得高精度加权差分格式[8]
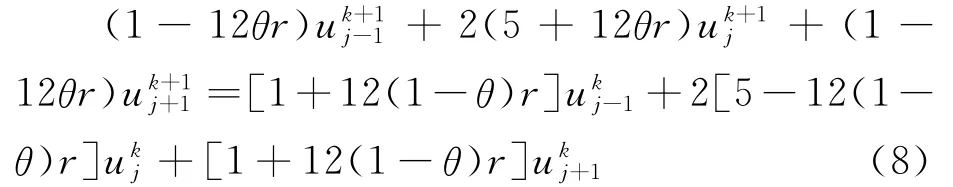
3 高精度加权差分格式的MATLAB编程
利用上述高精度差分格式求扩散方程的近似解,需要求解一个大型稀疏矩阵方程组,这时采用迭代法是最合适的,而且计算出的结果也比较精确,且其程序设计简单,能有效地解决一些高阶问题,是解大型稀疏方程组的一种重要方法.本文采用高斯-赛德尔(Gauss-Seidel)迭代法来实现扩散方程的高精度加权差分格式所构造的稀疏矩阵方程组的求解.
%解一维扩散方程 格式 (Ut-aUxx=0,a>0)
%用g-s(高斯-赛德尔)迭代法解
%m,n为x,t方向的网格数
format long
syms temp1;
syms temp2;
syms temp3;
a=1;
l=pi;
T=pi^2;
N=10;
M=200;
h=l/N;
to=T/M;
r=(a*to)/h^2;
for j=1:N+1
x(j)=(j-1)*h;
for k=1:M+1
t(k)=(k-1)*to;
u0(j,k)=exp(-t(k))*sin(x(j));
end
end
u0 %求解精确解u0
for j=1:N+1
x(j)=(j-1)*h;
u1(j,1)=sin(x(j));
u2(j,1)=sin(x(j));
u3(j,1)=sin(x(j));
end
for k=1:M+1
t(k)=(k-1)*to;
u1(1,k)=0;u1(N+1,k)=0;
u2(1,k)=0;u2(N+1,k)=0;
u3(1,k)=0;u3(N+1,k)=0;
end
for k=1:M
for j=2:N
temp1=((1+9*r)*(u0(j-1,k)
+u0(j+1,k))+(10-18*
r)*u0(j,k)+...-(1-9*
r)*(u0(j-1,k+1)+u0(j
+1,k+1)))/(10+18*
r);
u1(j,k+1)=temp1;
temp2=((1+6*r)*(u0(j-1,k)+
u0(j+1,k))+(10-12*r)*
u0(j,k)+...-(1-6*r)*
(u0(j-1,k+1)+u0(j+1,k
+1)))/(10+12*r);
u2(j,k+1)=temp2;
temp3=((1+3*r)*(u0(j-1,k)+
u0(j+1,k))+(10-6*r)*
u0(j,k)+...-(1-3*r)*
(u0(j-1,k+1)+u0(j+1,k
+1)))/(10+6*r);
u3(j,k+1)=temp3;
end
end
u1 %求解数值解u1
u2 %求解数值解u2
u3 %求解数值解u3
for k=1:M+1
for j=1:N+1
R1(j,k)=abs(u0(j,k)-u1(j,k));
R2(j,k)=abs(u0(j,k)-u2(j,k));
R3(j,k)=abs(u0(j,k)-u3(j,k));
end
end
R1,R2, R3 %计算误差R1,R2, R3
Rmax1=max(R1) %求误差R1的最大值
Rmax2=max(R2) %求误差R2的最大值
Rmax3=max(R3) %求误差R3的最大值
%精确解与数值解的比较:
x=0:0.1:1;
hold on
plot(x,u0(:,M+1),'b');
plot(x,u1(:,M+1),'y');
plot(x,u2(:,M+1),'r');
plot(x,u3(:,M+1),'g');
title('t=1,h=0.1,τ=0.005时精确解和数值解的比较')
hold off
4 运行结果分析
考虑扩散方程混合问题
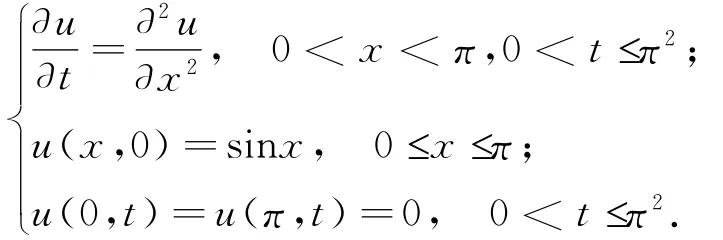
其解析解为u(x,t)=e-tsinx.
取r=0.5,θ=0.25,θ=0.5和θ=0.75代入高精度加权差分格式(8)计算数值解,在某时刻的最大误差分别记作e1,e2,e3,数据如表1.
在同一个坐标系中,绘出二维图作比较,如图1.

表1 某时刻的最大误差

图1 数值解与精确解的比较
从表1和图1可以看出,当θ=0.5时,误差最小;并且当网格分得越小时误差更小.建议在解决实际问题时选择误差小的格式进行分析求解.
[1](美)Stephen J,Chapman.MATLAB编程[M].邢树军,郑碧波译.北京:科学出版社,2008:3.
[2]王 飞,裴永祥.有限差分方法的 MATLAB编程[J].新疆师范大学学报:自然科学版,2003(4):21-27.
[3]赵德奎,刘 勇.MATLAB在有限差分数值计算中的应用[J].四川理工学院学报,2005(4):61-64.
[4]田 兵.用 MATLAB解偏微分方程[J].阴山学刊,2006(4):12-13.
[5]谢焕田,吴 艳.拉普拉斯有限差分法的 MATLAB实现[J].四川理工学院学报,2008(3):1-2.
[6]史 策.热传导方程有限差分法的 MATLAB实现[J].咸阳师范学院学报,2009(4):27-29.
[7]薛 琼,肖小峰.二维热传导方程有限容积法的 MATLAB实现[J].计算机工程与应用,2009(4):27-29.
[8]田振夫,张艳萍.扩散方程的高精度加权差分格式[J].中国科学技术大学学报,1999(2):237-241.
[9]陈金甫,关 治.偏微分数值解法:第二版[M].北京:清华大学出版社,2004:274.
[10]李瑞遐,何志庆.微分方程数值方法[M].北京:华东理工大学出版社,2005:97.
[11]田振夫.泊松方程的高精度三次样条差分方法[J].西北师范大学学报:自然科学版,1996(2):13-17.

