一种带有连续变化分辨率的中央凹视觉处理方法研究

李金伦，崔少辉，徐 帅

（军械工程学院导弹工程系，河北 石家庄 050003）

0 引 言

近年来，单个图像传感器的分辨率已达几亿像素。在采集如此高分辨率图像的同时对计算机实时处理的性能就会产生明显的影响。因此，对于图像处理系统而言，面临着如何解决实时处理高分辨率图像的问题。事实上，在一些应用中，例如跟踪和模式识别、图像传感器传输进来的宽视角、大范围、高分辨率图像并不是需要利用图像的所有的区域，更多的仅仅是对图像中某一部分要求较高的分辨率；因此，就产生了高分辨率图像采集与实时处理能力不足之间的矛盾。

为解决以上问题，常采用多分辨率处理技术，如中央凹传感器，这种传感器的表面分布着分辨率不均匀的感光元件。应用该传感器时，需要确保最有用的区域被放在高分辨率范围内，一般该范围为传感器的中心区域[1]。

模式识别与跟踪是中央凹传感器成功应用的两个领域。文献[2]在解决模式识别问题，以及文献[3-4]在解决跟踪问题时都应用了中央凹传感器。但是，中央凹传感器的一大缺点就是不可以动态重构，为了保持高分辨率区域始终对准目标，不得不应用机械装置来实时控制传感器的朝向，显然对于快速移动目标，该方法难以满足实时性。目前，应用电子元器件构造嵌入式系统进行中央凹的动态重构成为较为普遍的方法。

本文基于后一种解决方案，提出了一种可以适用于非定制CMOS单一分辨率图像传感器的中央凹视觉处理方法。实验表明：该方法可以提供更大的中央凹区域。

1 相关工作

许多文献都介绍过多分辨处理技术，灵感大多来源于人类视觉，即人眼视网膜中的光感受器单元和神经节细胞的分布是非均匀的，在中央凹部分高度密集而周边稀疏，这种特性使视觉信息的获取是非均匀的。中央凹部分具有很高的视敏度，但稍微偏离一点，视敏度就会急剧下降，离开中央凹5°，视敏度将下降50%。文献[1]基于人类视网膜原理提出对数极坐标映射的方法，文献[5]在分析比较的基础上设计了一种晶格形状，可以在晶格内应用对数极坐标进行映射。

虽然对数极坐标原理已经广泛地应用于多分辨映射中，但采用极坐标系统描述的中央凹区域，因其具有非线性缺陷，并不能很好的匹配视网膜，而且在中心位置会产生盲点。

文献[6]采用了一种基于多分辨技术的小波变换方法，这种方法通过使用低通和高通滤波器使得在数据传输过程中可以良好地保持线性。

相对于有固定分辨率的图像传感器，研究更倾向于提供更多中央凹区域，文献[7]提出了一种多分辨结构，其中央凹区域可以像眼球一样扫视。文献[8]在这种方法的基础上构建了多个中央凹区域来进行移动物体的识别。

在总结前人工作的基础上，本文基于可分离映射，提出了一种带有连续变化分辨率的中央凹视觉处理方法。

2 基本原理

为了避免使用全景遥感摄像头，可以采用带有宽视角的高分辨率CMOS传感器。然而，仅仅需要读取其中很小的一部分窗口区域，而且这个窗口可以在程序的控制下移动，这就提供了一种全景摇感的等价方式，因为窗口可以从一个位置很快地移动到另一个位置。由于摄像头并没有移动，因此，不会出现由摄像头的移动所带来的图像模糊等问题。

虽然在使用流水处理时，一幅高分辨率的图像很容易在FPGA上进行实时处理。然而，任何需要多帧图像的算法都需要相当多的片外存储器和很大的存储器带宽。为了使能片内存储器，必须减少数据的体积和图像的尺寸。

简单地通过降低分辨率来减小数据规模会导致严重的信息丢失。在很多应用领域中（例如跟踪与模式识别），只有图像的一个小区域中要求高分辨率。解决该问题的一个方法是使用中央凹窗口。受人类视觉系统启发，这种方法在视网膜中央凹保持高分辨率，同时可降低周围的分辨率。

基于该机制的视网膜中央凹视觉系统如图1所示。该系统对窗口中的像素进行了中央凹映射，以得到降低了分辨率的图像。此后该图像得到处理，从而得到需要的数据并为下一帧图像确定最佳位置，以便在CMOS传感器中重新对窗口进行定位。

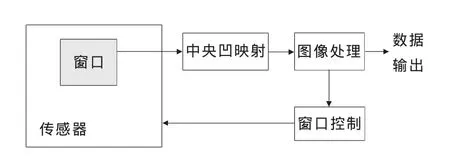
图1 使用中央凹映射的结构

3 中央凹映射方法

相对于使用基于极坐标系统下的对数极坐标映射，更主张在笛卡尔坐标系下进行图像变换。设u为到输入图像中心的距离，f为到中央凹图像中心的距离。此时的中央凹映射也可以认为是前向映射的一种。

其逆向映射为

放大率M，被定义为输入与输出像素距中心距离的比率

与放大率相关的要素是像素有效分辨率A，其由映射斜率的大小决定

因为映射方程必须是单调的，所以得出

映射一个N×N的输入图像到w×w的输出图像时，需要满足如下关系：

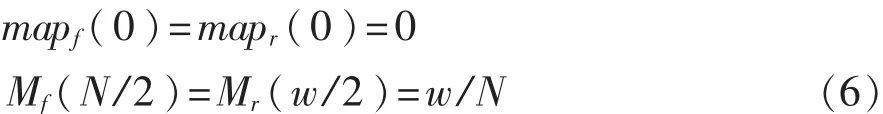
尽管中央凹图像的分辨率与输入图像不同，而且最高分辨率的图像也不一定在图像中心。但是为了方便说明，本文以中央凹在图像中心为例，此时需要满足：

另一个需要考虑的问题就是如何来定义距离u和f，因为不同的定义会产生不同程度的图像变形。以图像中心为原点，可以得到输入和输出图像的坐标（xu，yu），（xf，yf）。

采用De距离时，可以得到

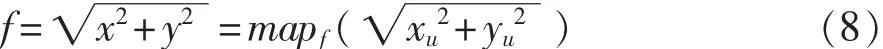
因为在径向映射中，每个像素点关于坐标轴的角度是不变的，这就意味着x、y与放大率之间存在以下关系

采用D8距离时，可以得到计算更简单的转换方法：

考虑到可分解映射时，可以得到一个更加简单的转换方法，并且可以对x和y进行单独映射

在每一种坐标系中，可分解映射都会有不同的放大率[1]。

图3比较了N=512，w=64，M=1/8时3种映射的差别，其中（c）、（d）、（e）有相同的放大率，这里为了便于观察，对64×64的图像进行了放大。

通过观察可以发现，采用D8距离变换的图像（c），画面明显带有锥度感，这与D8距离的定义是分不开的：

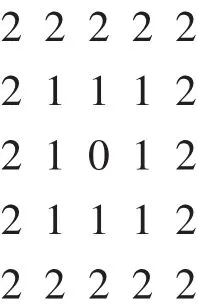
图像（e）的变换采用了De距离变换，由于De距离的定义为

图像（e）的变换明显带有弧度感。

虽然（f）与（d）都是基于可分解映射，但明显图像（f）提供了更大的中央凹区域：

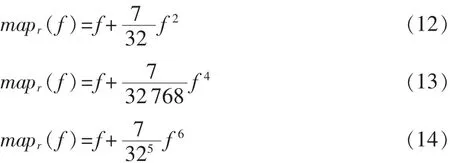
公式中系数的确定是为了使映射后图像的尺寸固定。

图2显示了两种不同灵敏度的映射，可以看出4次方和6次方分量的采用增大了中央凹区域面积，并且6次方可以带来更明显的变化，而且其外围无效数据的分辨率更低。但是在实际应用中，并不需要如此大的中央凹区域，采用式（14）的同时也会带来6次方分量计算数据较大等问题。所以，本文更倾向于选择式（13）的方法。

在中央凹图像中，虽然图像边缘的横向或纵向轮廓产生了明显扭曲，但中央凹区域变形却很少。因此，映射后，由于边缘图像数据的丢失，整个图像的数据量下降了。

4 应用领域

本文提出的方法可以应用在一些计算机视觉领域，例如跟踪、模式识别和图像压缩等。应用于前两种领域时，中央凹区域应对准感兴趣的目标，以便后期的识别与跟踪。当目标从中央凹区域内开始移动时，系统就可以很快的察觉，并根据目标所在位置进行算法的快速重构以保证具有高分辨率的中央凹区域始终对准目标。

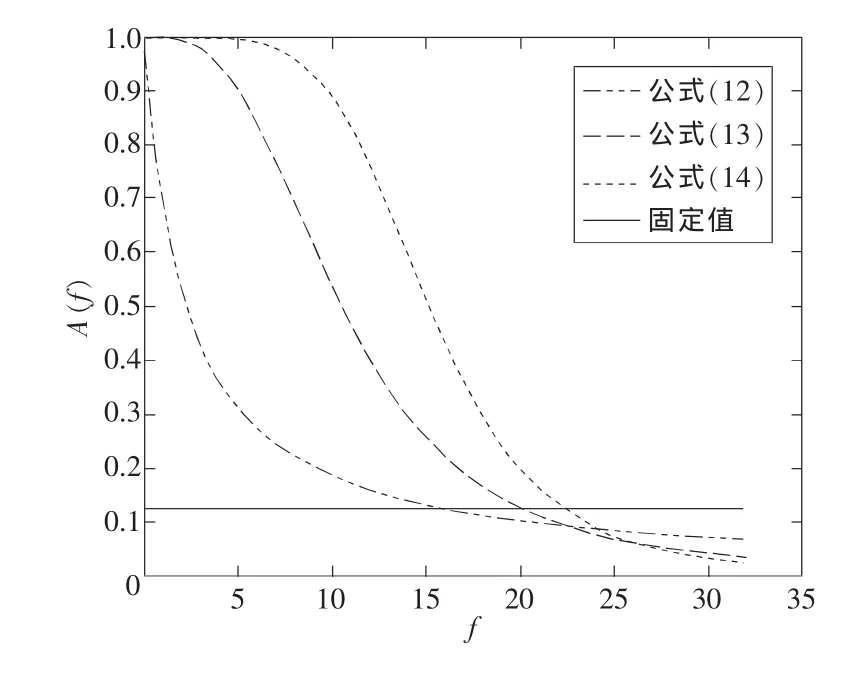
图2 不同中央凹映射的有效分辨率变化曲线

图3 中央凹映射举例

另外，在移动物体捕获方面也可以应用中央凹视觉映射[10]。这种方法同样是模拟了人类，即人类的视网膜周边部分虽然对识别细小的物体不起作用，但对给光撤光以及物体运动等刺激是敏感的，如果外界的一部分急速发生变化，则与此对应的视网膜周边部分就会迅速起反应，眼球随之产生运动，使视轴朝向那个感兴趣的方向。

5 结束语

本文介绍了几种带有连续变化分辨率的中央凹映射，通过对比，得出一种较优化的解决方法。该方法可以提供更大的中央凹范围，并在保持中心有效区域分辨率的同时，通过降低图像边缘无效区域的分辨率来达到减少图像数据量的目的，进而可以达到缩小存储量、减少图像处理时间，以更好的满足实时性处理要求。本方法在模式识别、跟踪等领域有良好地应用前景，未来的研究将会聚焦于中央凹图像处理技术。

[1] Donald G B.基于FPGA的嵌入式图像处理系统设计[M].原魁，何文浩，译.北京：电子工业出版社，2013.

[2]Wilson J C，Hodgson R M.A pattern recognition system based on models of aspects of the human visual system[C]∥International Conference on Image Processing and its Applications.Maastricht，1992：258-261.

[3] Xue Y，Morrell D.Adaptive foveal sensor for target tracking[C]∥Thirty-Sixth Asilomar Conference on Signals Systems and Computers Pacific Grove，2002：848-852.

[4] Cui Y， Samarasekera S， Huang Q， et al.Indoor monitoring via the collaboration between a peripheral sensor and a foveal sensor[C]∥IEEE Workshop on Visual Surveillance Bombay，1998：2-9.

[5] Traver V J，Pla F.Designing the lattice for log-polar images[C]∥11th International Conference on Discrete Geometry for Computer Imagery Naples，2003：164-173.

[6] Wei J，Li Z N.On active camera control and camera motion recovery with foveate wavelet transform[C]∥IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23（8）：896-903.

[7]Camacho P， Arrebola F， SadovalF.Shifted fovea multiresolution geometries[C]∥International Conference on Image Processing Lausanne，1996（1）：307-310.

[8] Camacho P， Arrebola F， Sadoval F. Multiresolution sensors with adaptive structure[C]∥24th Annual Conference of the IEEE Industrial Electronics Society Aachen，1998（2）：1230-1235.

[9] Rafael C G.数字图像处理[M].2版.阮秋琦，阮宇智，译.北京：电子工业出版社，2007.

[10]Liu Y， Bouganis C S， Cheung P Y K.A spatiotemporal saliency framework[C]∥EEE International Conference on Image Processing Atlanta， 2006：437-440.