火力发电厂大管径液体流量测量新方法研究

潘宏刚，张 凯，李 亮，王 飞，刘 凯

(沈阳工程学院 a.能源与动力学院;b.学报编辑部，辽宁沈阳110136)

近年来，在能源与资源工业，特别是火力发电厂中出现了大管径液体流量的测量问题.由于火力发电厂大管径管道的流动特性很难掌握和测量，而流量测量又是工业计量的组成部分之一，就像工业生产的眼睛，对工业生产和能源节约都非常重要.因此，流量的准确测量特别是火电厂大管径液体流量的准确测量，对机组的安全稳定运行、水资源的节约和经济效益的提高都有积极作用.通过阅读大量相关文献和对各种流量检测方法的深入了解，火电厂大管径液体测量方式有很多，虽然每种流量计都有其优点，但也都有其局限性，至今没有一种对于大管径流量测量没有任何缺憾的方法.综合以上诸多因素，在此提出了研究大管径流量测量的新方法，即根据主管道和分支管道在不同负荷下流量特性关系，通过描绘曲线和计算得出两者的关系，最终利用小管道流量特性反映出大管道流量特性.通过实验后对其误差进行的详细分析，使实验结果更具有说服力.

1 测量原理及主要设备

1.1 测量原理

试验装置原理如图1所示，实物如图2所示.泵从地下水池中抽水，出水分为3个支路，其中中间的为主管道不设阀门，两端的为分支管道1和分支管道2设有阀门，出水排到联合水箱(用隔板分为3个独立的水箱)，水箱外设有水位计.

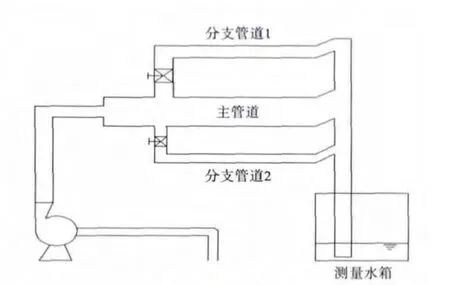
图1 试验装置原理

图2 试验装置实物

从2个水箱引出水位计，旁边放一秒表，在设定的工况下，通过相机记录下不同时间的水位高度，利用公式(水箱截面积×高度差/时间差=体积流量)确定流量，同时采用多点计算取平均值的方法保证精确度.计算出主管道与不同直径分支管道的流量，根据电动机的频率与泵的转速成正比，则主管道内的流量变化值100%、90%、80%、70%、60%、50%所对应的电动机的频率分别为 50 Hz、45 Hz、40 Hz、35 Hz、30 Hz、25 Hz，以此为基准点，通过调节变频器来实现对主管道流量负荷的控制.然后，绘出在不同的频率下(从高到低)主管道和各分支管道之间的流量比关系.

1.2 主要设备

循环水泵:型号1R100-80-125，扬程20 m，流量100 m3/h，允许吸上真空高度5.5 m，额定转速2 900 r/min，效率70%.

管道和水箱尺寸分别见表1、表2.

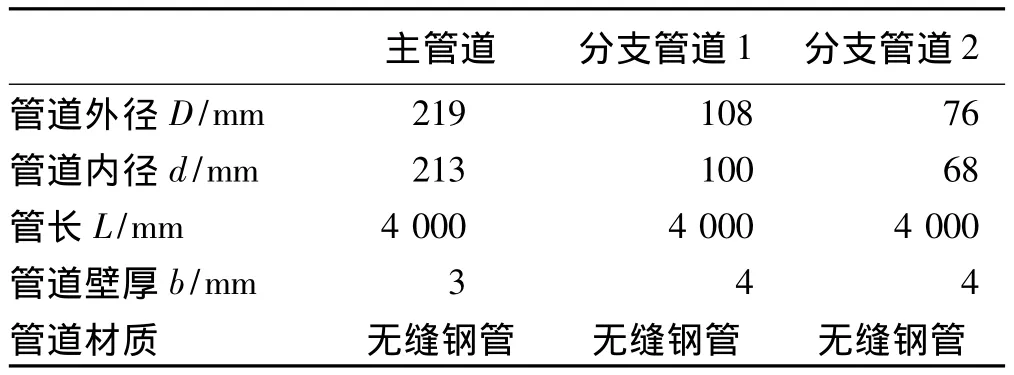
表1 管道尺寸

表2 水箱尺寸

2 数据测量与分析

2.1 数据测量

主要测量主管道与分支管道在不同负荷情况下的流量，得出主管道与分支管道之间的流量关系.流量测量采用的方法:主管道与分支管道1同时启动，关闭分支管道2，其测量数据如表3所示;主管道与分支管道2同时启动，关闭分支管道1，其测量数据如表4所示.

表3 主管道与分支管道1同时启动，关闭分支管道2时的测量数据

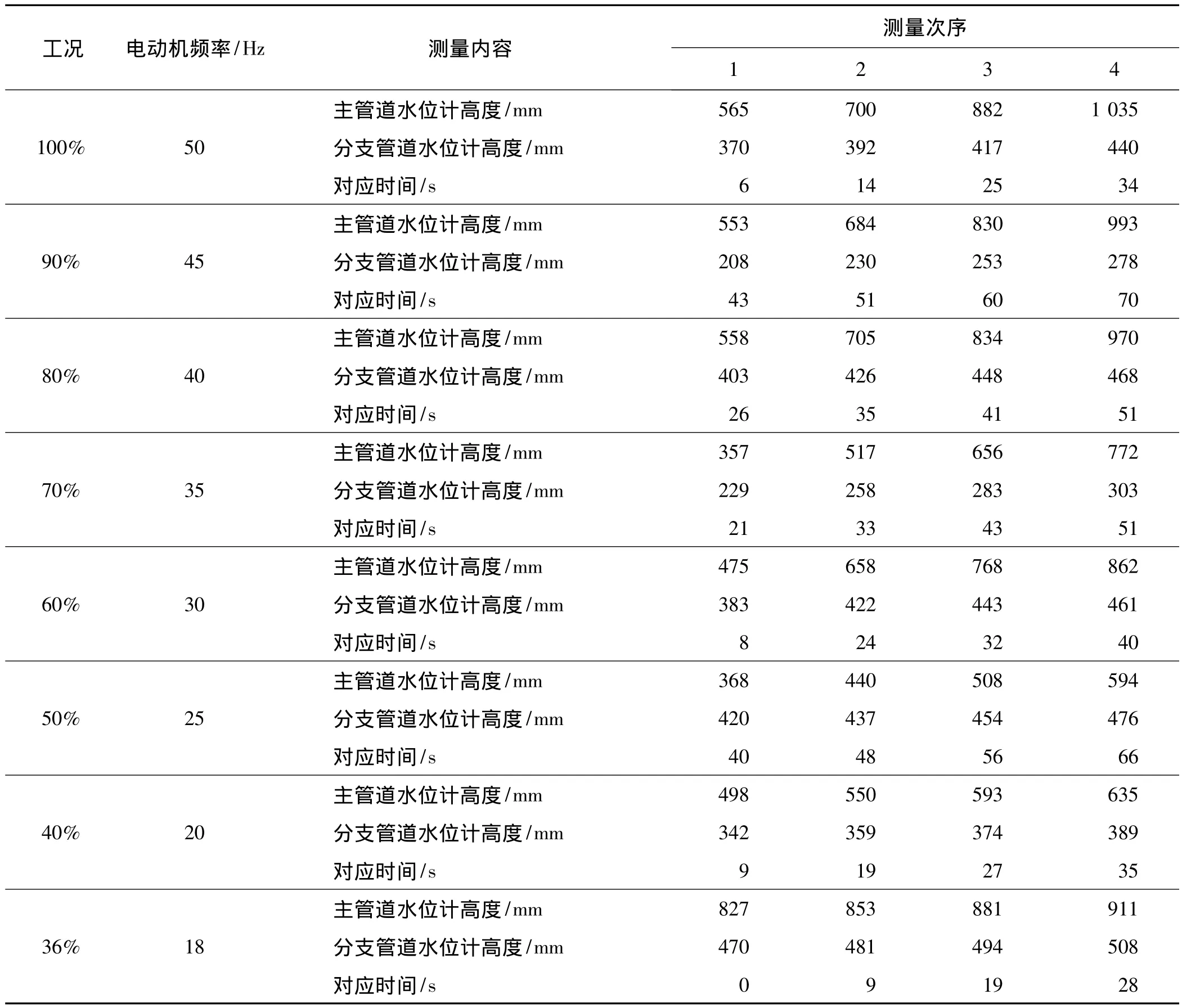
表4 主管道与分支管道2同时启动，关闭分支管道1时的测量数据

2.2 数据分析

实验过程是利用体积法来测量各管道的流量，然后利用差值法求出水位计高度与对应时间的线性关系，再取其平均值来降低读数过程中人为因素造成的误差，即可得到水箱内液面上升的速度，通过V·A=qv得出管道内流量.当只开主管道和主管道与分支管道1同时开启时测得的流量见表5，不同负荷下2种工况对应的流量曲线关系如图3所示.

表5 只开主管道与主管道和分支管道1同时开启时的流量之和及流量关系

在不同负荷下，测得主管道与分支管道1之间的流量关系如表6所示，流量随负荷变化曲线如图4所示，主管道与分支管道1流量比值与工况之间的曲线关系如图5所示.

在不同负荷下，测得主管道与分支管道2之间的流量关系如表7所示，流量随负荷变化曲线如图6所示，主管道与分支管道2流量比值与工况之间的曲线关系如图7所示.

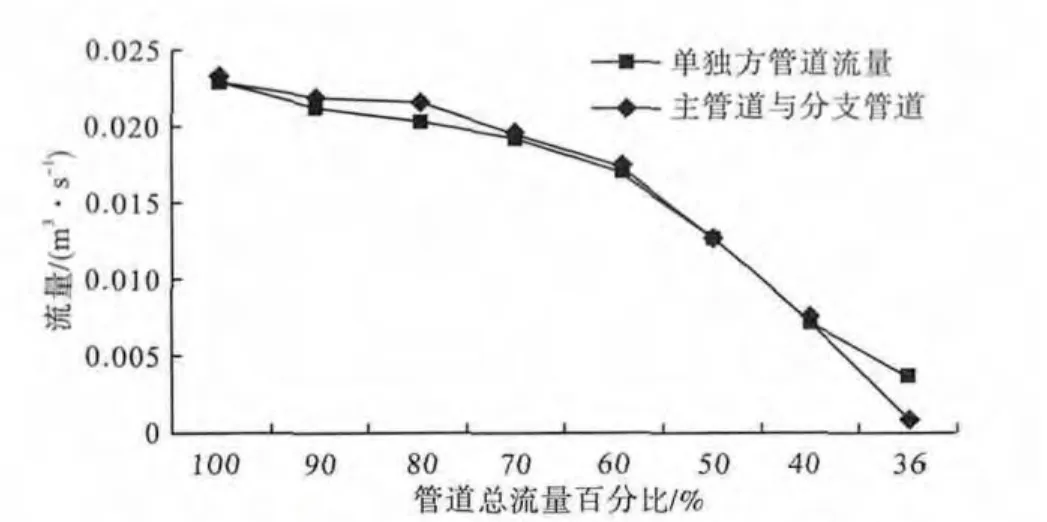
图3 管道总流量在不同工况下的曲线关系

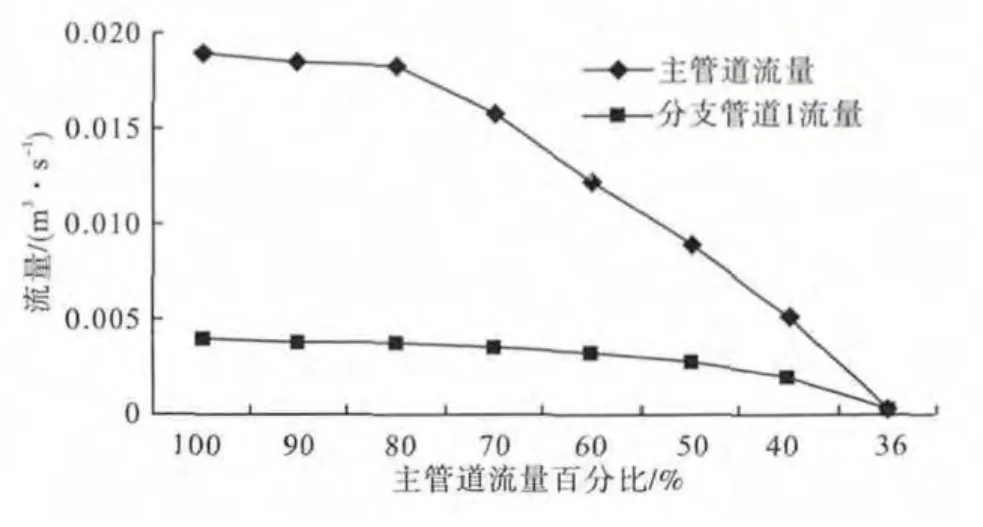
图4 主管道与分支管道1在不同工况下的流量关系曲线

表6 主管道与分支管道1的流量关系

表7 主管道与分支管道2的流量关系表

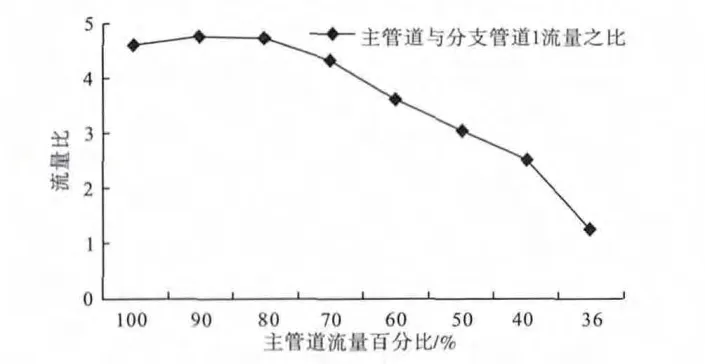
图5 主管道与分支管道1流量比值与工况之间的曲线关系

图6 主管道与分支管道2在不同工况下的流量关系曲线

截取图5和图7中主管道流量40%到80%段绘于同一坐标系里，如图8所示.

图7 主管道与分支管道2流量比值与工况之间的曲线关系

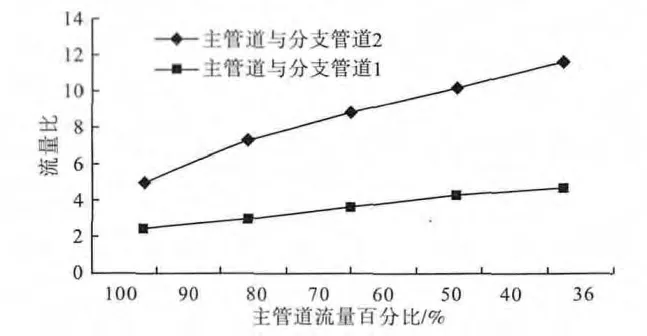
图8 主管道与分支管道1、2流量比值随工况变化的曲线

3 试验结果分析

当主管道水流量从高负荷到低负荷变化时，主管道与分支管道之间的流量特性曲线间的距离呈先平行后减小的趋势.当主管道流量低于80%额定流量时，主管道流量特性曲线开始发生明显的下降趋势.

主管道负载在40%至80%段时，所对应的流量之比基本呈直线变化，2条直线斜率分别为0.412和0.137，与水平轴的夹角分别为 22.4°和 7.8°.可见管径差距越大，直线斜率就越大，即流量之比随着管径之比的增大而增大.当主管道与分支管道管径相同时，管径之比为1，斜率为0，即一条水平直线y=1，所以流量之比变化关系应遵循方程y=kx+1.由于不同管径对应不同的斜率k，因此可通过测量不同管径比时的流量关系得到k值，从而得到流量比与管径比之间的对应关系.其形成如表8所示，对应的曲线关系如图9所示.

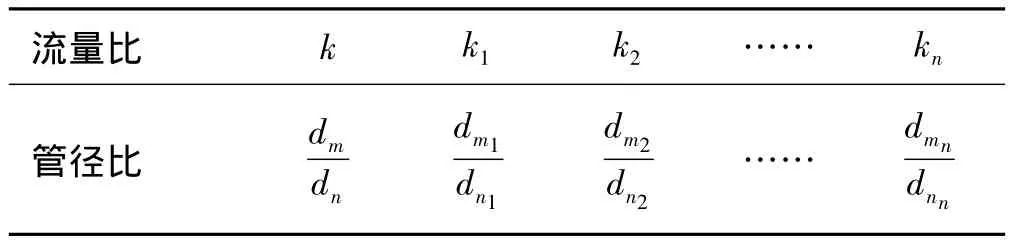
表8 流量比与管径比之间的关系

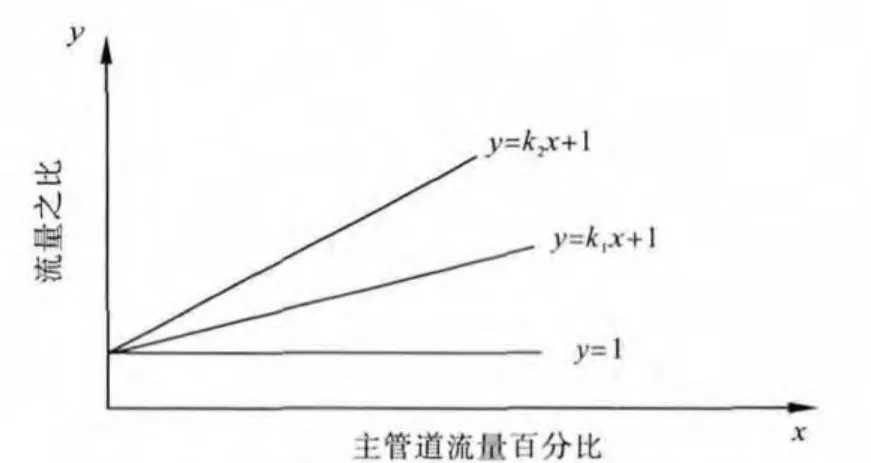
图9 不同管径比的流量比关系曲线

由表8可根据未知主管道流量的管径之比得到流量之比，再由小管径流量和流量之比得出大管径内流体流量.

4 实验结论

综上所述，分别求出主管道与分支管道的临界流量，则主管道与分支管道的最大流量比可以确定，在流量之比坐标图中找到对应的最大流量比的点，然后连接其与(0，1)点即可形成流量之比的变化关系曲线，根据最大流量比的点与(0，1)点可求得该曲线斜率k，若测得分支管道内的流量，即可得到主管道内的流量q主=kq分.依据以上试验结论，即可采用小管道流量测量来计算出大管径液体流量.在小管径流量测量中，可以采用较为精确的流量测量装置，以提高大管径流量测量的精确度，同时小管径中应用的流量计价钱也比较便宜.所以，该方法可以提高测量精确度和提高经济性，可以在火力发电厂及工业生产的大管径液体流量测量中应用和推广.

［1］沈维道，蒋智敏，童钧耕.工程热力学［M］.北京:高等教育出版社，2002.

［2］张燕侠.流体力学泵与风机［M］.北京:中国电力出版社，2012.

［3］史秀丽，张宏峰，李文鹏，等.流量计量在工业上的应用及其重要性［J］.工业计量，2006(2):148-149.

［4］陈文义，张 伟.流体力学［M］.天津:天津大学出版社，2004.

［5］刘志昌.工程流体力学［M］.天津:天津科学技术出版社，1996.