单木生长模型与林分生长模型耦合的方法——以油松为例

高东启，邓华锋*，蒋 益，陈虹兵，程志楚

(1.北京林业大学 林学院，北京 100083;2.国家林业局调查规划设计院，北京 100714)

单木生长模型与林分生长模型各有特点，利用单木生长模型预测林分变量时，可以判定各单株木的生长状况和生长潜力，但是存在着误差积累、复杂性等缺点;通过林分生长模型预测林分变量时，可以直接提供林分的收获量，但却无法反映单木水平的详细信息［1-5］，且单木生长模型与林分生长模型预测的同一林分变量可能不一致［5-6］。因此，有必要对单木生长模型与林分生长模型进行整合，使两类模型能够有机的耦合，紧密地联系起来形成一个统一的整体，从而保证预测结果的一致。邓成等［6-7］提出了林分生长与收获模型的整体化研究思路，但是没有考虑抚育间伐等经营管理措施对林分生长的影响。

而现实的林分由于受抚育间伐等经营管理措施的影响，与自然生长的林分相比，其生长规律会发生变化［8］。在林分生长与收获预估模型的研究中，抚育间伐作为独立于林龄、立地质量、密度之外的第4 个建模因子越来越受研究者的重视［9］，相关学者已经研究了抚育间伐对落叶松、杉木、侧柏、马尾松等的影响［10-16］，而间伐措施对北京市油松(Pinus tabulaeformis)生长变化规律的影响还有待进一步研究。本文以油松林分断面积、蓄积量生长模型为例，在考虑林分间伐效应的基础上，研究单木生长模型与林分生长模型耦合的方法。

1 材料与方法

1.1 研究地概况

北京市位于北纬39°28'～41°05'，东经115°25'～117°30'，地处华北平原北端，北以燕山山地与内蒙古高原接壤，西以太行山与陕西高原毗连，东北与松辽平原相通，南与黄淮海平原连片;属于暖温带半湿润大陆性季风型特点，四季分明，夏季炎热多雨，冬季寒冷干燥，夏季降水量占全年降水量的74%。

1.2 数据来源与处理

本研究所采用的数据来源于国家林业局调查规划设计院，为国家一类清查数据，分别调查于1996、2001、2006 年，每个样地的面积为0.066 7 hm2。样地主要调查因子有:林木胸径、林分年龄、林分平均高、林分蓄积、枯损蓄积、采伐蓄积、郁闭度、水平距、坡向、坡位、坡度、海拔高度、土层厚度等，样地固定且每隔5 年复测1 次，调查期内部分林分进行了抚育间伐。

从收据的数据中共挑选出北京市油松人工林样地133 块，经过间伐的样地69 块，未经间伐的样地64 块。对133 块样地进行随机抽样，共有80 块样地用于建模，剩余53 块样地用于检验，统计样地基本情况如表1 所示，主要有林分的平均年龄、平均胸径(即平方平均胸径)、平均树高、优势木平均高、平均每公顷株数、每公顷断面积和每公顷蓄积。

油松样地资料中没有林分优势高，表1 中的林分优势高是通过林分优势高与林分平均高的关系计算出来的，参考贺姗姗［17］的研究结果，其通过解析优势木的方法，得到油松人工林优势高与林分平均高的相关关系为:H=1.115 h+0.429 3(H 为油松林分优势高，h 为油松林分平均高，决定系数为0.952 1)。通过上式计算出油松各样地的林分优势高，查询北京油松人工林的地位指数表［18］，作为评价林分立地质量的指标。

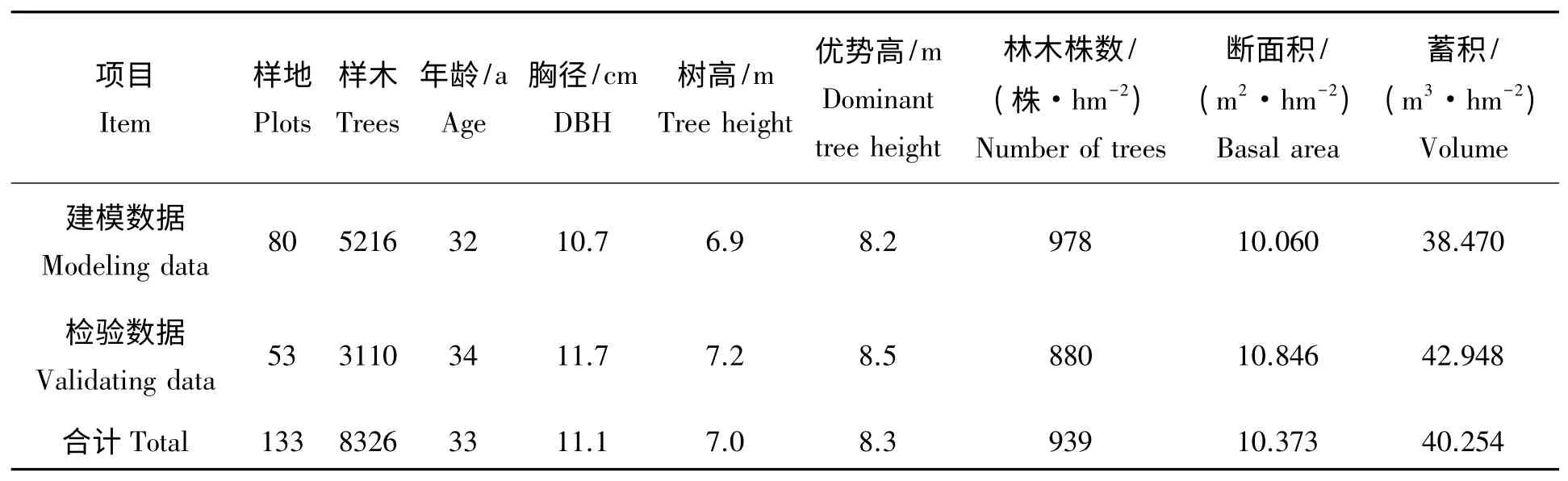
表1 样地基本情况Tab.1 The condition of plots

表2 统计了随机抽样的样地、样木分布情况，其中，在建模数据中，间伐林分有41 块样地、2 859株样木，未间伐林分有39 块样地、2 357株样木;在检验数据中，间伐林分有28 块样地、1 683株样木，未间伐林分有25 块样地、1 427株样木。

表2 样地、样木分布情况Tab.2 The distribution of plots and trees

1.3 研究方法

相关研究表明:通过单木生长模型推导林分生长模型的方法可以使得两类模型有机的耦合，该方法由邓成等［6-7］在林分生长与收获模型的整体化研究中提出，其核心是不同类型的模型之间的相关推导和变换，先寻找各个水平模型相互之间的关系，然后再进行变形和转换。但是邓成等没有考虑林分经营措施对林分生长的影响，下面采用单木生长模型推导林分生长模型的方法对两类模型进行耦合，并考虑间伐措施对油松林分断面积、蓄积量生长的影响，首先建立单木水平生长模型。

1.3.1 单木水平生长模型的研究 单木水平主要是建立油松单木断面积和材积生长模型，单木生长模型是地位指数(SI)、单木年龄(t)、林分密度和单木竞争指标等的函数［6-7，19］。以每公顷株数(N)作为反映林分密度的指标，单木竞争指标选用单木的相对直径Rd，选用Richards 方程研究单木断面积和材积生长模型，其基本形式如下:

式中，g 为单木断面积，v 为单木材积，SI 为地位指数，N 为每公顷株数，Rd为相对直径，t 为单木年龄，a1～a6为待定参数。

考虑到间伐林分与未间伐林分生长规律不同，因此通过在参数中引入哑变量的方法［20-21］，将油松间伐林分、未间伐林分分别用哑变量(即定性代码)来表示，从而可以将两种类型的林分合在一起建立统一的油松单木生长模型。经过初步试验，发现哑变量主要影响模型(1)、(2)式中的参数a1，即将哑变量引入参数a1中时，模型的模拟效果最好，因此确定含哑变量的单木生长模型的形式如下:

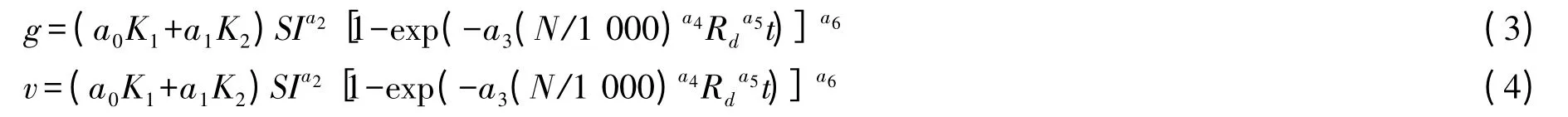
其中，g 为单木断面积，v 为单木材积，K1、K2(引入的哑变量)分别为间伐林分和未间伐林分的定性代码，SI 为地位指数，N 为每公顷株数，Rd为相对直径，t 为单木年龄，a0～a6为待定参数。

1.3.2 林分水平生长模型的研究 为了使得单木水平模型与林分水平模型能够有机地耦合，下面采用上面的单木断面积、材积生长模型(3)、(4)式分别推导林分断面积、蓄积量生长模型。

对于单木断面积、材积生长模型，当令(3)、(4)式中的相对直径Rd=1 时，即单木的胸径等于林分的平均胸径，此时就变成了林分平均标准木的断面积、材积生长模型。在模型(3)、(4)式中，由于Rd=1，因此参数a5可去除，保持其他参数的形式不变，得到含哑变量的林分平均标准木的断面积、材积生长模型为:

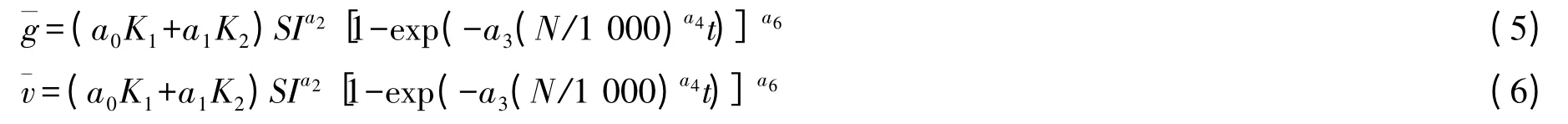
对于林分平均标准木的断面积、材积生长模型(5)、(6)式，再乘以林分株数n，就得到了含哑变量的林分断面积和蓄积量生长预估模型，具体过程如下:

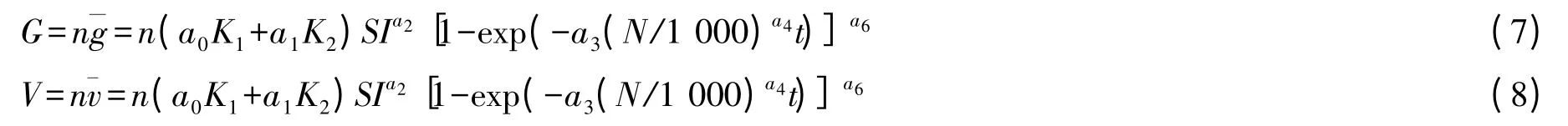
对于(7)、(8)式，为了使简化模型形式，减少模型中自变量的个数，进行如下的变换。林分每公顷株数N=n/0.066 7，则有林分株数n=0.066 7N，将其代入(7)、(8)式，得到最终的林分断面积、蓄积量生长预估模型，形式为:

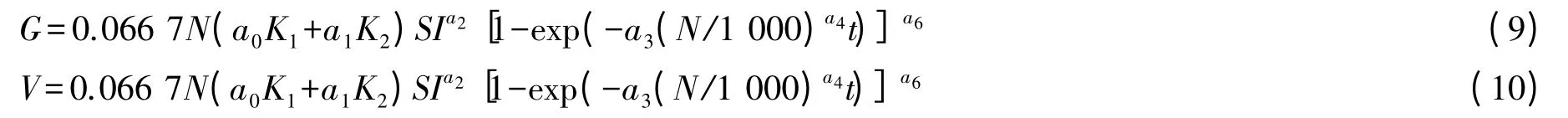
其中，G 为林分的断面积，V 为林分的蓄积量，K1、K2(引入的哑变量)分别为间伐林分和未间伐林分的定性代码，SI 为地位指数，N 为每公顷株数，t 为林分年龄，a0～a6为待定参数。

1.3.3 参数估计与模型检验 综合应用ForStat［22］、Excel、SPSS 进行数据计算和参数估计，并对模型进行t 检验，同时计算平均绝对偏差(MAD)、均方根误差(RMSE)、决定系数(R2)和预估精度(P%)等几个指标来检验模型的预测能力，它们的数学表达式如下:

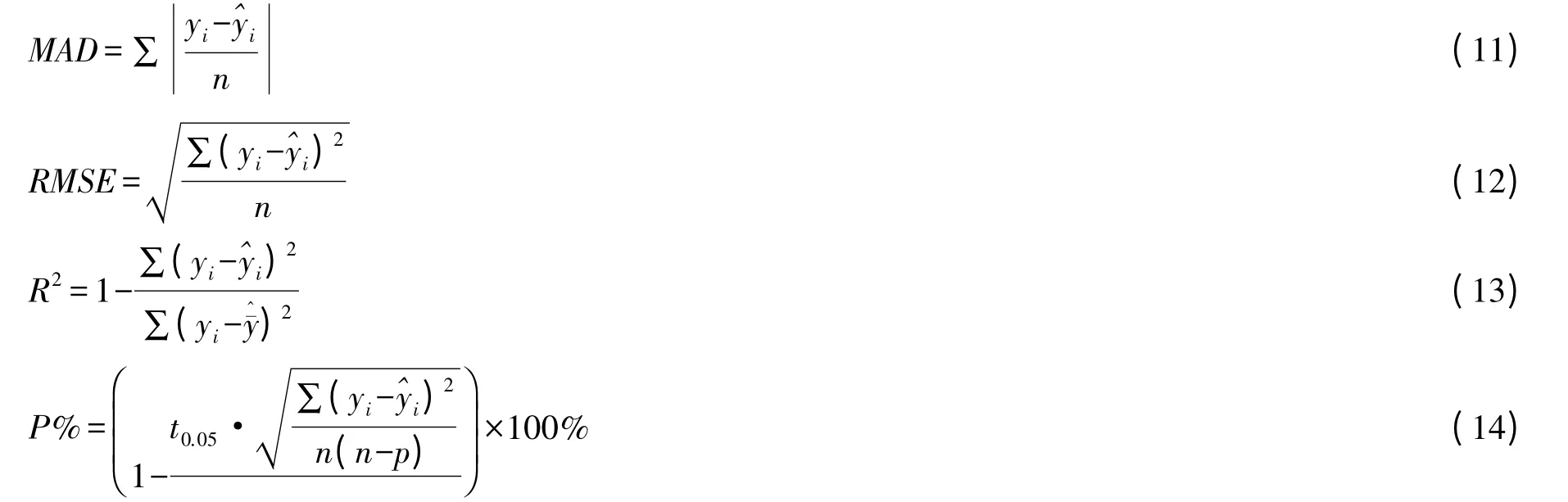
式中:yi为实测值(林分平均直径、林分平均高)为模型预估值为模型预估值的平均值，n 为样本数，p 为模型参数个数，t0.05为置信水平a=0.05 时的t 分布值。

2 结果与分析

对单木水平生长模型(3)、(4)式进行参数估计，统计油松单木断面积、材积生长模型参数a1～a6的估计值和R2如下表3 所示，其中油松单木断面积生长模型的决定系数为0.876 8，单木材积生长模型的决定系数为0.864 5，R2都较高，说明模拟效果较好。

表3 单木水平生长模型参数统计Tab.3 Parameter statistics of individual tree-level growth models

利用建模数据和检验数据对单木水平生长模型(3)、(4)式进行检验，统计平均绝对偏差(MAD)、均方根误差(RMSE)、决定系数(R2)、预估精度(P%)等指标如下表4 所示。单木断面积生长模型对建模数据的预测精度和R2分别为99.25%、0.876 8，对于检验数据的预测精度和R2分别为98.64%、0.787 1，MAD 和RMSE 等误差都较小，不超过0.005;单木材积生长模型对建模数据的预测精度和R2分别为99.03%、0.864 5，对于检验数据的预测精度和R2分别为98.41%、0.777 2，MAD 和RMSE 均小于0.021，误差较小，说明模型预测效果很好。进行t 检验，结果为Sig.＜0.05，说明实测值与预测值在0.05 的显著水平上无显著差异，模型建立的比较合理。

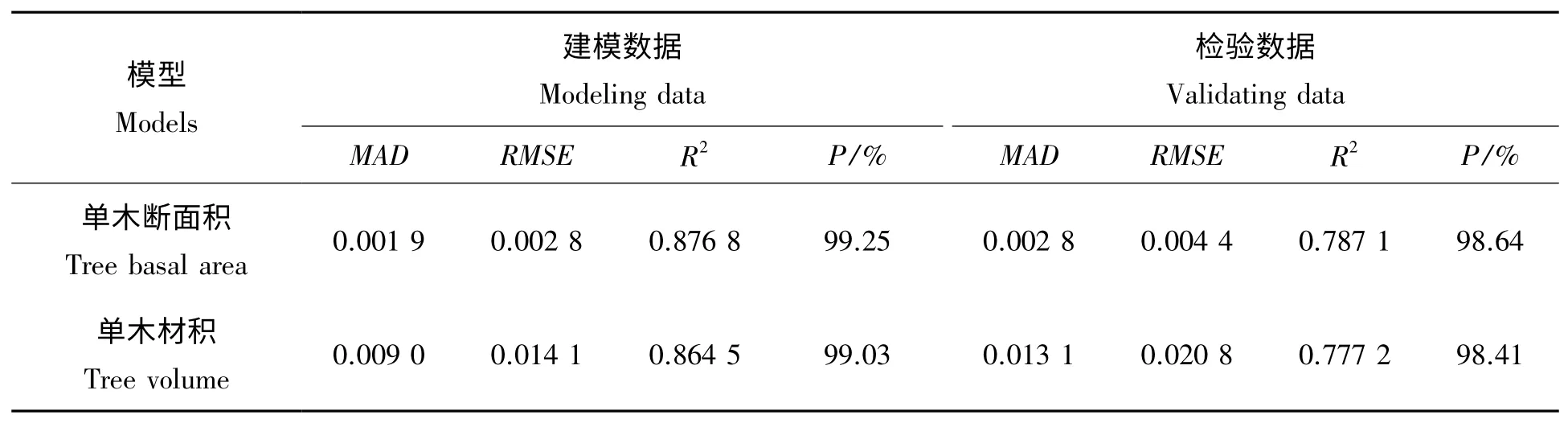
表4 单木水平生长模型检验Tab.4 Inspection of individual tree-level growth models

进一步检验单木生长模型(3)、(4)式对间伐林分和未间伐林分的预测效果，统计相关结果如下表5 所示。单木模型对间伐林分单木断面积的预测精度和R2分别为98.77%、0.885 8，MAD 为0.002 1，RMSE 为0.003 1;对间伐林分单木材积的预测精度和R2分别为98.55%、0.881 1，MAD 为0.009 9，RMSE为0.014 7。单木模型对未间伐林分单木断面积的预测精度和R2分别为97.22%、0.700 3，MAD 为0.003 6，RMSE 为0.005 6;对材积的预测精度和R2分别为96.74%、0.680 6，MAD 为0.016 9，RMSE 为0.026 3。单木模型对间伐林分和未间伐林分的预测精度都在96%以上，各项误差均较小，说明所建哑变量模型比较合理。t 检验结果都为Sig.＜0.05，即实测值与预测值在0.05的显著水平上无显著差异。

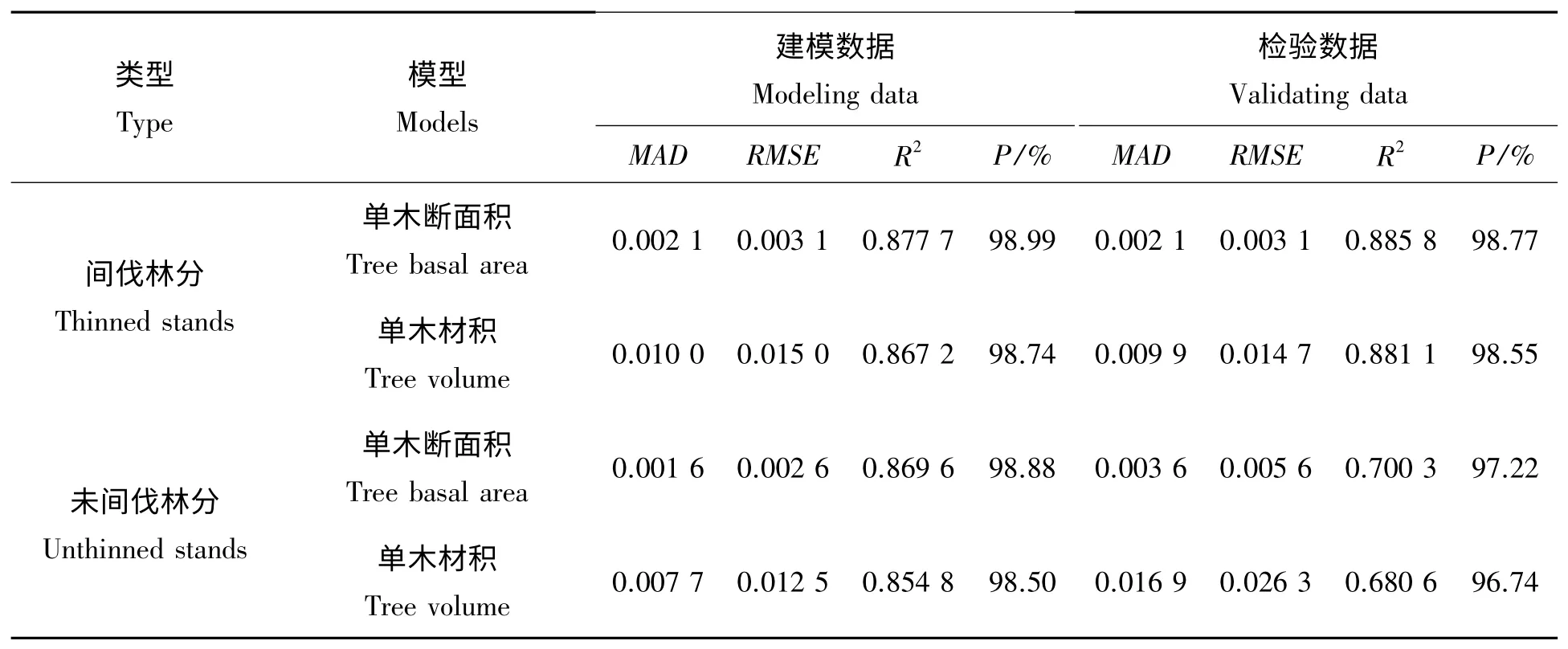
表5 间伐林分和未间伐林分单木生长模型预测结果检验Tab.5 Inspectiing forecast results of tree growth models for thinned stands and unthinned stands

由于林分水平生长模型(9)、(10)式是通过单木水平生长模型(3)、(4)式推导而来的，因此将相关的参数a1～a6(表3)带入(9)、(10)式得到林分水平生长模型(11)、(12)式:

利用建模数据和检验数据对林分水平生长模型(15)式、(16)式进行检验，结果如下表6 所示。对于建模数据而言，林分断面积生长模型的预测精度和R2分别为94.17%、0.848 5，MAD 为0.124 8，RMSE为0.167 9;林分蓄积量生长模型的预测精度和R2分别为92.60%、0.806 5，MAD 为0.586 8，RMSE 为0.810 0。对于检验数据而言，林分断面积生长模型的预测精度和R2分别为88.59%、0.763 4，MAD 为0.165 0，RMSE 为0.273 2;林分蓄积量生长模型的预测精度和R2分别为86.44%、0.711 9，MAD 为0.775 8，RMSE 为1.280 1。通过检验，林分断面积、蓄积量生长模型的预估精度较高超过了86%，误差较小，t 检验结果为Sig.＜0.05，说明实测值与预测值无显著差异，模型比较合理，含哑变量的林分模型使得油松间伐林分与未间伐林分能够相容从而合到一起。

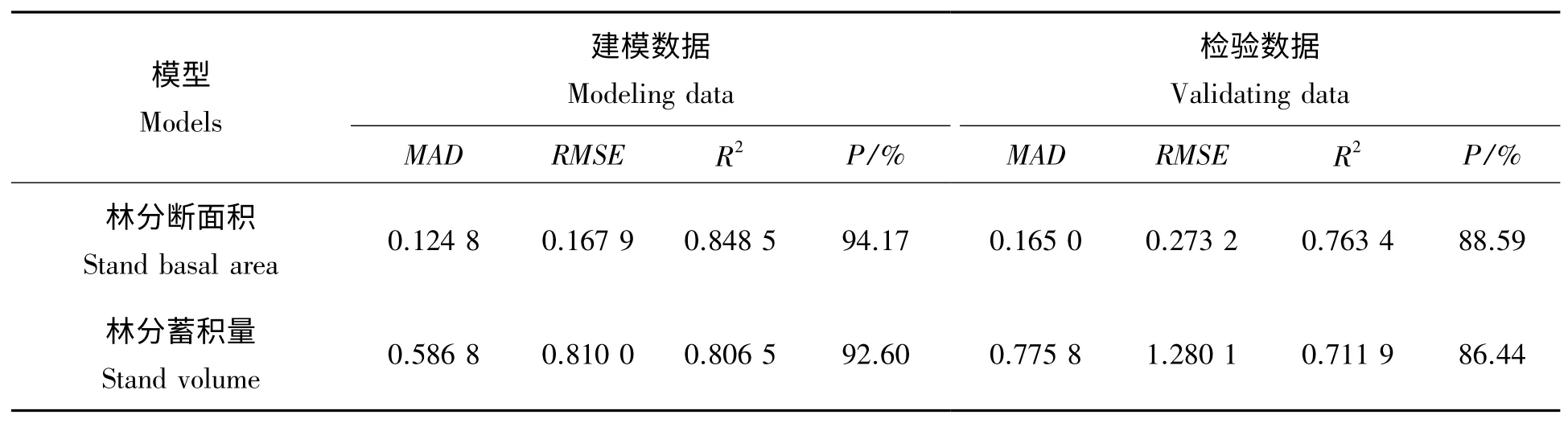
表6 林分水平生长模型检验Tab.6 Inspection of stand-level growth models

进一步检验林分生长模型(15)、(16)式对间伐林分和未间伐林分的预测效果，结果如下表7 所示。林分模型对间伐林分断面积的预测精度和R2分别为90.68%、0.832 0，对间伐林分蓄积量的预测精度和R2分别为89.08%、0.799 2;林分模型对未间伐林分断面积的预测精度和R2分别为87.01%、0.793 0，对未间伐林分蓄积量的预测精度和R2分别为85.90%、0.739 8，模型对间伐林分的预测效果要稍微好于未间伐林分。进行t 检验，结果为Sig.＜0.05，说明实测值与预测值在0.05 的显著水平上无显著差异;同时林分模型对间伐林分和未间伐林分的预测精度都在85%以上，说明所建哑变量模型比较合理，预测效果较好。

表7 间伐林分和未间伐林分生长模型预测结果检验Tab.7 Inspectiing forecast results of stands growth models for thinned stands and unthinned stands

3 结论与讨论

本文在考虑林分间伐效应的基础上，引入哑变量将间伐林分与未间伐林分整合到一起建立统一的单木断面积、材积生长模型，进一步对模型进行变换推导出林分生长模型，从而使得单木、林分两个水平的模型能够有机的耦合，形成一个联系紧密的整体，使模型更具有生物学意义和可解释性。

所建单木模型对油松单木断面积、材积的预测精度在98%以上，对间伐林分、未间伐林分的预测精度都在96%以上;而推导出的林分模型对油松林分断面积、蓄积量的预测精度分别为88.59%、86.44%，对间伐林分、未间伐林分的预测精度都在85%以上。模型对林分蓄积量的预测精度稍低于林分断面积，可能的原因是林分蓄积量由林分中各单木的材积推算而来，而单木材积并非实测值，而是由北京市一元立木材积表所得，存在一定的误差，所以预测精度稍低。

单木生长模型推导林分生长模型的方法，使得两个水平的模型能够整合在一起，并保证了两个水平模型对林分断面积、蓄积量预测精度的一致，该方法不仅适用于预测林分断面积、蓄积量，也适用于预测其他林分因子。本文所用数据调查时间不同，没有考虑时间效应对建模的影响，下步可建立混合模型进行更深入的研究。

本文所建模型对北京地区的油松人工林是适用的，可以用来模拟其单木或林分的生长，从而为油松林分的经营管理决策提供参考依据。

［1］赵俊卉.长白山云冷杉混交林生长模型的研究［D］.北京:北京林业大学，2010.

［2］孟宪宇.测树学［M］.3 版.北京:中国林业出版社，2008.

［3］Qin J，Cao Q V.Using disaggregation to link individual-tree and whole-stand growth models［J］.Canadian Journal of Forest Research，2006，36(4):953-960.

［4］张雄清，雷渊才，陈新美，等.组合预测法在林分断面积生长预估中的应用［J］.北京林业大学学报，2010，32(4):6-11.

［5］胡焕香，佘济云，李俊，等.湖北桂花林场檫木次生林单木生长模型的研究［J］.中南林业科技大学学报，2013，33(4):61-65.

［6］邓成.林分生长和收获模型整体化研究［D］.长沙:中南林业科技大学，2008.

［7］邓成，吕勇，雷渊才，等.林分生长和收获模型整体化思路探讨［J］.林业调查规划，2008，33(4):7-9.

［8］谢华.杉木人工林抚育间伐效应研究［D］.合肥:安徽农业大学，2007.

［9］Sun H G，Zhang J G，Duan A G，et al.A review of stand basal area growth models［J］.Forestry Studies in China，2007，9(1):85-94.

［10］毕永华.兴安落叶松林不同间伐强度林分生长模型的研究［D］.哈尔滨:东北林业大学，2001.

［11］雷相东，陆元昌，张会儒，等.抚育间伐对落叶松云冷杉混交林的影响［J］.林业科学，2005，41(4):78-85.

［12］李春明，杜纪山，张会儒.间伐林分的断面积生长模型研究［J］.林业资源管理，2004(3):52-55.

［13］李春明，杜纪山，张会儒.抚育间伐对人工落叶松断面积和蓄积生长的影响［J］.林业资源管理，2007(3):90-93.

［14］段劼，马履一，贾黎明，等.抚育间伐对侧柏人工林及林下植被生长的影响［J］.生态学报，2010，30(6):1431-1441.

［15］明安刚，张治军，谌红辉，等.抚育间伐对马尾松人工林生物量与碳贮量的影响［J］.林业科学，2013，49(10):1-6.

［16］赵西哲.湘中南地区主要用材林森林抚育综合效益研究［D］.长沙:中南林业科技大学，2007.

［17］贺珊珊.北京山区油松人工林林分结构与生长结构研究［D］.北京:北京林业大学，2009.

［18］段劼，马履一，贾黎明，等.北京低山地区油松人工林立地指数表的编制及应用［J］.林业科学，2009，45(3):7-12.

［19］郎荣，许建初，Timm Tennigkeit，等.基于样方数据的云南松林分生长模型研究—以云南省保山市杨柳白族彝族乡为例［J］.植物分类与资源学报，2011，33(3):357-363.

［20］李忠国，孙晓梅，陈东升，等.基于哑变量的日本落叶松生长模型研究［J］.西北农林科技大学学报，2011，39(8):69-74.

［21］高东启，邓华锋，王海宾，等.基于哑变量的蒙古栎林分生长模型研究［J］.东北林业大学学报，2014，42(1):61-64.

［22］唐守正，郎奎建，李海奎.统计与生物数学模型计算(ForStat 教程)［M］.北京:科学出版社，2009.