中国夏季降水异常EOF模态的时间稳定性分析
庞轶舒 祝从文 刘凯
中国气象科学研究院,北京100081
1 引言
经验正交分解(Empirical orthogonal function,EOF)又被称为主成分分析(Principal component analysis,PCA),最早由Pearson提出(Pearson,1902),20世纪50年代Lorenz将该方法引入大气科学领域(Lorenz,1956),随后被广泛应用至今。EOF方法的优点在于它能对分布不规则的气象要素场进行时空分解,得到的各特征向量(空间模态和时间系数)相互正交,其中空间模态(EOF)在一定程度上可反映要素场的空间分布特点,而时间系数(PC)则反映相应空间模态随时间的权重变化。除此之外,EOF方法还具有展开收敛速度快,容易将原始要素场的变化信息浓缩在前几个模态上的特点。因此,该方法常用于气象要素场时空变化特征规律研究。
EOF方法是气候研究中的主要方法之一,在过去几十年,中国学者利用该方法对中国降水时空变化特征做了大量研究(例如,王绍武和赵宗慈,1979;邓爱军等,1989;李栋梁等,1997;宋正山和杨辉,2001;魏凤英,2003;孙林海等,2005;Wang et al.,2013;封国林等,2013 ;Zhang et al., 2013)。其中,王绍武和赵宗慈(1979)利用此方法分析了我国旱涝分布特点,并在此基础上提出了中国6种主要雨型的观点。宋正山和杨辉(2001)利用此方法分析了500 hPa环流场与我国夏季降水(雨型)相关分布,指出该环流场前两个模态与中国夏季降水主要分布型有很好的对应关系。除此之外,学者们还将EOF方法应用于短期气候和区域统计降尺度预测中,通过EOF各模态的PC系数预测和重建来预测未来要素场的变化(章基嘉等,1979;Harnack and Lanzante, 1985;袁景凤和吴晓曦,2000;何慧等,2004)。例如,何慧等(2004)通过对广西前汛期降水距平百分率作 EOF 分解,选取累积方差贡献接近70%的前五个模态为预报量,利用统计方法建立降水预报模型。众所周知,在EOF重建过程中,参与模态越多,重建场与原始场越接近。然而,在利用EOF方法预测时,参与模态的选取则有严格的条件限制。章基嘉等(1981)指出,只有EOF模态在预测时效内稳定,该模态的信息才可用于未来的气候预测。Charles et al.(1999)、Wilby and Wigley(2000)指出预报因子和预测函数随时间稳定是建立统计预测模型的基本条件。因此,在利用 EOF方法建立气候预测模型时,需首先讨论各EOF模态是否随时间发生变化。为方便讨论,本文将 EOF模态不随时间发生变化称作时间稳定。
夏季降水一直是我国短期气候预测的重点内容,近年来许多气象工作者在前人研究的基础上提出了新的预测方法及思路并取得了不错的预测效果(郭玲,2011;郭彦和李建平,2012;Liu and Fan,2012),但就现阶段而言,全国范围的降水预测水平还有待进一步提高。而研究中国夏季降水 EOF模态的时间稳定性对于认识中国夏季降水主要变化特征,并从降水全局变化角度探索可能的预测方法具有重要的意义。因此,本文分析和讨论了1980~2012年中国夏季降水距平和距平百分率前四个EOF模态的特征和时间稳定性,在此基础上探讨 EOF方法在整个中国地区夏季降水预测中的潜在能力和应用条件。
2 资料和分析方法
本文采用的资料为中国气象局信息中心提供的1951~2012年全国160台站夏季(6~8月)逐月降水资料,该套资料常用于国家气候中心的短期气候预测工作。研究过程中,本文首先对 1980~2012年降水距平和距平百分率进行EOF分解,取前四个模态进行分析。在此基础上,利用滑动交叉检验、独立样本检验、距平相关系数(Anomaly correlation coefficient,ACC)、时间相关系数(Temporal correlation coefficient,TCC)等方法讨论EOF各模态的时间稳定性。为定量评估EOF各模态的时间稳定性,本文定义了时间稳定性指数(Stability Index, SI),即资料时间长度处理前后对应空间模态ACC和时间系数TCC的乘积,并将稳定标准设为 0.5。其中,资料时间长度处理分别通过滑动交叉检验[见公式(1)]和独立样本检验[见公式(2)]两种方法实现。
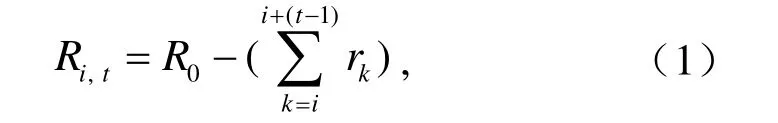
其中,Ri,t为时间长度处理后的资料(i=1980,1981,…,2012;t为剔除时间长度:1,2,3,4,5);R0为原始资料(1980~2012年夏季降水场);r为样本元素。

其中,Ri为时间长度处理后的资料(i=2003,2004,…,2012);R0为原始资料(1980~2002年夏季降水场);r为样本元素。
3 中国夏季降水异常主要模态的特征分析
过去很多研究认为中国东西部降水气候特点不同(徐国昌,1997;孙国武,1997;朱乾根等,2007),基于这种观点,对整个中国地区夏季降水进行EOF分析很可能无法区分东西部降水的特征。为此,我们对比了 1980~2012年中国和中国东部地区(100°E以东)夏季降水距平、距平百分率的前四个EOF模态。对比结果表明,两者夏季降水距平各模态的解释方差差异较小,对应空间分布形态相似,PC系数变化一致,相关系数接近1.0(图略)。而两者降水距平百分率各模态的差异则主要表现在前两个模态的顺序发生了对调,其对应PC系数的时间相关关系仍然通过显著性水平为 0.01的检验。由此可见,尽管中国东西部地区降水特性有所差异,但由于EOF分析结果突出的是降水方差贡献较大的区域,所以从整体角度进行EOF分析不仅能很好地反映方差贡献较大的东部降水特征,同时也能反映西部地区降水的一些特性,适用于全国夏季降水预测。
基于上述讨论,本文重点分析中国夏季降水距平和距平百分率的前四个EOF模态。图1表示降水距平前四个EOF模态的空间分布特征,其中,各模态的解释方差分别为 18.45%、10.93%、8.14%和7.44%,累计方差贡献约 45%。如图所示,第一模态在100°E以东地区表现出南北向“+、-、+”的三极型分布,是东亚夏季风降水的主要空间分布型;第二模态表现出以长江为界,南北方降水反相变化的特征;第三模态表现为江南地区、东北部分地区和西北地区降水偏少,其余地区降水偏多的特征;第四模态则呈现华南、黄淮区域降水偏少,其他区域降水偏多的特征。而从降水距平百分率前四个EOF模态分析结果(图2)可以看出,其各模态的解释方差依次是 14.46%、10.64%、7.95%和6.39%,累计方差贡献为39.44%。其中第一模态的空间分布表现为黄河以北地区与其余地区降水反向变化的特征;第二模态则呈现出南北向“-、+、-”三极型分布特征;第三模态表现为河套地区、华南沿海地区和其余地区降水反向变化特征;第四模态则表现为全国大部分地区降水偏多,零星地区降水偏少的特征。
从上述分析可以发现,作为指示降水异常的两种物理量,降水距平和距平百分率前四个模态的空间分布表现出多样性和复杂性,且各模态所占的方差贡献率最大不超过20%,这说明中国夏季降水的年际变化特征多样而复杂,单个EOF模态反映的信息十分有限,因此在利用EOF方法预测中国夏季降水时,必须尽可能考虑多个模态的信息。另外,由于降水距平和距平百分率侧重不同,前者反映降水偏离气候值的大小,后者反映降水偏离气候值的程度,所以两者各模态的空间分布差异明显。这说明在利用 EOF方法预测中国夏季降水时,这两种物理量不能相互替代。
4 中国夏季降水异常主要模态的时间稳定性分析
如前所述,时间稳定是各EOF模态应用到气候预测中的重要前提条件。为此,本文首先通过滑动交叉检验方法讨论中国夏季降水距平和距平百分率前四个模态的时间稳定性,以探究各EOF模态是否可参与中国夏季降水预测。
图3表示通过滑动交叉检验得到的中国夏季降水距平各EOF模态SI随时间和剔除时间长度(t)的变化情况,如图所示,当t≤5时,第一个模态的SI恒大于 0.9,高度稳定。第二模态在t=1时,SI恒大于0.8,高度稳定;在t=2时,SI在个别年份(如1998年)略低于稳定度标准0.5,其余年份高于0.8,基本稳定;在t>2时,SI的时间波动幅度增大,低于稳定标准的年份增多,时间稳定性下降。第三、四模态在t=1时,除个别年份(2008年)外,SI总体高于稳定性标准,基本稳定;在t>1时,SI波动幅度随t增加而增大,数值明显下降。由此可见,在利用EOF方法预测中国夏季降水距平时,随着预测时效增加,可参与预测的模态减少。当预测时效为一年时,前四个模态稳定,可参与未来气候预测;当预测时效为两年时,前两个模态基本稳定,可参与预测;当预测时效大于两年,仅第一模态的稳定性满足参与预测条件。
与降水距平相比,2012年在降水距平百分率各模态 SI随时间和剔除时间长度(t)的变化中表现出显著异常(见图4)。当被剔除资料包含2012年时,各模态 SI急剧下降。如果忽略 2012年的影响,则前两个EOF模态的SI始终高于0.5;第三模态的SI在t≤3时高于0.5,在t=4、5时除1994年
略低于0.5,其余高于0.5。而第四模态的SI波动较大,低于0.5的年份较多,稳定性较差。由此可见,在利用 EOF方法预测中国夏季降水距平百分率时,第四模态的稳定性较低,无法参与预测。另外,基于2012年之前的EOF模态特征无法准确预测该年的降水距平百分率。

图1 1980~2012年中国夏季降水距平场前四个EOF模态空间分布:(a)EOF-1;(b)EOF-2;(c)EOF-3;(d)EOF-4Fig. 1 The first four EOF modes of China summer precipitation anomalies during 1980–2012: (a) EOF-1; (b) EOF-2; (c) EOF-3; (d) EOF-4

图2 同图1,但表示的是距平百分率场Fig. 2 Same as Fig. 1, but for the field of precipitation anomaly percentage
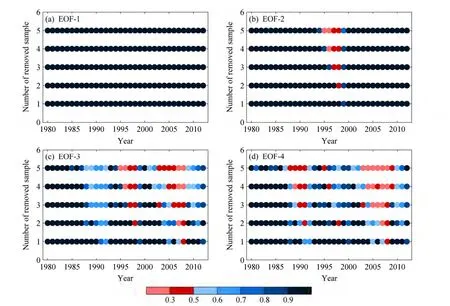
图3 1980~2012年中国夏季降水距平场前四个EOF模态稳定度(SI)随时间和剔除时间长度的变化:(a)EOF-1;(b)EOF-2;(c)EOF-3;(d)EOF-4Fig. 3 Stability indices of the first four EOF modes of China summer precipitation anomaly during 1980–2012, and their change with time and length of excluded time: (a) EOF-1; (b) EOF-2; (c) EOF-3; (d) EOF-4
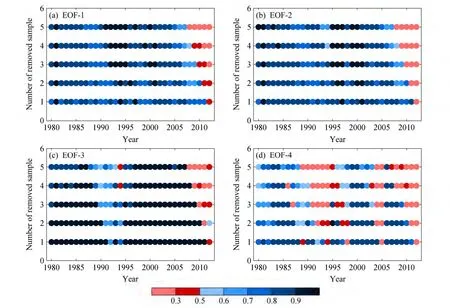
图4 同图3,但表示的是距平百分率场Fig. 4 Same as Fig. 3, but for the field of precipitation anomaly percentage
虽然滑动交叉检验结果在一定程度上反映了各模态的时间稳定性,但在实际预测时不知道未来的情况,预测结果仍然存在较大的不确定性。为此,我们通过独立样本检验方法进一步检验了降水距平和距平百分率前四个EOF模态在近10年的时间稳定性。结果表明,近 10年内中国夏季降水距平前三个模态的SI均大于0.9,表现出高度的稳定性;第四模态的SI在近10年内波动相对较大,尽管如此,其SI仅有一年(2007年)低于稳定度标准(图略)。而中国夏季降水距平百分率第一、四模态的SI在近10年中均大于或等于0.9,第二、三模态的SI除在2012年低于0.5,其余均大于0.8。总体而言,中国夏季降水距平和距平百分率前四个模态在近 10年中基本稳定。然而与滑动交叉检验结果类似,降水距平百分率前四个模态的时间稳定性在2012年相对较低。
5 极端降水事件对 EOF模态时间稳定性的影响
由于 EOF特征向量取决于样本资料的协方差矩阵,因此某一年的极端降水气候事件可能会对多年降水(距平和距平百分率)的EOF模态时间稳定性产生影响。2012年中国北方一些地区出现极端降水事件,以北京“7.21”大暴雨为例,全市日平均降水量达 170 mm,其中房山区高达 460 mm(http://www.cma.gov.cn/2011xwzx/2011xmtjj/201207/t20120724_179464.html)。因此,降水距平百分率各模态时间稳定性在 2012年的特殊性很可能由极端降水引起。
为验证极端降水气候事件对中国夏季降水EOF模态稳定性的影响,本文将1951~2012年中国160台站夏季降水(R)进行阈值修订(见公式3)以削弱极端降水的强度。经检验,该修订方法不会破坏原始降水的变化趋势和其降水距平(距平百分率)各 EOF模态的基本特征(图略)。在此基础上,对比阈值修订前后降水距平和距平百分率前四个模态SI的滑动交叉检验结果。
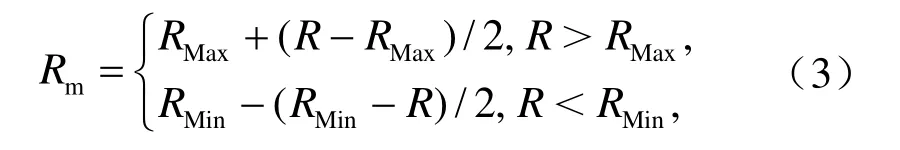
其中,Rm为修订后的降水资料,RMin和RMax则被定义为1951~2012年各站点降水序列(由低到高)5%和95%分位数的值。
通过对比修订前后降水距平各模态的 SI(图5)可以发现,当t≤5时,前四个模态的 SI在大多数年份中减小,在少数年份中增加,差异值小于 0.3,改变幅度不大。但比较特殊的是,当t=2时,第三、四模态的SI在一些年份中下降程度大于0.5。
与降水距平不同,降水距平百分率第一、二、四模态的SI在阈值修订前后总体提高(图6),尤其当剔除资料中含2012年时第一模态(t≤5)和第二模态(t≤2)SI的增加值超过0.5。而其第三模态SI的下降年份数偏多,但改变幅度不大。阈值修订后,距平百分率各模态 SI随时间和剔除时间长度(t)的变化如图7所示,当t≤5时,其第一模态的SI恒大于0.8,高度稳定。而第二、三模态的SI在t=1时大于0.6,基本稳定;在t>1时,低于0.5的年份数增多,稳定性较差。而第四模态SI在t≤5时波动明显,低于0.5的年份较多,稳定性较差。
从以上分析可以看出,阈值修订方法对降水距平百分率各模态 SI有明显改善作用,消除了其在2012年的特殊性,而对降水距平各模态SI的改善作用则不明显。这说明,与降水距平相比,降水距平百分率各模态的时间稳定性更易受到极端降水的影响。然而极端降水的产生不仅受到气候变化的影响,天气尺度和中小尺度气象条件变化的影响也十分重要,但在短期气候预测中,天气尺度和中小尺度的气象要素变化无法准确预测。因此在利用EOF方法预测中国夏季降水距平百分率时,可首先对降水资料进行阈值修订。修订后,当预测时效为1年时,前三个模态可参加预测;当预测时效为 1年以上时,仅第一模态可参加预测。
综合第4、5节研究结果可以发现,当利用EOF方法预测未来一年中国夏季降水时,可参与预测的模态最多,即降水距平前四个模态或修订后降水距平百分率前三个模态。假设各模态PC系数预测完全准确,则可以通过它们的EOF重建场与原始场的TCC和ACC来讨论EOF方法的潜在预测能力。研究结果表明(图略),降水距平前四个模态能解释原始降水 45%的变化方差,其重建场与原始场的TCC显著相关(α=0.05)站点集中分布在黄河以南大部分地区,平均ACC约为0.6。而修订后降水距平百分率前三个模态能解释原始降水 30.74%的变化方差,其重建场与原始场的 TCC显著相关(α=0.05)站点分布在中国大部分地区,平均 ACC为0.48。由此可见,EOF方法在中国夏季降水年际变化预测中有一定潜力,当以降水距平百分率为预测对象时,可预测范围相对较大,当以降水距平为预测对象时,预测结果相对准确。
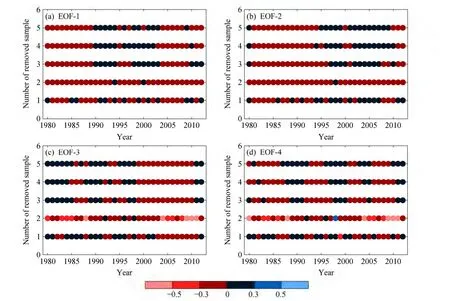
图5 1980~2012年阈值修订前后中国夏季降水距平场EOF模态的稳定度(SI)差异(后者减前者):(a)EOF-1;(b)EOF-2;(c)EOF-3;(d)EOF-4Fig. 5 Differences of stability indices between the original and modified Chinasummer precipitation anomalies for the first four EOF modes during 1980–2012: (a) EOF-1; (b) EOF-2; (c) EOF-3; (d) EOF-4
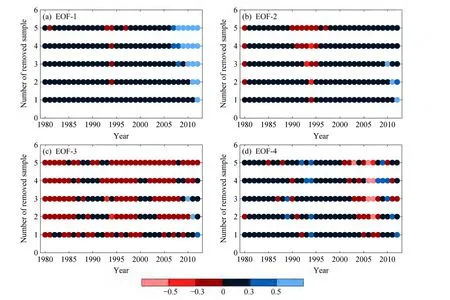
图6 同图5,表示的是距平百分率场Fig. 6 Same as Fig. 5, but for the precipitation anomaly percentage

图7 阈值修订后1980~2012年中国夏季降水距平百分率场前四个EOF模态稳定度(SI)随时间和剔除时间长度的变化:(a)EOF-1;(b)EOF-2;(c)EOF-3;(d)EOF-4Fig. 7 Stability indices of the first four EOF modes of the modified China summer precipitation anomaly percentage during 1980–2012, and their change with time and length of excluded time: (a) EOF-1; (b) EOF-2; (c) EOF-3; (d) EOF-4
6 结论和讨论
本文基于1980~2012年中国160个台站夏季降水资料,分析和研究了降水距平与距平百分率前四个EOF模态的特征和时间稳定性,讨论了极端降水事件对各模态时间稳定性的影响,并提出了一种通过削弱极端降水强度来提高降水距平百分率各模态时间稳定性的方法。在此基础上,探讨了EOF方法在中国夏季降水短期气候预测中的潜在能力。
研究发现,中国夏季降水距平第一模态在预测时效为5年内时间稳定,第二模态在2年内时间稳定,第三、四模态在1年内时间稳定。而受极端降水事件影响,中国夏季降水距平百分率各模态时间稳定性较低,无法参与预测。当对资料进行阈值修订,人为削弱极端降水影响后,距平百分率前三个模态的时间稳定性显著提高,其中第一模态在预测时效为5年内时间稳定,第二、三模态在1年内时间稳定。因此,可以利用降水距平前四个EOF模态或修订后降水距平百分率前三个 EOF模态的信息预测未来一年中国夏季降水的变化。假设PC系数预测完全准确,降水距平前四个模态可以解释原始降水 45%的变化方差,其重建场与原始场的 TCC显著相关站点集中分布在黄河以南地区,平均ACC约为 0.6。而修订后降水距平百分率前三个模态能解释原始降水 30.74%的变化方差,其重建场与原始场的 TCC显著相关站点在全国均匀分布,平均ACC为0.48。相较而言,在利用EOF方法预测中国夏季降水时,距平比距平百分率更适合作预测对象。
本文主要讨论了 EOF方法在中国夏季降水短期气候预测中的潜在应用价值。但在实际预测之前,我们还需要进一步探索各模态PC系数的影响因子以及多因子配置与各模态PC之间的关系,以建立中国夏季降水预测模型。此外,新研究表明在降水预测中以年际增量作为预测对象能取得不错的预测结果(范可等,2007),因而通过年际增量讨论 EOF方法的潜在预测能力亦十分重要。这两个问题将是作者今后研究的重要内容。
References)
Charles S P, Bates B C, Whetton P H, et al. 1999. Validation of downscaling models for changed climate conditions: Case study of southwestern Australia [J]. Climate Research, 12: 1–14.
邓爱军, 陶诗言, 陈烈庭. 1989. 我国汛期降水的EOF分析 [J]. 大气科学, 13 (3): 289–294. Deng Aijun, Tao Shiyan, Chen Lieting. 1989. The EOF analysis of rainfall in China during monsoon season [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 13 (3): 289–294.
范可, 王会军, Young-Jean C. 2007. 一个长江中下游夏季降水的物理统计预测模型 [J]. 科学通报, 52 (24): 2900–2905. Fan Ke, Wang Huijun, Young-Jean C. 2007. A physical-statistical prediction model for summer rainfall in the middle and lower reaches of the Yangtze River [J].Chinese Science Bulletin (in Chinese), 52 (24): 2900–2905.
封国林, 孙树鹏, 赵俊虎, 等. 2013. 基于 2009年初长江中下游地区持续阴雨过程的10~30天延伸期稳定分量的提取及配置分析 [J]. 中国科学: 地球科学, 43 (5): 836–847. Feng Guolin, Sun Shupeng, Zhao Junhu, et al. 2013. Analysis of stable components for extended-range(10–30 days) weather forecast: A case study of continuous overcast-rainy process in early 2009 over the mid-lower reaches of the Yangtze River [J].Science China: Earth Sciences. 56 (9): 1576–1587.
郭玲. 2011. 中国夏季降水影响因子评估和统计预测研究 [D]. 南京信息工程大学硕士学位论文. Guo Ling. 2011. Potential predictors evaluations and statistical prediction of summer rainfall in China [D]. M.S. thesis (in Chinese), Nanjing University of Information Science and Technology.
郭彦, 李建平. 2012. 一种分离时间尺度的统计降尺度模型的建立和应用——以华北汛期降水为例 [J]. 大气科学, 36 (2): 385–396. Guo Yan, Li Jianping. 2012. A time-scale decomposition statistical downscaling model: Case study of North China rainfall in rainy season[J]. Chinese Journal of Atmospheric Sciences (in Chinese), 36 (2): 385–396.
Harnack R P, Lanzante J R. 1985. Specification of United States seasonal precipitation [J]. Mon. Wea. Rev., 113: 319–325.
李栋梁, 谢金南, 王文. 1997. 中国西北夏季降水特征及其异常研究 [J].大气科学, 21 (3): 331–340. Li Dongliang, Xie Jinnan, Wang Wen.1997. A study of summer precipitation features and anomaly in northwest China [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 21 (3):331–340.
Lorenz E N. 1956. Empirical orthogonal functions and statistical weather prediction [R]. Science Report 1, Statistical Forecasting Project,Department of Meteorology, MIT (NTIS AD 110268), 49 PP.
Liu Y, Fan K. 2012. A new statistical downscaling model for autumn precipitation in China [J]. International Journal of Climatology, 33 (6):1321–1336.
何慧, 金龙, 覃志年. 2004. 降维方法在广西前汛期降水预测中的应用[J]. 灾害学, 19 (4): 7–12. He Hui, Jin Long, Qin Zhinian. 2004. The application of EOF method to the precipitation forecast during the first raining season in Guangxi [J]. Journal of Catastrophology (in Chinese),19 (4): 7–12.
Pearson K. 1902. On lines and planes of closest fit to systems of points in space [J]. Philos. Mag., 2 (6): 559–572.
宋正山, 杨辉. 2001. 夏季东亚季风区500 hPa月环流异常及与我国降水关系的向量 EOF分析 [J]. 大气科学, 25 (3): 401–410. Song Zhengshan, Yang Hui. 2001. Vector EOF expansion of summer monthly anomalous wind fields at 500 hPa over East Asia relation to rainfall over China [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 25 (3):401–410.
孙国武. 1997. 中国西北干旱气候研究 [M]. 北京: 气象出版社, 384.Sun Guowu. 1997. Research of Arid Climate in Northwest China (in Chinese) [M]. Beijing: China Meteorological Press, 384.
孙林海, 赵振国, 许力, 等. 2005. 中国东部季风区夏季雨型的划分及其环流成因分析 [J]. 应用气象学报, 16 (增刊): 56–62. Sun Linhai,Zhao Zhenguo, Xu Li, et al. 2005. Study of summer rain pattern in monsoon region of East China and its circulation cause [J]. Journal of Applied Meteorological Science (in Chinese), 16 (S1): 56–62.
王绍武, 赵宗慈. 1979. 近五百年我国旱涝史料的分析 [J]. 地理学报,34 (4): 329–341. Wang Shaowu, Zhao Zongci. 1979. An analyses of historical data of droughts and floods in last 500 years in China [J]. Acta Geographica Sinica (in Chinese), 34 (4): 329–341.
魏凤英. 2003. 现代气候统计诊断与预测技术 [M]. 北京: 气象出版社,105–113. Wei Fengying. 2003. Statistical Diagnosis and Prediction Techniques of Modern Climate (in Chinese) [M]. Beijing: China Meteorological Press, 105–113.
Wang B, Xiang B Q, Lee J Y. 2013. Subtropical High predictability establishes a promising way for monsoon and tropical storm predictions[J]. Proc. Natl. Acad. Sci. USA, 110: 2718–2722.
Wilby R L, Wigley T M L. 2000. Precipitation predictors for downscaling:Observed and general circulation model relationships [J]. International Journal of Climatology, 20: 641–661.
徐国昌. 1997. 中国干旱半干旱区气候变化 [M]. 北京: 气象出版社,101. Xu Guochang. 1997. Climate Change in China Arid and Semi-arid Areas (in Chinese) [M]. Beijing: China Meteorological Press, 101.
袁景凤, 吴晓曦. 2000. 一种新的多因子综合预报方法及其预测能力评估 [J]. 应用气象学报, 11 (S1): 98–102. Yuan Jingfeng, Wu Xiaoxi.2000. A new multifactor synthesize prediction method and its forecast performance assessment [J]. Journal of Applied Meteorological Science(in Chinese), 11(S1): 98–102.
章基嘉, 孙照渤, 陈松军. 1981. 对自然正交函数稳定性条件的讨论 [J].气象学报, 39 (1): 82–88. Zhang Jijia, Sun Zhaobo, Chen Songjun.1981. On the stability of empirical orthogonal function (EOF) [J]. Acta Meteorologica Sinica (in Chinese), 39 (1): 82–88.
章基嘉, 孙照渤, 兰国明. 1979. 亚洲500毫巴候平均环流的天气统计学分析 [J]. 南京气象学院院报, (1): 33–41. Zhang Jijia, Sun Zhaobo,Lan Guoming. 1979. Weather statistical analysis of Asian 500 mb mean circulations [J]. Journal of Nanjing Institute of Meteorology (in Chinese),(1): 33–41.
朱乾根, 林锦瑞, 寿绍文, 等. 2007. 天气学原理和方法 [M]. 北京: 气象出版社, 343. Zhu Qian’gen, Lin Jinrui, Shou Shaowen, et al. 2007.Principles and Methods of Meteorology (in Chinese) [M]. Beijing: China Meteorological Press, 343.
Zhang X S, Wu K J, Wang B, et al. 2013. The low-frequency variance of the ocean surface wave field in the area of the Antarctic Circumpolar Current [J]. Acta Oceanol. Sin., 32 (5): 15–21.

