Grbner-Shirshov Bases for Universal Algebras*
L A Bokut,Chen Yuqun(1.School of Mathematical Sciences,South China Normal University,Guangzhou 510631,China;2.Sobolev Institute of Mathematics,Novosibirsk State University,Novosibirsk 630090,Russia)
Gr bner bases and Gr bner-Shirshov bases were invented independently by A. I. Shirshov for ideals of free (commutative,anti-commutative)non-associative algebras[1-2],free Lie algebras[2-3]and implicitly free associative algebras[2-3](see also [4 -6]),by Hironaka[7]for ideals of the power series algebras (both formal and convergent),and by Buchberger[8]for ideals of the polynomial algebras.
As it is well known,Gr bner-Shirshov (GS for short)bases method for a class of algebras is based on a Composition-Diamond lemma (CD-lemma for short)for the class. A general form of a CD-lemma over a field k is as follows.
Composition-Diamond lemma Let M(X)be a free algebra generated by a set X of a category M of algebras over k,(N,≤)a linear basis (normal words)of M(X)with a monomial ordering ≤,S⊂M(X)andⅠd(S)the ideal of M(X)generated by S. Then the following statements are equivalent:
(a)S is a Gr bner-Shirshov basis in(X).
In some exceptional cases (dialgebras,conformal algebras)(a)⇒(b)⇔(c),but not (b)⇒(a).
How to establish a CD-lemma for the free algebra(X)?Following the idea of Shirshov,one needs
1)to define appropriate linear basis (normal words)N of(X);
2)to find a monomial ordering on N;
3)to find normal S-words;
4)to define compositions of elements in S (they may be compositions of intersection,inclusion and left(right)multiplication,or may be else);
5)to prove two key lemmas:
Lemma 1 Let S be a GS basis. Then any element of Ⅰd(S)is a linear combination of normal Swords.
Lemma 2 Let S be a GS basis,[a1s1b1]and[a2s2b2]normal S-words. If w =is trivial modulo(S,w).
Let the normal words N of the free algebra(X)be a well-ordered set and 0≠f(X). Denote bythe leading word of f. f is called monic if the coefficient ofis 1.
A well ordering on N is monomial if for any u,v,wwhere w|u=w|xuand w|v=w|xv.
For example,let X be a well-ordered set and X*the free monoid generated by X. We define the deg-lex ordering on X*:to compare two words first by length and then lexicographically. Then,such an ordering is monomial on X*.
An S-word u|sis normal if
There are two kinds of compositions,a (intersection (inclusion))composition (s1,s2)wof two polynomials relative to w =“lcm”()N(X)and a(left (right)multiplication)composition Comw(s)of one polynomial relative to w =N(X). Namely,for monic polynomial s1,s2,s,and Comw(s)=vs or sv correspondingly.
For example,let us start with the concepts of nonunique common multiple and least common multiple of two words u,vX*. A common multiple cm(u,v)means that cm(u,v)=a1ub1=a2vb2for some ai,biX*. Then lcm(u,v)means that some cm(u,v)contains some lcm(u,v)as a subword:cm(u,v)=c·lcm(u,v)·d with c,dX*,where u and v are the same subwords in both sides. To be precise,(a trivial lcm(u,v));

Main applications
· normal forms;
· word problems;conjugacy problem;
· rewriting system;
· automata theory;
· embedding of algebras into simple algebras and two-generated algebras;
· extensions of groups and algebras;
· PBW type theorems;
· homology;
· Dehn function;complexity;growth function;Hilbert series;etc.
Since 2006,there were some 30 master theses and 4 PhD theses,more then 30 published papers in JA,IJAC,Comm Algebra,Algebra Coll and other Journals and Proceedings. There were organized 2 International conferences (2007,2009)with E Zelmanov as chairman of the program committee and several workshops.We are going to review some of the papers and published three survey papers[9-11]. Our main topic is GS bases method for different varieties (categories)of linear (Ω-)algebras over a field k or a commutative algebra K over k:associative algebras (including group(semigroup)algebras),tensor product of free associative algebras,Lie algebras,dialgebras,conformal algebras,pre-Lie (Vinberg right (left)symmetric)algebras,Rota-Baxter algebras,metabelian Lie algebras,L-algebras,semiring algebras,category algebras,etc. There are some applications particularly to new proofs of some known theorems.
1 Gröbner-Shirshov bases theory for some new classes of (universal)algebras
In this section,we review some new CD-lemmas for tensor product of free associative algebras,Lie algebras over a commutative algebra,dialgebras,pre-Lie(Vinberg right (left)symmetric)algebras,Rota-Baxter algebras,metabelian Lie algebras,L-algebras,semiring algebras,associative algebras with multiple operations,differential algebras,category algebras,non-associative algebras over a commutative algebra,S-act algebras,etc. There are some applications for mentioned algebras.
In[12],GS bases method was initiated for a category of k-algebra with the free object k
In[13],GS bases method was found for Lie algebras over a commutative algebra K. For this category free objects are“double”free Lie algebras,i.e.,free Lie algebra Liek[Y](X)over free commutative algebra k[Y]. Then N(Y,X)=[Y]NLSW(X),where NLSW(X)is the set of non-associative (Lie)Lyndon-Shirshov(LS for short)words in X. There are both kinds of compositions mentioned above,(f,g)wand Comw(f).Actually this case is more difficult than the case of Lie algebras over a field. There are two proofs for the last case. In the original Shirshov's proof[3],it was used implicitly that one element set {s},sLiek(X)is a GS basis in the free associative algebra k
A key lemma in our proof is
Lemma 3 Let S be a Lie GS basis in Liek[Y](X)and (asb)a normal S-word. Then
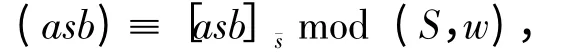
As an application,it was given another proofs that Shirshov's and Cartier's examples of Lie algebras over commutative algebras are not embeddable into associative algebras over the same commutative ones. Also it was proved that Cohn's examples[17]LieK(x1,x2,x3|y3x3=y1x1+y2x2)for K =k[y1,y2,y3|=0],chk=p=2,3,5,have the same property.
In[18],CD -lemma was established for metabelian Lie algebras.
A Lie algebra L is called a metabelian Lie algebra if (L2)2=0.
Let Lie(2,2)(X)be a free metabelian Lie algebra on X over k. A linear basis of any free polynilpotent Lie algebra L = Lie (n1,n2,…,nk)(X),(((Ln1)n2)…)nk= 0,was found in [19]using Shirshov's method[3]. For Lie(2,2)it is N(X)={xi,((xi1,xi2)…xim),i1>i2≤i3≤…≤im},where X={xi|iⅠ}is a linear ordered set. For u,vN(X)there are 5 types of lcm(u,v). Three of them was found by Talapov[20]and another 2 he missed. Actually from the CD-lemma for metabelian Lie algebras it does not follow Shirshov's result that the word problem is solvable for this class of algebras. Shirshov proved the residual finiteness of any finitely presented metabelian Lie algebra. Then the result follows.
Let (A,◦,·,θ,1)be a semiring,i.e.,(A,◦,θ)is a commutative monoid,(A,·,1)is a monoid,and θ·a=a·θ =θ,· is distributive relative to ◦from left and right:(a ◦b)c=ac ◦bc,c(a ◦b)=ca ◦cb. The semiring (A,◦,·,θ,1)is commutative if (A,·,1)is a commutative monoid.
The class of semirings is a variety. So a free semiring Rig
In[21],CD-lemma was proved for free semiring algebras kRig
An Ω-algebra A is a k-linear space with the linear operator set Ω on A.
In[24],we establish GS bases method for associative Ω-algebras,where Ω consists of n-ary operations,n≥1.
There are two kinds of compositions:intersection and inclusion.
As applications,we give linear bases for free Rota-Baxter k-algebra of weight λ and λ-differential algebra,where a Rota-Baxter k-algebra is an associative algebra R with a k-linear operation P:R →R satisfying the Rota-Baxter relation:

and a λ-differential algebra over k is an associative kalgebra R together with a k-linear operator D:R →R such that
D(xy)=D(x)y+xD(y)+λ D(x)D(y),∀x,yR.
In[25],GS bases method for Rota-Baxter algebras over a field of characteristic 0 is found.
There are four kinds of compositions:intersection,inclusion and left (right)multiplication.
As application,we prove that every countably generated Rota-Baxter algebra with weight 0 can be embedded into a two-generated Rota-Baxter algebra.
Another important application is PBW theorem for dendriform algebra which is a conjecture of L Guo.
A dendriform algebra is a k-linear space D with two binary operations ≺and ≻such that for any x,y,zD,
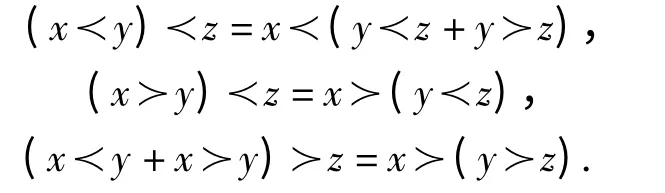
Suppose that (D,≺,≻)is a dendriform algebra over k with a linear basis X={xi|iⅠ}. Let xi≺xj={xi≺xj},xi≻xj={xi≻xj},where {xi≺xj}and {xi≻xj}are linear combinations of xX. Then D has an expression by generators and defining relations
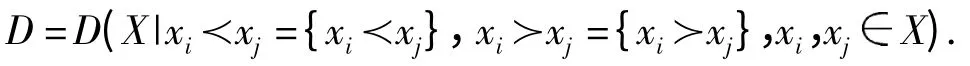
Denote by

where RB(X)is the free Rota-Baxter algebra generated by X. Then U(D)is the universal enveloping Rota-Baxter algebra of D.
The following result is obtained[26]:every dendriform algebra over a field of characteristic 0 can be embedded into its universal enveloping Rota-Baxter algebra.
A non-associative A is called a right-symmetric(or pre-Lie)algebra if A satisfies the following identity(x,y,z)=(x,z,y)for the associator (x,y,z)=(xy)zx(yz).
In[27],GS bases method is found for Pre-Lie algebras. As an application,we give a GS basis for the universal enveloping right-symmetric algebra of a Lie algebra. From this it follows PBW theorem for Lie algebra and right-symmetric algebra (Segal's theorem).
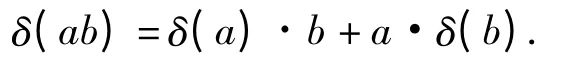
GS bases method for differential algebras is established[28].
As applications,there are given linear bases for free Lie-differential algebras and free commutative-differential algebras,respectively.
An L-algebra is a k-linear space L equipped with two binary k-linear operations ≺,≻:L⊗L→L verifying the so-called entanglement relation:

In [29],GS bases method for L-algebras is found.
There are two kinds of compositions:inclusion and right multiplication.
As applications,we give linear bases of a free dialgebra (Loday's theorem)and the free product of two L-algebras,and the following embedding theorems for L-algebras are obtained:1)Every countably generated L-algebra over a field k can be embedded into a twogenerated L-algebra. 2)Every L-algebra over a field k can be embedded into a simple L-algebra. 3)Every countably generated L-algebra over a countable field k can be embedded into a simple two-generated L-algebra. 4)Three arbitrary L-algebras A,B,C over a field k can be embedded into a simple L-algebra generated by B and C if |k|≤dim(B* C)and |A|≤|B* C|,where B* C is the free product of B and C.
A k-linear space D equipped with two bilinear multiplications ├and ┤is called a dialgebra,if both├and ┤are associative and
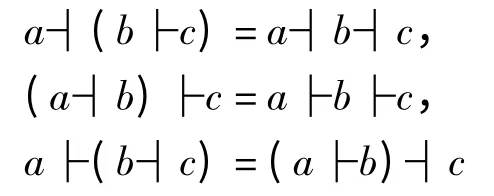
In[30],GS bases method for dialgebras is given. As results,we give linear bases for the universal enveloping algebra of a Leibniz algebra (Aymon-Grivel's theorem),the bar extension of a dialgebra,the free product of two dialgebras,and Clifford dialgebra. We obtain some normal forms for algebras mentioned the above.
GS bases method for small categories is established[31]. As applications,we give linear bases for the simplicial category (a classical result)and the cyclic category (A. Cohen's theorem)respectively.
GS bases method for non-associative algebras over commutative algebras is given[32]. As an application,it is shown that each countably generated non-associative algebra over an arbitrary commutative algebra K can be embedded into a two-generated non-associative algebra over K.
In [33],it is investigated the relationship between the GS bases in free associative algebras,free left modules and“double-free”left modules (that is,free modules over a free algebra). We first give the Chibrikov's CD-lemma for modules and then we show that the Kang-Lee's CD-lemma follows from this lemma. As applications,we give linear bases for the following modules:the highest weight module over a Lie algebra sl2,the Verma module over a Kac-Moody algebra,the Verma module over the Lie algebra of coefficients of a free conformal algebra,and a universal enveloping module for a Sabinin algebra.
A λ-differential associative algebra with multiple operators is a λ-differential algebra R with a set Ω of multi-linear operators.
GS bases method for λ-differential associative algebras with multiple operators is established[34]. As an application,a linear basis for the free λ-differential Rota-Baxter algebra is given and then normal forms is obtained for such an algebra which is the same as one in[24].
Let A be an associative algebra over a field k and S a monoid of linear operators on A. Then A is called an S-act algebra if A is an S-act with the action s(a)satisfying
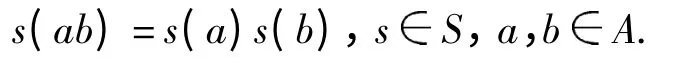
In[35],the“double free”S-act algebra (i.e.,a free S-act algebra,where S is a free semigroup)is constructed. Then GS bases theory for S-act algebras is established,where S is an arbitrary semigroup. As an application,a GS basis of free Chinese monoid-act algebra is given and hence a linear basis of free Chinese monoid-act algebra is obtained.
2 Applications
In this section,we review some applications of GS bases method (CD-lemmas)mentioned in the above section and CD-lemma for associative algebras.
In[36],it is generalized the Shirshov's composition lemma for associative algebras by replacing the monomial ordering for“S-partially monomial”ordering of words. As applications,we give a new proof of Britton lemma for HNN extensions of groups. Also a GS basis of the alternating group is obtained.
In[37],it is dealing with Schreier extensions of group

of A by B. If B is a cyclic or a free abelian group,there are classical necessary and sufficient conditions for C to be a Schreier extension of A by B in terms of the factor set of B. In[38],it is mentioned that for any B it is difficult to find an analogous conditions.Actually this problem was solved in[37]using the GS bases technique. As applications there were given new proofs of above conditions for cyclic and free abelian cases,as well as for the case of HNN-extensions.
The same kind of result was established for Schreier extensions of associative algebras[39]. An algebrais called a (singular)extension of the algebra M by B if M2=0,M is an ideal ofand/M≅B as algebras. In [39],singular extensions are studied from the GS bases viewpoint. Namely,even though extensions correspond to cocycles,the reconstruction of an extension from a cocycle can be applied to every 2-cochain of B with coefficients in M. This means that every 2-cochain φ gives rise to a certain associative algebra A(φ)presented by generators and relations. The main observation of the paper[39]is that the relations of A(φ)form a GS basis if and only if the cochain φ is a cocycle (so the algebra A(φ)is a singular extension of B by M). This implies the main result of this paper:an algorithmic procedure to check the extension condition.
Let Uq(AN)be the Drinfeld-Jimbo quantum group of type AN. In [40],by using GS bases,we give a simple (but not short)proof of the Rosso-Yamane theorem on PBW basis of Uq(AN)(see also[41]).
In[42],a simple analysis of the word problem for Novikov'sp1p2(P)and Boone's groups G(T,q)based on Gröbner-Shirshov bases technique is given(see also[43 -44]).
In[45],a GS basis for the Chinese monoid is obtained and an algorithm for normal form of the Chinese monoid is given. It gives new proof of some results in Cassaigne,etc[46].
In[47],an alternative approach to the definition of LS words (both associative and Lie)were found via free anti-commutative algebra AC(X)over a field.Namely for some ordering of non-associative words,we have Lie(X)=AC(X|S),where S is an anti-commutative GS basis and Ⅰrr(S)=NLSW(X). Moreover,a linear basis N(X)in this ordering of AC(X)consists of words[u]with the property u =(v)k,where vALSW(X),k≥1. The ordering is fulfilled the property[u]>[v]if u >v lexicographically (a prefix of an associative word is greater than the word).
The same kind of result was established in[48]for Hall basis of a free Lie algebra for an ordering with condition[u]>[v]if u >v in the deg-lex ordering.
In[49],a free inverse semigroup
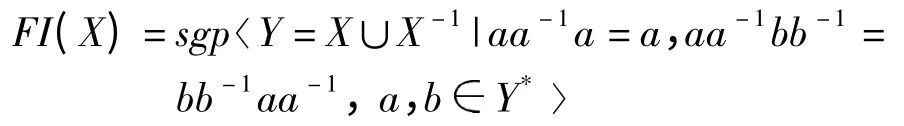
was studied. A GS basis and normal forms were found for the semigroup. This gives simple proofs of substantial refinements of results in Polyakova-Schain[50].
In [51],by using GS bases,a straightforward proof for Artin-Markov normal form theorem for braid groups is given (see also[52]).
In[53],by using CD-lemma for L-algebras[29],we give a GS basis of the free dendriform diaglebra as a quotient algebra of an L-algebras. Then we obtain the Hilbert series and Gelfand-Kirillov dimension of the free dendriform dialgebra generated by a finite set.
In[54],by using GS bases,we show that in the following classes,each (resp. countably generated)algebra can be embedded into a simple (resp. twogenerated)algebra:associative differential algebras,associative Ω-algebras,associative λ-differential algebras. We show that in the following classes,each countably generated algebra over a countable field k can be embedded into a simple two-generated algebra:associative algebras,semigroups,Lie algebras,associative differential algebras,associative Ω-algebras,associative λ-differential algebras. Also we prove that any countably generated module over a free associative algebra k
In[55],we prove that two-generator one-relator groups with depth less than or equal to 3 can be effectively embedded into a tower of HNN-extensions in which each group has the effective standard normal form in the sense of Bokut-Kukin[56]. We give an example to show how to deal with some general cases for one-relator groups.
In[57],we give a GS basis of the braid group Bn+1in Adyan-Thurston generators. As results,a new algorithm for getting the Adyan-Thurston normal form is obtained,and a new proof that the braid semigroupis the subsemigroup in Bn+1is given.
In[58],by using the CD-lemma for non-associative algebras invented by A. I. Shirshov in 1962,we give GS bases for free Pre-Lie algebras and the universal enveloping non-associative algebra of an Akivis algebra,respectively. As applications,we show I. P.Shestakov's result that any Akivis algebra is linear and D. Segal's result that the set of all good words in X**forms a linear basis of the free Pre-Lie algebra PLie(X)generated by the set X.
In[59],a Lie GS basis is found for any free partially commutative Lie algebra.
In[60],we give two explicit (quadratic)presentations of the plactic monoid in row and column generators correspondingly. Then we give direct independent proofs that these presentations are GS bases of the plactic algebra in deg-lex orderings of generators. From CD-lemma for associative algebras it follows that the set of Young tableaux is the Knuth normal form for plactic monoid.
Kukin construction. Let P=sgp
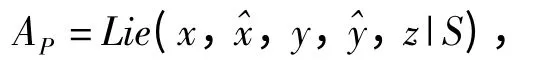
where S consists of the following relations:
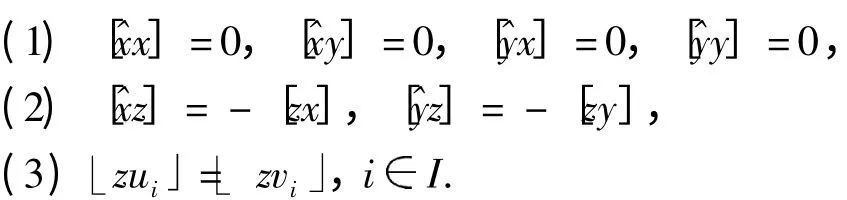
Here,⎿zu」means the left normed bracketing.
Drinfeld-Kohno construction. Let n >2 be an integer. The Drinfeld-Kohno Lie algebra Lnover Z is defined by generators tij=tjifor distinct indices 1≤i,j≤n-1,and relations
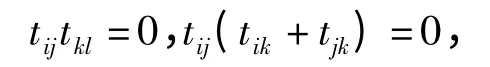
where i,j,k,l are distinct.
In[61],GS bases for Drinfeld-Kohno Lie algebra Lnand Kukin Lie algebra APare obtained. As an application,we show that Lnis an iterated semidirect product of free Lie algebras. Another application is Kukin's result:if semigroup P has the undecidable word problem then the Lie algebra APhas the same property. It gives another proof of the theorem of the first author that the word problem for Lie algebras is algorithmically undecidable (1972). For semigroups and groups there are famous results by Markov-Post (1947)and Novikov (1955)respectively.
3 Some prospects
We are trying to establish Gröbner-Shirshov bases theory for Novikov algebras,strict monoidal categories,modules over an associative conformal algebra,associative n-conformal algebras,Nijenhuis algebras,etc. We will give some new applications of the mentioned Composition-Diamond lemmas,for example, automatic structures for some semigroups,PBW theorems,homology for some semigroup algebras,Dehn functions for some groups,embedding algebras into two generated simple algebras,word problems for some algebras,and so on.
[1]Shirshov A I. Some algorithmic problem for ε-algebras[J]. Sibirskii Matematichskii Zhurnal,1962,3:132 -137.
[2]Bokut L A,Latyshev V,Shestakov I,et al.Selected works of A.I. Shirshov[M].Trs:Bremner M,Kotchetov M V.Basel,Boston,Berlin:Birkhäuser,2009.
[3]Shirshov A I. Some algorithmic problem for Lie algebras[J]. Sibirskii Matematichskii Zhurnal,1962,3(2):292-296.
[4]Bergman G M. The diamond lemma for ring theory[J].Advances in Mathematics,1978,29:178 -218.
[5]Bokut L A. Imbeddings into simple associative algebras[J]. Algebra Logika,1976,15:117 -142.
[6]Bokut L A,Chen Y Q. Gröbner-Shirshov bases for Lie algebras:After A.I. Shirshov[J]. Southeast Asian Bulletin of Mathematics,2007,31:1057 -1076.
[7]Hironaka H.Resolution of singularities of an algebraic variety over a field if characteristic zero:Ⅰ,Ⅱ[J]. Mathematische Annalen,1964,79:109 -203;205 -326.
[8]Buchberger B.An algorithmical criteria for the solvability of algebraic systems of equations[J]. Aequationes Mathematicae,1970,4:374 -383.
[9]Bokut L A,Chen Y Q. Gröbner-Shirshov bases:Some new results[C]∥Shum K P,Zelmanov E,Zhang J P,et al. Advance in Algebra and Combinatorics. Singapore:World Scientific,2008:35 -56.
[10]Bokut L A,Chen Y Q. Gröbner-Shirshov bases and their calculation[J]. Bulletin of Mathematical Sciences,doi:10.1007/s13373 -014 -0054 -6.
[11]Bokut L A,Chen Y Q,Shum K P. Some new results on Gröbner-Shirshov bases[C]∥Hemakul W,Wahyuni S,Sy P W. Advances in Algebraic Structures. Singapore:World Scientific,2012:53 -102.
[12]Bokut L A,Chen Y Q,Chen Y S. Composition-Diamond lemma for tensor product of free algebras[J]. Journal of Algebra,2010,323:2520 -2537.
[13]Bokut L A,Chen Y Q,Chen Y S. Gröbner-Shirshov bases for Lie algebras over a commutative algebra[J]. Journal of Algebra,2011,337:82 -102.
[14]Cartier P. Remarques sur le théorème de Birkhoff-Witt[J]. Annali della Scuola Norm Sup di Pisa série Ⅲ,1958,Ⅻ:1 -4.
[15]Shirshov A I. On the representation of Lie rings in associative rings[J]. Uspekhi Matematicheskikh Nauk,1953,8(5):173 -175.
[16]Shirshov A I. On free Lie rings[J]. Mathematical Sbornik,1958,45(2):113 -122.
[17]Cohn P M. A remark on the Birkhoff-Witt theorem[J].Journal of the London Mathematical Society,1963,38:197-203.
[18]Chen Y S,Chen Y Q. Gröbner-Shirshov bases for metabelian Lie algebras[J]. Journal of Algebra,2012,358:143 -161.
[19]Bokut L A. A basis of free polynilpotent Lie algebras[J].Algebra Logika,1963,2(4):13 -19.
[20]Talapov V V. Algebraically closed metabelian Lie algebras[J]. Algebra Logika,1982,21(3):357 -367.
[21]Bokut L A,Chen Y Q,Mo Q H. Gröbner-Shirshov bases for semirings[J]. Journal of Algebra,2013,378:47 -63.
[22]Blass A. Seven trees in one[J]. Journal of Pure and Applied Algebra,1995,103:1 -21.
[23]Fiore M,Leinster T. An objective representation of the Gaussian integers[J]. Journal of Symbolic Computation,2004,37:707 -716.
[24]Bokut L A,Chen Y Q,Qiu J J. Gröbner-Shirshov bases for associative algebras with multiple operations and free Rota-Baxter algebras[J]. Journal of Pure and Applied Algebra,2010,214:89 -100.
[25]Bokut L A,Chen Y Q,Deng X M. Gröbner-Shirshov bases for Rota-Baxter algebras[J]. Siberian Mathematical Journal,2010,51:978 -988.
[26]Chen Y Q,Mo Q H. Embedding dendriform algebra into its universal enveloping Rota-Baxter algebra[J]. Proceedings of the American Mathematical Society,2011,139:4207 -4216.
[27]Bokut L A,Chen Y Q,Li Y. Gröbner-Shirshov bases for Vinberg-Koszul-Gerstenhaber right-symmetric algebras[J]. Journal of Mathematical Sciences,2010,166:603 -612.
[28]Chen Y Q,Chen Y S,Li Y. Composition-Diamond lemma for differential algebras[J]. The Arabian Journal for Science and Engineering,2009,34:135 -145.
[29]Bokut L A,Chen Y Q,Huang J P. Gröbner-Shirshov bases for L-algebras[J]. International Journal of Algebra and Computation,2013,23:547 -571.
[30]Bokut L A,Chen Y Q,Liu C H.Gröbner-Shirshov bases for dialgebras[J]. International Journal of Algebra and Computation,2010,20:391 -415.
[31]Bokut L A,Chen Y Q,Li Y. Gröbner-Shirshov bases for categories[C]∥Bai C M,Loday J L. Operads and Universal Algebra. Singapore:World Scientific,2012,9:1 -23.
[32]Chen Y Q,Li J,Zeng M J. Composition-Diamond lemma for non-associative algebras over a polynomial algebra[J]. Southeast Asian Bulletin of Mathematics,2010,34:629 -638.
[33]Chen Y Q,Chen Y S,Zhong C Y. Composition-Diamond lemma for modules[J]. Czechoslovak Mathematical Journal,2010,60:59 -76.
[34]Qiu J J,Chen Y Q. Composition-Diamond lemma for λdifferential associative algebras with multiple operators[J]. Journal of Algebra and its Applications,2010,9:223 -239.
[35]Zhang X. Gröbner-Shirshov bases for S-act algebras[J].Southeast Asian Bulletin of Mathematics,2010,34:791 -800.
[36]Chen Y Q,Zhong C Y. Gröbner-Shirshov basis for HNN extensions of groups and for the alternative group[J].Communications in Algebra,2008,36:94 -103.
[37]Chen Y Q. Gröbner-Shirshov basis for Schreier extensions of groups[J]. Communications in Algebra,2008,36:1609 -1625.
[38]Hall M Jr. The theory of groups[M]. New York:The Macmillan Company,1959.
[39]Chen Y Q. Gröbner-Shirshov basis for extensions of algebras[J]. Algebra Colloquium,2009,16:283 -292.
[40]Chen Y Q,Shao H S,Shum K P. On Rosso-Yamane theorem on PBW basis of Uq(AN)[J]. CUBO A Mathematical Journal,2008,10:171 -194.
[41]Bokut L A,Malcolmson P. Gröbner-Shirshov basis for quantum enveloping algebras[J]. Israel Journal of Mathematics,1996,96:97 -113.
[42]Chen Y Q,Chen W S,Luo R I. Word problem for Novikov's and Boone's group via Gröbner-Shirshov bases[J]. Southeast Asian Bulletin of Mathematics,2008,32:863 -877.
[43]Bokut L A. On a certain property of the Boone group:Ⅱ[J]. Algebra Logika,1967,6(1):1 -24.
[44]Bokut L A. On the Novikov groups[J]. Algebra Logika,1967,6(1):25 -38.
[45]Chen Y Q,Qiu J J. Gröbner-Shirshov basis for the Chinese monoid[J]. Journal of Algebra and its Applications,2008,7:623 -628.
[46]Cassaigne J,Espie M,Krob D,et al. The Chinese monoid[J]. International Journal of Algebra and Computation,2001,11:301 -334.
[47]Bokut L A,Chen Y Q,Li Y. Lyndon-Shirshov words and anti-commutative algebras[J]. Journal of Algebra,2013,378:173 -183.
[48]Bokut L A,Chen Y Q,Li Y. Anti-commutative Gröbner-Shirshov basis of a free Lie algebra[J]. Science in China:Series A,2009,52:244 -253.
[49]Bokut L A,Chen Y Q,Zhao X G. Gröbner-Shirshov beses for free inverse semigroups[J]. International Journal of Algebra and Computation,2009,19:129 -143.
[50]Poliakova O,Schein B M. A new construction for free inverse semigroups[J]. Journal of Algebra,2005,288:20-58.
[51]Chen Y Q,Mo Q H. Artin-Markov normal form for braid group[J]. Southeast Asian Bulletin of Mathematics,2009,33:403 -419.
[52]Bokut L A,Chaynikov V V,Shum K P. Markov and Artin normal form theorem for braid groups[J]. Communications in Algebra,2007,35:1 -11.
[53]Chen Y Q,Wang B. Gröbner-Shirshov bases and Hilbert series of free dendriform algebras[J]. Southeast Asian Bulletin of Mathematics,2010,34:639 -650.
[54]Bokut L A,Chen Y Q,Mo Q H. Gröbner-Shirshov bases and embeddings of algebras[J]. International Journal of Algebra and Computation,2010,20:875 -900.
[55]Chen Y Q,Zhong C Y. Gröbner-Shirshov basis for some one-relator groups[J]. Algebra Colloquium,2011,19:99-116.
[56]Bokut L A,Kukin G P. Algorithmic and combinatorial algebra[M]. Dordrecht:Kluwer Academic Publishers,1994.
[57]Chen Y Q,Zhong C Y. Gröbner-Shirshov bases for braid groups in Adyan-Thurston generators[J]. Algebra Colloquium,2013,20:309 -318.
[58]Chen Y Q,Li Y. Some remarks on the Akivis algebras and the Pre-Lie algebras[J]. Czechoslovak Mathematical Journal,2011,61:707 -720.
[59]Chen Y Q,Mo Q H. Gröbner-Shirshov bases for free partially commutative Lie algebras[J]. Communications in Algebra,2013,41:3753 -3761.
[60]Bokut L A,Chen Y Q,Chen W P,et al. New approaches to plactic monoid via Gröbner-Shirshov bases[J]. Journal of Algebra,arXiv:1106.4753.
[61]Chen Y Q,Li Y,Tang Q Y. Gröbner-Shirshov bases for some Lie algebras[J]. Siberian Mathematical Journal,arXiv:1305.4546.

