一种伽马传感器全温度范围补偿方法
马海,肖红兵,杨锦舟,唐海全
(中石化胜利石油工程有限公司钻井工艺研究院,山东 东营257017)
0 引 言
自然伽马测井不同温度段对应的伽马传感器的测量值不同,伽马传感器的计数涨落起伏随温度升高变化较大,从而导致测量不准确不稳定[1-2]。如果不考虑温度对伽马传感器的影响,在刻度过程中选取同样的系数,则测量值必定存在着一定的误差,因此有必要对伽马传感器进行全温度范围的补偿修正。
为消除温度对伽马传感器产生的非线性影响,目前国内外研究方法包括硬件补偿和软件补偿2种方法。硬件补偿方法由于受到电路中电子元器件漂移等因素的影响,导致整个测量系统可靠性差且精度低,无法做到全程补偿,实际使用过程中其应用受到限制[3-5]。软件补偿方法主要包括2类,一类是预先依靠经验假设出补偿方程,再通过多项式拟合或插值的方法进行计算,如曲线拟合法、分段线性插值法等[6],这类方法很容易导致“欠拟合”和“过拟合”现象的发生,以及病态方程的出现,从而使得适应性较低,精度低;而另一类方法采用人工智能方法,如神经网络算法、支持向量机等[7-10],先进行训练学习,获得大量的数据,然后再进行加权计算得出结果,这种方法计算量很大,容易陷入局部极值。
本文提出一种伽马传感器全温度范围补偿方法,通过选取合适的基函数建立伽马传感器测量值全温度补偿模型,并提出一种模型评价函数对模型参数进行优化,实现全温度范围内补偿,从而提高了仪器的测量精度。
1 温度点及样本数据段选取
1.1 温度点选取
将伽马传感器放入温度试验箱内,按照图1的仪器温度试验曲线调节试验箱的温度到试验要求的温度,箱内温度应均匀升高,选定一个初始温度T0,向上每间隔ΔT恒温保持Δh时间后,记录伽马传感器测量值,升至仪器的最高工作温度Tmax,恒温保持后记录伽马传感器测量值。
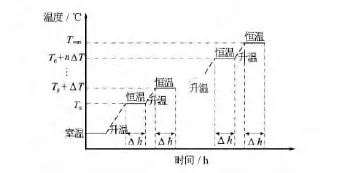
图1 仪器温度试验曲线
1.2 样本数据段选取
根据数据分析需要选取数据窗口(每次选定的数据量)大小,选取一定的步长(每次移动的数据个数),按步长逐次移动数据窗口(见图2),计算每次移动后数据窗口内数据的误差值,选取其中最小的误差值对应的数据窗口作为最终选取的样本数据段。误差eRMS为
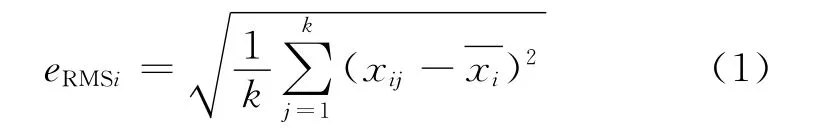
式中,k为数据窗口大小;i为数据窗口移动次数;xij为数据窗口第i次移动后的窗口内的第j个数据;为数据窗口第i次移动后的窗口内数据的平均值。
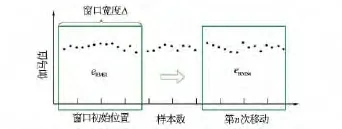
图2 利用数据窗口进行样本数据段选取
对数据窗口内的异常值(测量结果大大偏离正常范围的数值),在实际数据处理之前,应首先剔除。采用统计学中的3σ准则进行异常值检测与剔除。依据3σ准则,若采样数据的值处于平均值的3倍标准差之外,则被称为异常值。其标准差公式为

采样值中正常值为±3σ内的数值,超过则判定为异常值,进行剔除。
2 伽马传感器全温度补偿模型建立
2.1 模型建立
设伽马传感器的特性函数为y=f(x),其中y是传感器的输出,x是传感器的输入,增设温度参量,则特性函数变为y=f(x,T)。首先根据伽马传感器在温度影响下的特性曲线呈现非线性的特点,选取合适的基函数

然后建立伽马传感器测量值温度补偿模型
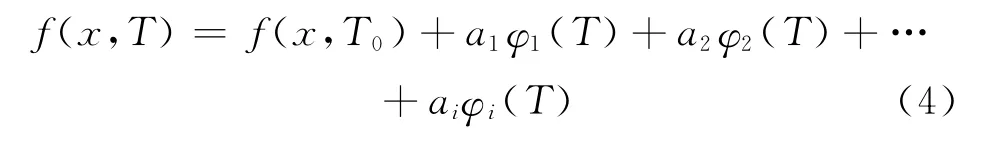
式中,{φi(T)},(i=1,2,…,k)为模型基函数;k为基函数个数;ai(i=1,2,…,k)为基函数加权系数。
该模型中基函数个数k的选取对于伽马传感器温度补偿效果尤为重要,k选择的小会导致误差较大,相关系数较小;而k选择的大,虽然对于给定温度点的拟合误差会很小,相关系数会较大,但会导致过拟合现象,使模型的泛化能力下降。为解决这个问题,提出一种评价函数
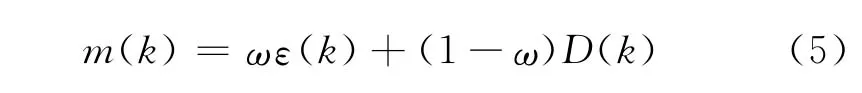
式中,ω为精确度和泛化度的折中系数;ε(k)为模型基函数个数为k时的精确度;D(k)为模型基函数个数为k时的泛化度;n1为样本点数目;n2为数据验证点数目。
为充分利用土地和大棚资源,提高单位面积土地产出率,增加农户经济效益,我们经过多年生产实践,总结出了草莓—甜瓜高产高效栽培模式,其主要栽培技术如下。
评价函数中折中系数ω的选取与模型样本数据点数目有着密切的关系,当数据点个数较多时,评价模型时更关注于精确度函数ε(k);当数据点个数较少时,泛化度函数D(k)对评价模型起到更大的作用。在计算模型泛化度时,数据验证点一般选取异于模型建立时的数据样本点。
2.2 模型参数求取
伽马传感器测量值全温度补偿模型参数包括基函数加权系数a1,a2,…,ai及基函数个数k,采用如下步骤进行求取。
(1)当k=1时,伽马传感器测量值温度补偿模型为f(x,T)=f(x,T0)+a1φ1(T),利用最小二乘方法求取加权系数a1,计算评价函数值m(1)。
(2)当k=i(i>1)时,伽马传感器测量值温度补偿模型为f(x,T)=f(x,T0)+a1φ1(T)+a2φ2(T)+…+aiφi(T),利用最小二乘方法求取加权系数a1,a2,…,ai,计算评价函数值m(i),比较m(i)和m(i-1)大小,如果m(i)<m(i-1),则令i=i+1,转到步骤(3),否则运算停止。
(3)重复步骤(2),直到找到最小评价函数值m(i),此时对应的基函数加权系数及基函数个数i即为最优伽马传感器测量值全温度补偿模型参数。
在上述步骤中利用最小二乘方法求取模型加权系数a1,a2,…,ai,具体运算过程如下。
令y=f(x,T)-f(x,T0),则伽马传感器测量值温度补偿模型可以转换为yi=a1φ1(Tj)+a2φ2(Tj)+…+aiφi(Tj),j=1,2,…,m。其中,m为拟合样本数目,待定系数al(l=1,2,…,i)的选择必须满足残差式(6),取极小值。

根据多元函数极值问题,E取极值的必要条件是

令
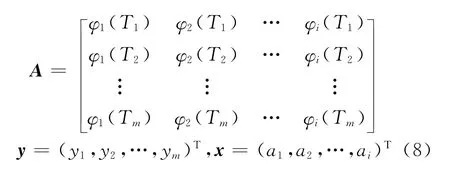
则
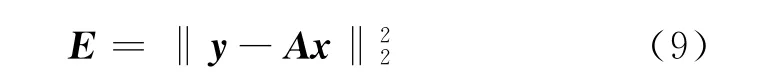
由此最小二乘拟合问题就转化为超定线性方程组的最小二乘解问题,即

通过最小二乘方法即可以得到待定系数a1,a2,…,ai。
利用上述方法可以实现伽马传感器全温度范围补偿。
3 应用实例
利用本文提出的方法对实际伽马传感器温度测试数据建立了全温度范围补偿模型。
样本数据段的异常值检测与剔除以151.8℃时的伽马传感器测试数据为例,该温度下共有192个样本数据,通过计算样本均值为250.86API,标准差σ为5.29API。图3给出了151.8℃时样本数据段的异常值检测与剔除结果。
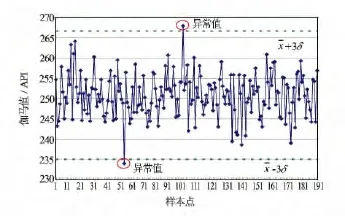
图3 样本数据段异常值检测与剔除
通过对所建立模型参数的求取,最终确定基函数个数k为4,基函数加权系数{ai}(i=1,2,…,k)为 {0.21746,-0.0055846,4.4636e-005,-1.1986e-007}。
表1给出了伽马传感器测量值及模型补偿值的具体数据比较。通过分析表1可以发现,该方法最大误差在误差允许范围之内,相关系数为0.9884,因此该方法是有效的,利用它可以提高仪器的测量精度。
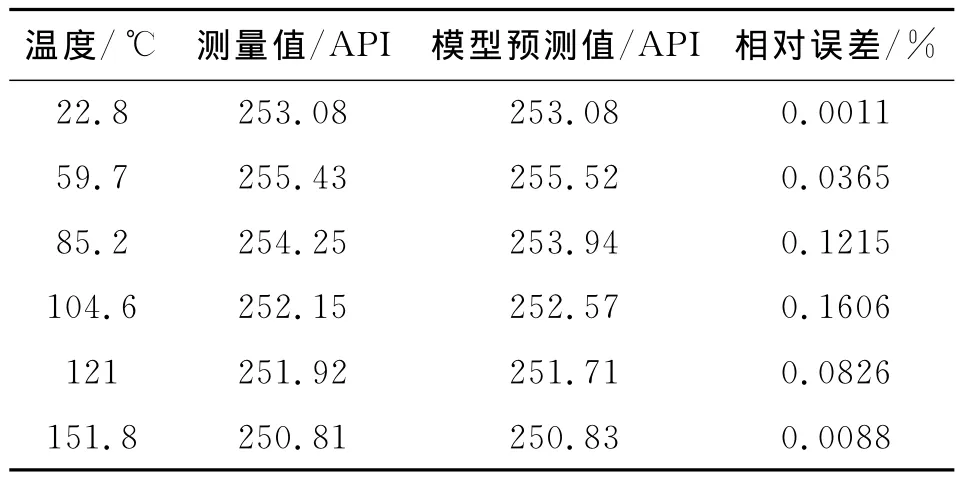
表1 伽马传感器温度补偿结果
4 结束语
针对伽马传感器的温度漂移造成测量误差的问题,提出了一种伽马传感器全温度范围补偿模型方法。通过全温度补偿温度点的确定以及样本数据的选取,可以有效筛选出伽马传感器随温度变化的数据样本,构建伽马传感器测量值全温度补偿模型可以消除测量过程中温度对伽马传感器测量值的影响,提高仪器测量精度。
[1]王金辉.温度补偿在自然伽马仪中的应用[J].江汉石油科技,2003,13(4):62-64.
[2]龙洋,王连科.石油生产测井多参数测量及温度线性化补偿[J].机械与电子,1997,15(1):27-28.
[3]王金辉.温度补偿技术在测井仪器中的应用[J].石油仪器,2006,20(5):86-89.
[4]Elton D Winemiller.Method and Apparatus for Temperature Compensation of Gamma Tools in MWD Enviroments[P].USA,5461230.1995.10.24.
[5]Raja J Paul Perinbam,Srinivasan S.A Continuously Variable Temperature Compensated Gamma Correction Circuit[J].IEEE Transactions on Consumer Electronics,1982,28(2):129-134.
[6]毋伟,李道明,毋涛.随钻测斜仪温度补偿方法的研究[J].电子测量与仪器学报,2000,14(3):64-66.
[7]王秀芳,句莉莉,魏春明,等.基于Elman神经网络的传感器补偿算法研究[J].科学技术与工程,2009,9(20):5987-5990.
[8]张妤,谢永华,穆丽新,等.基于支持向量机的电容式传感器温度补偿研究[J].传感器与微系统,2009,28(6):40-42.
[9]唐炜,徐晓苏.改进遗传神经网络在传感器温度补偿中的应用[J].电子测量与仪器学报,2008,22(1):62-67.
[10]于湘涛,张兰,郭琳瑞,等.基于小波最小二乘支持向量机的加速度计温度建模和补偿[J].中国惯性技术学报,2011,19(1):95-98.

