基于等效岩石组分理论的渗透率解释模型

张冲，张占松，张超谟

（1．长江大学油气资源与勘探技术教育部重点实验室，湖北 荆州434023；2．长江大学地球物理与石油资源学院，湖北 荆州434023）

0 引 言

不同途径获取的渗透率可归为有效渗透率和绝对渗透率［1］。通常获取绝对渗透率（简称渗透率）的方法有岩心分析法和测井计算法［2］，其中，岩心分析渗透率最为准确，是一种较直接的渗透率测量方法，常用来刻度测井计算的渗透率，但是受到采样点的限制，获得的渗透率值不够全面而且也不连续，因此，利用常规测井资料，研究渗透率与常规测井响应参数间的测井解释模型就显得尤为必要。

利用常规测井资料获取渗透率的思路有2种，一种是建立渗透率与各种储层参数、测井响应参数之间的统计模型，例如渗透率与孔隙度、自然伽马相对值的统计模型［3］、分流动单元建立的渗透率模型［4－7］、神经网络计算的渗透率模型［8－10］等；另 一 种方法是尝试通过岩石物理模型建立渗透率与储层特征参数之间的关系，例如 Wyllie－Rose渗透率测井解释模型［11］、Timur渗透率测井解释模型［12］等。2种方法互为补充，但 Wyllie－Rose方程、Timur方程在低渗透储层渗透率测井评价中，计算的渗透率与岩心分析的渗透率比较，误差较大。为此，以等效岩石组分理论为基础，依据电荷迁移与流体分子迁移相似性原理，在有效导电孔隙度基础上，提出有效流动孔隙度的概念，建立有效流动孔隙度与渗透率之间新的渗透率测井解释模型，并与Wyllie－Rose方程、Timur方程进行对比分析，验证模型的准确性。

1 Wyllie－Rose方程和Timur方程

Kozeny和Carman等研究认为渗透率与孔隙度成正比，与岩石单位体积比表面积成反比，基于此，建立了渗透率与孔隙度、岩石颗粒比表面积的简单关系，即Carman－Kozeny方程

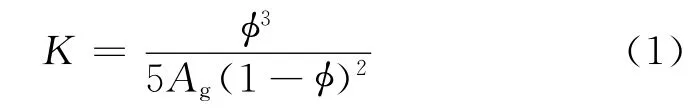
式中，K为渗透率，mD＊非法定计量单位，1mD＝0．987×10－3μm2，下同；φ为孔隙度，小数；Ag为岩石单位体积比表面积。

由于岩石颗粒比表面积很难用测井资料进行表征，因此 Wyllie和Rose对Carman－Kozeny方程进行了修改，方程中用束缚水饱和度替代了颗粒比表面积，Wyllie－Rose方程的一般形式表示为

式中，Swi为束缚水饱和度，小数；P、Q、R分别为可变系数，可通过岩心分析资料获取。

Timur等依据 Wyllie－Rose方程，以来自不同油田的156块砂岩岩心分析资料，建立了渗透率与孔隙度、束缚水饱和度的相关关系，简称Timur方程

2 基于等效岩石组分理论的渗透率测井解释模型（EREM）

2．1 等效岩石组分理论

在等效岩石组分理论中，将整个岩石等效为多个网格单元，对于每个网格单元，孔隙空间被划分成2个正交的组分（见图1）。分Pf平行于电势梯度，而组分Pp垂直于电势梯度。对于每个组分体积，组分Pf的离子迁移效率远比组分Pp高，Pf与Pp的体积比定义为孔隙结构效率c。依据孔隙结构效率的定义，结合串并联原理，Shang等［13］推导出了基于等效岩石组分的导电方程

图1 等效岩石组分模型

2．2 有效导电孔隙度

对于1块岩样（孔隙度φ和地层因素F），可以等效为具有相同岩石体积和相同地层因素，但是由固体骨架和平行于电势梯度的直毛细管组成。定义毛细管体积与岩石总体积的百分比为有效导电孔隙度。对于经典的毛细管模型，唯一的毛细管代表岩石的孔隙，这种情况下，阿尔奇公式中的a＝m＝1。

联合式（4）和式（5），

可以得到有效导电孔隙度的表达式

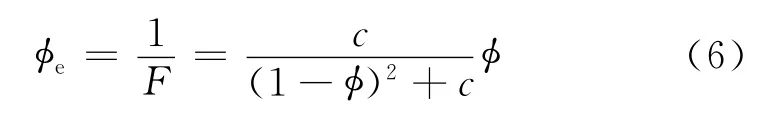
这里的有效导电孔隙度和后面提到的有效流动孔隙度与常见的有效孔隙度并不是一个概念，有效孔隙度指具有储集性质的有效孔隙体积占岩石体积的百分数，但并不是所有的有效孔隙贡献给离子的迁移或者流体的流动，有些孔隙非常有效，有些反导电孔隙度是对于具有相同离子迁移能力的岩石来说最小且最有效的孔隙，总孔隙度是一个标量，而有效导电或者有效流动孔隙度是一个向量，需要定义其方向，因为离子迁移效率或者流体流动的效率会随着其方向的变化而变化。

2．3 有效流动孔隙度

电荷的迁移与流体分子的迁移相似，电荷和流体的流量都受控于孔隙的几何形状和孔隙相互间的连通性。岩石等效元素模型可以用来研究岩石孔隙流体的流动。由于流体流动也受控于岩石的比表面积、单位孔隙体积的颗粒表面积的影响，且束缚水饱和度可以用来估算岩石的比表面积。又由于不被束缚水占据的孔隙空间控制着流体的流动，因此，支持流体迁移的孔隙空间一般比支持电荷迁移的孔隙空间小，因此有效流动孔隙度模型需要在有效导电孔隙度的基础上进行修改。

假如束缚水规则地分布在2种元素中，那么Pkp和Pkf的体积将成比例的减小。然而，由于受孔隙大小、连通性、流体性质及润湿性等因素影响，束缚水并不是规则分布。为了获取有效流动孔隙度，假设Vf＝c，则Vp＝1；假设束缚水饱和度为Swi，则赋存在元素Pf的束缚水饱和度为rSwi，r为比例因子。依据上述假设，元素Pkf的体积Vkf可以表示为

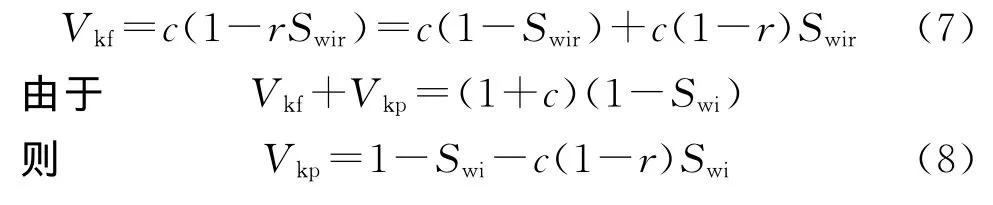
依据式（4），则修正后的孔隙结构效率ck为

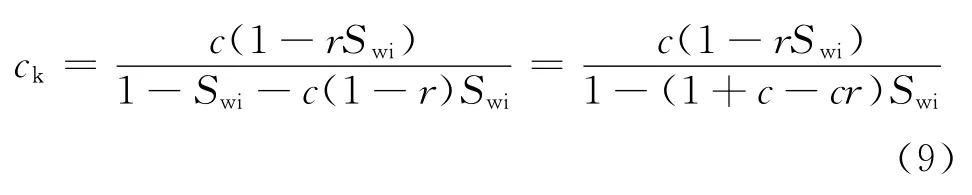
比例因子r表示束缚水在2种元素的分布状态，一般与束缚水饱和度存在一定的关系，已发表的文献资料表明［14］，r＝bSvwi，则ck可以更改为

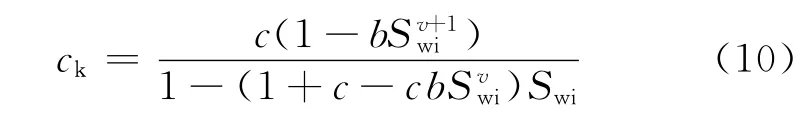
允许流体流动的孔隙度为φ（1－Swi），对照有效导电孔隙度表达式，有效流动的孔隙度可以修正为

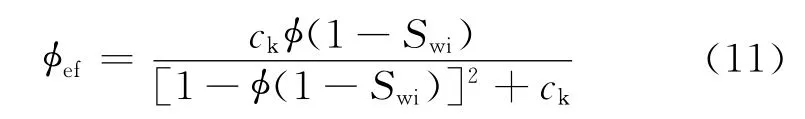
2．4 渗透率模型

由于有效流动孔隙度等效于岩样直毛细管孔隙，则与储层渗透率（取对数）应是一线性关系，关系如下

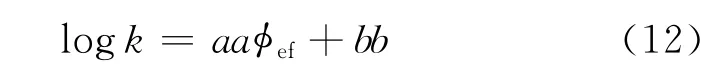
选取一定数量的代表性岩样，进行岩石物理实验测量，获取渗透率、孔隙度、地层因素及束缚水饱和度后，用式（4）、式（10）、式（11）和式（12）通过遗传算法［15］，不断调整参数b和v，建立渗透率与有效流动孔隙度之间的最优关系式。一旦该关系被建立，即可利用孔隙度、地层因素及束缚水饱和度计算储层的渗透率。

3 渗透率模型的对比分析

选取四川盆地须家河组29块具有代表性的岩样，孔隙度值介于5%～20%，渗透率值介于0．05～100mD，属典型的低－特低渗透率储层岩样。对这29块岩样进行了物性分析、岩石电阻率及核磁共振实验测量，分别获取了这29块岩样的孔隙度、渗透率、地层因素及核磁束缚水饱和度。图2至图4分别为29块岩样的渗透率与孔隙度、渗透率与束缚水饱和度、地层因素与孔隙度的相关关系图，可以看出，渗透率与孔隙度、束缚水饱和度的单相关关系较差。

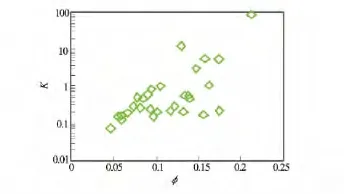
图2 渗透率与孔隙度的相关关系

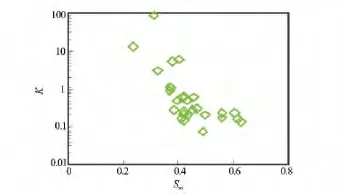
图3 渗透率与束缚水饱和度的相关关系

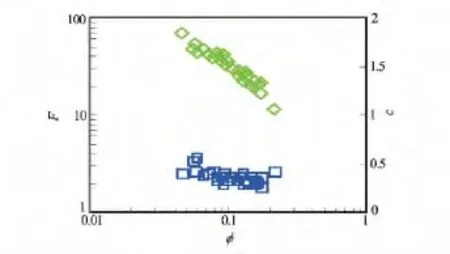
图4 地层因素、孔隙结构效率c与孔隙度的相关关系

图5 渗透率与有效流动孔隙度优化模型

依据这29块岩样的实验数据，获取了Wyllie－Rose方程中的系数P、Q、R值，分别为0．628、1．65、4．28。依据相同的实验数据，首先通过式（4）求取了每块岩样的孔隙结构效率c，绘制孔隙结构效率c与孔隙度的交会图（见图4），发现所选岩样的孔隙结构效率c值基本为一常数，取其平均值为0．346；然后建立拟合函数，如式（13），采用遗传算法编程获取了渗透率与有效流动孔隙度的最优解，获取了优化参数aa＝50．992，bb＝－1．3351，b＝1．96，v＝1．01，其中渗透率与有效流动孔隙度的关系见图5，其相关系数达到0．9073。

分别用 Wyllie－Rose模型、Timur模型和EREM模型计算这29块岩样的渗透率，把计算的结果与岩心分析的渗透率进行对比（见图6）。分析认为3种模型中，Timur模型计算的效果最差，EREM模型优于Wyllie－Rose模型，特别在渗透率低于0．2mD和高于3mD这个区间效果更明显。

图6 3种模型计算的渗透率与岩心分析渗透率的对比

图7 3种渗透率模型的应用效果图（××1井）

4 应用实例

渗透率测井解释模型计算的渗透率相对于岩心分析渗透率的优势在于全井段连续处理，为了将EREM渗透率模型应用于实际资料的处理，首先需要确定储层的束缚水饱和度，本文采用如下经验公式［3］进行计算

式中，Vsh为泥质含量，小数；当φ／Vsh＜0．26时，取φ／Vsh＝0．26，当计算的Swi≤0．15，取Swi＝0．15。

图7为××1井3种渗透率测井解释模型计算的效果图。图7中第6道φe为有效流动孔隙度，Swi为式（14）计算的束缚水饱和度。从图7中可以明显看出，Timur模型和 Wyllie－Rose模型计算的渗透率与岩心分析的渗透率比较普遍偏大，而本文提出的EREM渗透率模型计算的结果与岩心分析的结果比较吻合，证实了本方法的可靠性。

5 结 论

（1）依据电荷迁移与流体分子迁移相似性原理，推导出了有效流动孔隙度的表达式，认为有效流动孔隙度与对数下的渗透率具有很好的线性关系。

（2）利用四川盆地须家河组29块岩心实验数据，分别获取了EREM渗透率模型和 Wyllie－Rose渗透率模型中的固定参数，并利用已有的岩心数据对3种模型进行回判，结果EREM模型与岩心对比的结果优于Wyllie－Rose模型和Timur模型。

（3）将3种渗透率模型应用于实际井资料的处理，应用效果显示EREM渗透率模型在实际井资料中计算的结果明显优于其他2个模型，可以将该技术进行推广应用。

［1］张枫，王振升，马立军，等．一种检验试井解释有效渗透率合理性的方法［J］．天然气地球科学，2010，21（3）：367－370．

［2］安小平，李相方，程时清，等．不同方法获取渗透率的对比分析［J］．油气井测试，2005，14（5）：14－17．

［3］雍世和，张超谟．测井数据处理与综合解释［M］．东营：中国石油大学出版社，1996．

［4］Amaefule J O．Enhanced Reservoir Description：Using Core and Log Data to Identify Hydraulic（Flow）Units and Predict Permeability in Uncored Intervals Wells［C］∥ Formation Evaluation and Reservoir Geology Proceedings，SPE Annual Technical Conference and Exhibition，Omega SPE，Richardson X，USA，1996：295－304．

［5］袁新涛，彭仕宓，林承焰，等．分流动单元精确求取储层渗透率的方法［J］．石油学报，2005，26（6）：78－81．

［6］董春梅，林承焰，赵海朋，等．基于流动单元的测井储层参数解释模型［J］．测井技术，2006，30（5）：425－428．

［7］王月莲，宋新民．按流动单元建立测井储集层解释模型［J］．石油勘探与开发，2002，29（3）：53－54．

［8］Vander B M，Jutten C．Neural Networks in Geophysical Applications［J］．Geophysics，2000，65（4）：1032－1047．

［9］周金应，桂碧雯，李茂，等．基于岩控的人工神经网络在渗透率预测中的应用［J］．石油学报，2010，31（6）：985－988．

［10］夏宏泉，张贤辉，范翔宇，等．基于神经网络法的逐点渗透率测井解释研究［J］．西南石油学院学报，2001，23（1）：11－13．

［11］Wyllie M R J，Rose W D．Some Theoretical Considerations Related to the Quantitative Evaluation of the Physical Characteristics of Reservoir Rock from Electrical Log Data［J］．J Pet Tech，1950：189．

［12］Timur A．An Investigation of Permeability，Porosity，and Residual Water Saturation Relationship for Sandstone Reservoirs［J］．The Log Analyst，1968，July－Aug．

［13］Shang B Z，Jeffry G，Donald H．A Physical Model to Explain the First Archie Relationship and Beyond［C］∥SPE 84300，SPE Annual Technical Conference and Exhibition，Denver，Colorado，USA，2003，5－8October．

［14］Core Laboratories．“Worldwide Rock Catalog”，Integrated Reservoir Solutions Extranet［EB／OL］．https：∥core．corelab．com／irs version 2．6．

［15］Fang J H，Karr C L，Stanley D A．Genetic Algorithm and Its Application to Petrophysics［C］∥Society of Petroleum Engineers，SPE 26208，1992．