有色噪声对动态寻北的影响

蒋庆仙，白云超，王成宾

(西安测绘研究所，陕西西安710054)

一、引 言

陀螺寻北仪是一种采用陀螺仪作为角速率传感器快速精确测定真北方位的仪器。随着惯性技术、电子技术和计算机等技术的进步，陀螺寻北仪在车辆导航定位、海洋勘探、石油钻井、隧道开凿等领域均得到了日渐广泛的应用。根据采样和解算方式的不同，陀螺寻北仪有多种寻北方法。近年来兴起了动态旋转调制寻北法，在寻北过程中，惯性测量单元IMU(由陀螺仪和加速度计组成)绕其垂直中心轴连续转动，通过采样陀螺的输出信号解算出陀螺敏感轴的初始方位角［1-5］。其优点是通过连续转动使陀螺的常值漂移、随机漂移受到周期性调制，通过积分得到消除，因而可显著提高寻北精度。

在动态定位测量中，观测误差往往不属于高斯白噪声，而是具有一定时空相关性的有色噪声。有色噪声可看作是某一线性系统在白噪声驱动下的响应，它的存在严重影响着动态滤波的精度和可靠性，有必要在数据处理中加入有色噪声的检验和建模，以消除或减弱有色噪声对参数估计的影响。现已形成了多种减弱和消除有色噪声影响的方法，如附加有色参数滤波法、相邻观测值组差法、基于滤波残差建模法、自适应滤波和自适应抗差滤波［6-8］。在数据处理中常利用白噪声的定义与统计特性判断观测噪声是属于白噪声还是有色噪声。目前对有色噪声建模比较麻烦，常用的建模方法一般分为相关函数法和时间序列分析法，如AR模型、指数相关函数和高斯相关函数［9-10］。通过对有色噪声建模、拟合、预报，以及对观测值进行误差修正，使观测值中仅留下白噪声或近似于白噪声，从而减弱有色噪声对参数估计的影响。

为了分析有色噪声对动态寻北中方位角估值的影响，本文在一阶自回归AR模型的假设下推导了有色噪声对参数最小二乘估值的影响函数，分析了其影响性质。利用观测残差建立了有色噪声的一阶AR模型，并对有色噪声进行了拟合和预报［11］。为了削弱陀螺信号中异常噪声对寻北精度的影响，对陀螺信号进行了抗差估计以控制粗差的影响。计算结果表明，当陀螺信号中包含有色噪声时，采用一阶AR模型对有色噪声进行拟合和预报，能够有效削弱有色噪声的影响。采用一次启动漂移稳定性为0.03°/h的动调陀螺，在4 min之内系统寻北精度小于0.6'，远高于不考虑有色噪声影响得到的精度，极大地提高了系统的性能。

二、有色噪声对参数最小二乘估值的影响

设有观测序列 L1，L2，…，Ln，观测方程为

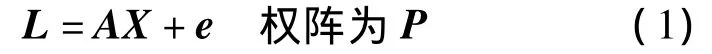
式中，X为参数向量;A为设计矩阵;e为真误差向量，其协方差矩阵为Σk。

当e为高斯白噪声序列时，参数的最小二乘(LS)解为［12］

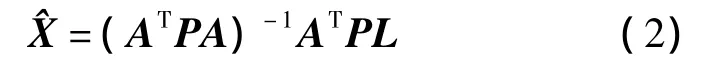
当e为有色噪声时，采用时间序列分析法描述有色噪声，即把平稳的有色噪声看做是由各时刻相关序列和各时刻出现的白噪声所组成。将tk时刻的有色噪声ek表示为［13］

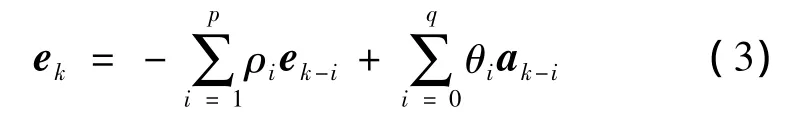
式中，ρi＜1(i=1，2，…，p)为自回归参数;θi＜1(i=1，2，…，q)为滑动平均参数;ak为白噪声，服从分布N(0，)。

式(3)称为自回归滑动平均ARMA(p，q)模型。模型前半部分称为自回归模型AR(p)，后半部分称为滑动平均模型MA(q)。

设有色噪声模型为一阶AR模型，k时刻的观测误差向量表示为

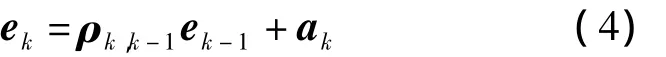
式中，ek-1为 k-1 历元的观测误差;ρk，k-1为相关系数矩阵;ak为高斯白噪声。将Lk修正为

则近似有

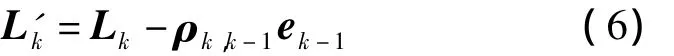
式中，L'k为经过有色噪声改正后的观测值。顾及式(2)可得参数最小二乘解为［9，11］

因而，有色观测噪声对参数解向量的影响函数(influence function，IF)为

由式(8)可见，纯有色噪声对参数最小二乘估计解的影响主要与观测误差、相关系数及设计矩阵有关。当加大观测的采样间隔时，其相关系数ρk，k-1必然减小，前面历元的观测误差对本历元参数估计的附加影响就小。当前一历元的观测精度很高，即ek-1很小时，有色噪声对参数估计的影响也将减小。

三、有色噪声的拟合与预报

1.有色噪声的拟合

当观测值中存在有色噪声时，利用观测残差在一阶自回归模型的基础上建立有色噪声模型。将k时刻的观测残差表示为

对于观测残差序列，有误差方程

当误差Δk服从正态分布时，有色噪声模型参数的最小二乘估值为

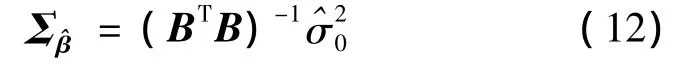
2.有色噪声的预报

有色噪声改进后，重写误差方程如下

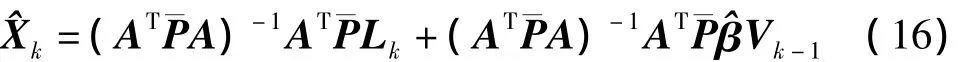
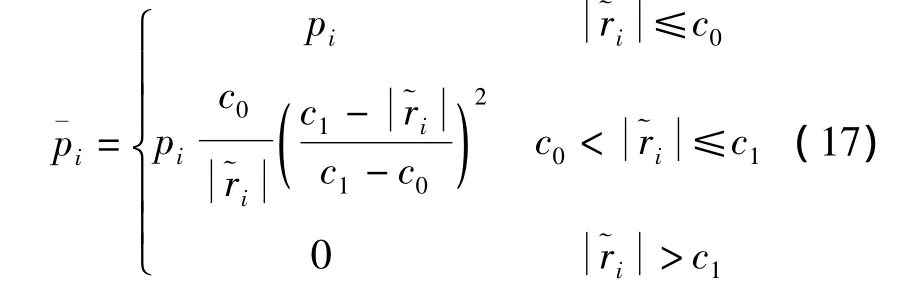
式(16)的解算一般采用迭代法，第k+1步的迭代解为

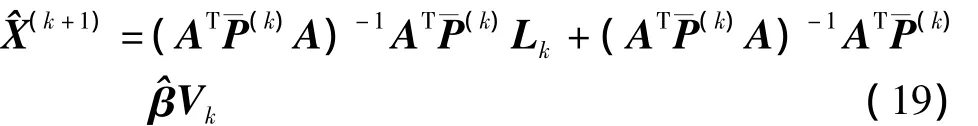
四、计算与分析

试验数据来自动调陀螺寻北仪，进行了7个测回的寻北试验。动调陀螺的一次启动漂移稳定性为0.03°/h。转台的转速设定为5 r/min，分别采集陀螺仪x、y轴的输出信号，采样率为25 kHz。采用高精度的锁相稳速控制电路使转台速率的相对稳定度达到10-4，DSP+FPGA构成了数据的高速采集与解算单元。

采用第1个测回的数据计算状态参数的初值，

在基于观测残差序列使用式(11)或式(13)获得AR模型的参数后，有色噪声的预报值可表达为［11］采用第2—7个测回的数据计算参数的估值并评定寻北精度。对测试数据采用以下5个方案处理，测值的权反映了每个测回的估值对本方案中方位角估值的贡献。抗差估计中迭代收敛的条件为，等价权函数的临界值c0、c1分别取为1.5和5。由于还没有得到方位角的实际值，计算中采用观测值的中误差考核寻北精度。表1给出各个方案中方位角的计算结果。

方案1:不考虑有色噪声影响的最小二乘估计;方案2:不考虑有色噪声影响的抗差估计;

方案3:对有色噪声进行最小二乘拟合的最小二乘估计;

方案4:对有色噪声进行最小二乘拟合的抗差估计。

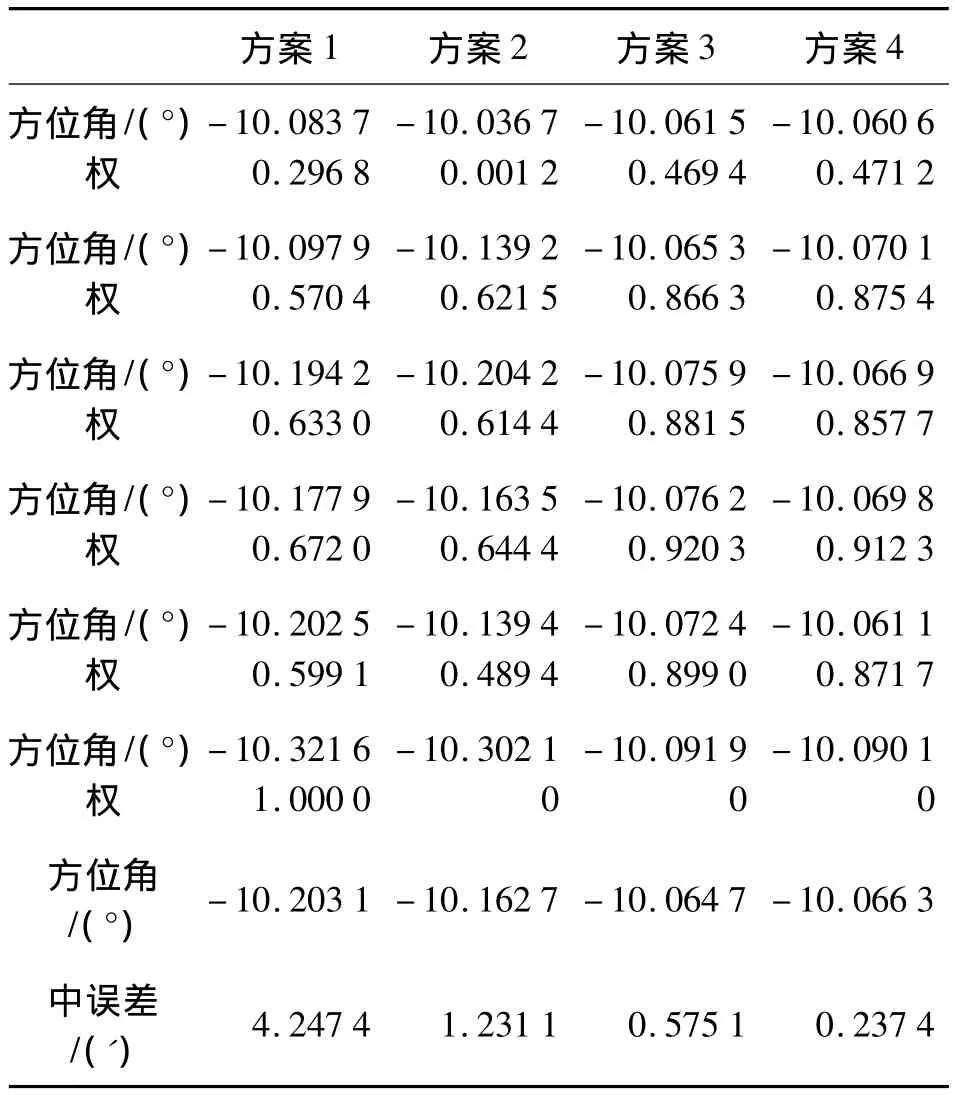
表1 寻北结果

为了直观显示有色噪声拟合的效果，由图1、图2分别给出观测值的原始残差和有色噪声拟合后的观测残差。由此可以看出原始残差的幅值为0.2°/h，而经过有色噪声拟合后的观测残差为0.1°/h。

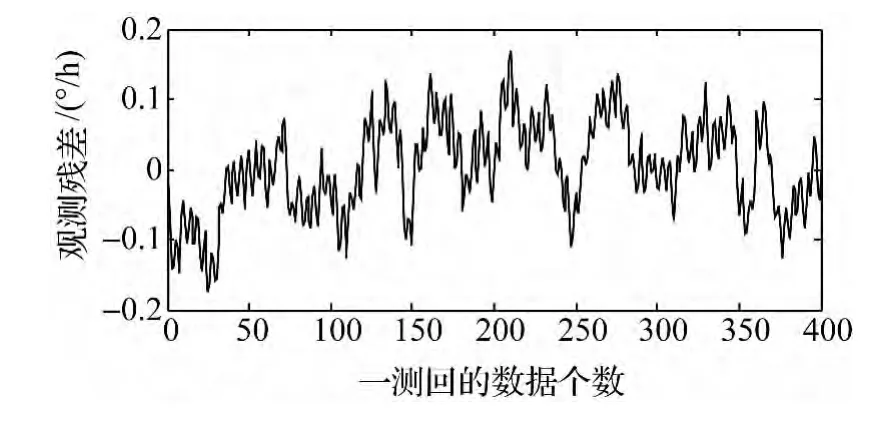
图1 原始残差

图2 有色噪声拟合后的残差

五、结 论

分析上述结果，可得如下结论:

1)陀螺仪信号中包含有色噪声时，动态寻北的精度和可靠性将受到严重的影响(见方案1的寻北结果)。

2)抗差估计能够削弱信号中存在的异常干扰的影响，并且可以将异常干扰剔除而不影响其余有用信号。算例中第6测回计算得到的方位角偏离了方位角的最终估值，但采用抗差估计时给予其零权处理，从而减弱了载体扰动对方位角估值的影响。

3)采用一阶自回归模型对有色噪声进行拟合和预报，能够有效削弱有色噪声的影响，极大地提高了系统的寻北精度(见方案3、方案4的寻北结果)。

4)最小二乘估计不具有抗差性，其控制粗差影响的能力要低于抗差估计。在采用最小二乘估计对有色噪声进行拟合和预报后，再进行抗差估计，获得了明显优于最小二乘估计的结果。

综上所述，有色噪声对参数估计的影响不容忽视，在动态寻北测量数据处理中，应充分考虑有色观测噪声的影响。当陀螺仪信号中包含有色噪声和异常干扰时，采用最小二乘估计对有色噪声进行拟合和预报，在此基础上进行抗差估计能够有效控制载体扰动和有色噪声两者的共同影响。

［1］KIM S J，LEE S S，KWON Y S.Dynamic North-finding Scheme Based on a Fiber Optic Gyroscope［C］∥Proceeding of SPIE.Orlando:SPIE，1997:126-136.

［2］KIM I S.KIM Y，Matisov A，et al.Dynamic Scheme North Finder Using a Fiber Optic Gyroscope［C］∥Proceeding of SPIE.Beijing:SPIE，1996:228-236.

［3］邹向阳，孙谦，陈家斌，等.连续旋转式寻北仪的寻北算法及信号处理［J］.北京理工大学学报，2004，24(9):804-807.

［4］徐建华，谢玲，高亚楠，等.旋转调制式寻北仪滤波技术研究［J］.北京理工大学学报，2005，25(8):718-721.

［5］张思将，秦石乔，王省书，等.连续旋转式激光陀螺寻北仪研究［J］.航空兵器，2006(1):12-15.

［6］赵长胜.有色噪声滤波理论与算法［M］.北京:测绘出版社，2011.

［7］崔先强.动态导航有色噪声的影响与控制［D］.郑州:信息工程大学，2003.

［8］崔先强，杨元喜，高为广.多种有色噪声自适应滤波算法的比较［J］.武汉大学学报:信息科学版，2006，31(8):731-735.

［9］杨元喜，崔先强.动态定位有色噪声影响函数——以一阶 AR 模型为例［J］.测绘学报，2003，32(1):6-10.

［10］吴富梅，杨元喜.顾及有色噪声的光纤陀螺信号的抗差谱分析［J］.测绘科学与工程，2006，26(3):50-53.

［11］杨元喜.自适应动态导航定位［M］.北京:测绘出版社，2006，178-185.

［12］杨元喜.抗差估计理论及其应用［M］.北京:八一出版社，1993.

［13］刘永红，范跃祖.激光陀螺漂移的非平稳随机信号建模［J］.战术导弹控制技术，2004，46(3):99-102.

［14］YANG Y.Robust Estimation of Geodetic Datum Transformation ［J］.Journal of Geodesy，1999，73(5):268-274.

［15］YANG Y，CHENG M K，SHUM CK，et al.Robust Estimation of Systematic Errors of Satellite Laser Range［J］.Journal of Geodesy，1999，73(7):345-349.