Mapgis软件网格化效果比较

刘 蕾

（中国冶金地质总局山东正元地质勘查院，济南 250101）

0 引言

Mapgis是绘制物探等值线图的常用软件之一，由它绘制的等值线图可包含点线面文件，易于在Mapgis下使用，可直接与地质、化探图件合成，与以往使用suffer绘制等值线后再通过文件转换生成Mapgis格式文件相比，简化了工作流程［1－5］。通过对不同网格化方法对比，确定了在物探等值线图绘制中距离幂函数反比加权法、Kring泛克立格网格化法是最佳的网格化方法。

1 Mapgis的4种网格化方法

等值线图的绘制是把离散的数据点向连续图形的变换处理，是建立在数学处理过程上的。因此，要用到插值和拟合方面的数据处理方法。在Mapgis中多采用距离幂函数反比加权法、Kring泛克立格法、稠密数据中值选取法和稠密数据高斯距离权法等4种数据插值方法，网格化后的数据绘制的等值线严格遵守固定不变的数学模型。

在Mapgis中也可以利用软件的绘图功能，引入传统的手工勾绘等值线方法，即考虑网格点周围的一两个数据的线性内插，它综合了技术人员的经验和区域性的地质认识，使代表地层性质的等值线图的误差变小。将Mapgis的4种网格化方法绘制的等值线与手工勾绘等值线进行对比，选择适合物探规则网数据的网格化模型。

1.1 距离幂函数反比加权法

设空间待插点为 P（xp，yp，zp），P 点邻域内有已知散乱点Qi（xi，yi，zi），i＝1，2，…，n。

利用距离幂函数加权反比法对P点的属性值Zp进行插值。其插值原理是待插点的属性值是待插点邻域内已知散乱点属性值的加权平均，权的大小和待插点及邻域内散乱点之间的距离有关，是距离的k（0≤k≤2）（k一般取2）次方的倒数。即：其中，di为待插点与其邻域内第i个点之间的距离［6］。

1.2 Kring泛克立格法

设研究区域为A，区域化变量（即欲研究的物理属性变量）为｛Z（x）∈A｝；x为空间位置（一维、二维或三维坐标）；Z（x）为在采样点xi（i＝1，2，…，n）处的属性值（或称为区域化变量的一次实现）Z（xi）（i＝1，2，…，n），则根据泛克立格插值原理，未采样点x0处的属性值Z（x0）估计值是n个已知采样点属性值的加权和，即：

式中，λi（i＝1，2，…，n）为待求权系数。

假设区域化变量Z（x）在整个研究区域内满足二阶平稳假设：

（1）Z（x）的数学期望存在且等于常数：E［Z（x）］＝m（常数）。

（2）Z（x）的协方差Cov（xi，xj）存在且只与两点之间的相对位置有关［2，6］。

1.3 稠密数据中值选取法

已知函数y＝f（x）在n＋1个点x0，x1，…，xn上的函数值yi＝f（xi），（i＝0，1，…，n），求一个多项式y＝P（x），使其满足P（xi）＝yi，（i＝0，1，…，n）。即要求该多项式的函数曲线要经过y＝f（x）上已知的n＋1个点（x0，y0），（x1，y1），…，（xn，yn），同时在其他x∈［a，b］上要估计误差R（x）＝f（x）－P（x）［7］。

1.4 稠密数据高斯距离权法

设F0（i，j）为分析区内网格点的要素值，（i，j）为各点行列序号，F（k）为测点实测要素值（k为测点序号），则插值公式

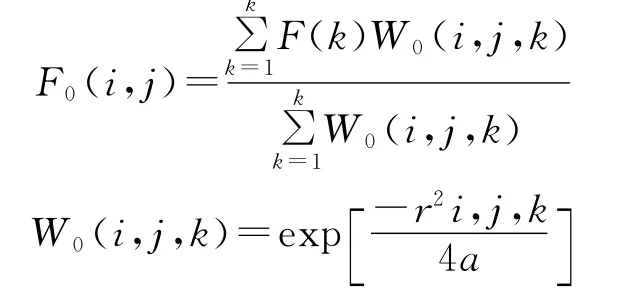
式中，ri，j，k是网格点（i，j）到k测点之间的距离；k为分析区和影响区半径内的测点总数；a为常数。

设F0（k）为用网格点上的插出值F0（i，j）反算出来的测点要素估计值。则用下式确定插值误差FD（k）。

式中，m，n为靠近测点k最近的网格点序号［8］。

2 Mapgis网格化方法的参数设定

网格间距、搜索方式是网格化时最重要的2个参数，关系到所派生数据的密度，并直接影响等值线模型的精度，最终影响物探异常的平面特征。

若网格间距过大，会丢失一些异常特征信息，也可能造成等值线扭曲，将使野外工作不能收到预期的效果。网格细分时，所绘等值线细节明显，最佳的网格间距以实际点线距进行设置较为合适。

搜索方式决定了网格化形成新的网格节点所使用的数据。搜索方式一般有4种：点搜索、简单搜索、象限搜索、卦限搜索。当数据分布比较均匀（测线无空点）时，可以使用所有的数据进行网格化，即不选择其搜索方式或选择默认值；当数据量增大，数据分布疏密不均（含有空点）时，须采用象限搜索或卦限搜索2种方式。

其他参数均可选择默认值。

3 Mapgis网格化方法应用效果比较

使用磁法观测的同一组ΔT数据以4种网格化方法建立的GRD数学模型进行离散数据网格化（网度100m×20m，无空点空线），采用高等级平滑等值线处理［9］，绘制了等值线图（图1）。以手工勾绘等值线图作为标准，与4种网格化方法绘制的等值线图进行对比（图2）。

图1 不同Mapgis网格化方法绘制的等值线图Fig.1 Contour map drawn with different Mapgis gridding methods

图2 不同网格化方法与手工绘制等值线图对比图Fig.2 Comparison of contour maps drawn with different Mapgis gridding methods to the hand drawing contour map

在网格化方法绘制的等值线图中，采用距离幂函数反比加权法和Kring泛克立格法绘制的等值线图完全重合，其等值线形态与手工勾绘等值线形态相近；稠密数据高斯距离权法与手工勾绘等值线有约10%的离差，局部的等值线异常形态变化较大；稠密数据中值选取法与手工勾绘等值线图相比，异常中心沿水平方向偏离约100m，沿垂直方向偏离约40m，误差较大，这是因为稠密数据中值选取法采用多项式函数曲线拟合，其误差是由函数引起的，因而带来了不易估计的误差范围。Kring泛克立格法［10］是以最优加权组合预测方法为基础，其权重决定其精度，可以控制其预测误差在较小的范围内，因此与手工勾绘等值线图的误差较小。

4 结论

通过对比分析，Kring泛克立格法、距离幂函数反比加权法和手绘等值线ΔT异常形态相似。无论从总体上，还是局部等值线细节上，Kring泛克立格法、距离幂函数反比加权法都要比稠密数据中值选取法、稠密数据高斯距离权法精度高，等值线绘制合理。因此，在物探等值线绘制时可选择Kring泛克立格法或距离幂函数反比加权法网格化方法。同时，本次网格化方法对比采用的是物探规则网数据，即物探数据分布在测线网度100m×20m中，没有空点、空线，在网格化参数设置时均选其默认值。从等值线细节形态来看，手绘等值线和Kring泛克立格法、距离幂函数反比加权法还是存在一些偏差，原因是手绘等值线是综合地质认知勾绘出来的，而Kring泛克立格法、距离幂函数反比加权法是以数据建立模型，只考虑了算法因素，同时受网格化时所选参数的合理性制约，二者之间的调整还需要进一步的研究确定。

［1］黄健全，罗明高，胡雪涛.实用计算机地质制图［M］.北京：地质出版社，1998.

［2］王家华，高海余，周叶.克里金地质绘图技术——计算机的模型和算法［M］.北京：石油工业出版社，1999.

［3］孟小红，王卫民，姚长利，等.地质模型计算机辅助设计原理与应用［M］.北京：地质出版社，2001.

［4］胡有元，黄杏元.计算机地图制图［M］.北京：测绘出版社，1987.

［5］邬伦，刘瑜，张晶，等.地理信息系统：原理、方法和应用［M］.北京：科学出版社，2001：7－12.

［6］靳国栋，刘衍聪，牛文杰.距离加权反比插值法和克里金插值法的比较［J］.长春工业大学学报，2003，24（3）：53－57.

［7］李庆杨.数值分析：第5版［M］.北京：清华大学出版社，2008.

［8］杨昌军，陈渭民，罗玲，等.高斯权重法在温度场插值中的应用研究［J］.南京气象学院学报，2004，27（5）：606－615.

［9］姜启源.数学模型［M］.北京：高等教育出版社，1987.

［10］周叶，王家华.一种分块连续曲面的克里格估计方法［C］∥中国地质学会数学地质专业委员会.中国数学地质：5.北京：地质出版社，1994.