基于二阶双渐近法的双层圆柱壳在水下爆炸作用下的鞭状运动＊

刘云龙，汪 玉，张阿漫

（1.武汉第二船舶设计研究所，湖北 武汉 430205；2.哈尔滨工程大学船舶工程学院，黑龙江 哈尔滨150001；3.中国人民解放军92857部队，北京100161）

圆柱壳作为潜艇典型的结构形式，常被用作潜艇结构强度机理性研究的对象。在很多情况下对圆柱壳结构抗冲击性能深入研究的成果可以推广到实际潜艇上。因此，本文中以双层圆柱壳结构为研究对象，对水下爆炸载荷下圆柱壳结构的鞭状运动特性进行分析，旨在为潜艇抗冲击设计和研究提供参考。水下爆炸问题具有瞬态强非线性特点，其涉及的流固耦合问题一直是舰船抗冲击研究的热点和难点。早在20世纪60年代，研究人员就尝试通过解析的方法求解一些简单的冲击问题。比较有代表性的是H.Huang等早期的工作，其中得到了一些球壳以及圆柱壳等简单结构在平面阶跃波［1－2］及球面波［3］作用下的弹性响应。尽管此类方法对于实际复杂结构并不适用，但在后来的研究中通常用来验证理论和数值模型的精度和有效性。随着计算机性能的提高和边界元的发展，流固耦合问题的数值求解技术得到了很大的提高。对现代水下冲击流固耦合研究影响较大的是T.L.Geers在1971年提出的双渐近（double asymptotic approximation，DAA）法［4］。该方法分别采用平面波假设和势流假设对水下冲击问题的前期和后期响应进行近似，而中间频段则通对两者进行匹配得到。随后的研究中，T.L.Geers［5］对DAA法［4］进行了改进，考虑了结构曲率的影响以及前后期的非线性匹配问题，形成了二阶双渐近（second－order doubly－asymptotic approximation，DAA2）法。DAA2法已被广泛应用于水下冲击防护研究。针对潜艇结构声学覆盖层问题，刘建湖［6］对DAA2法进行改进，考虑波在声学覆盖层中的反射和透射特性，将该过程分为声学反射阶段和DAA2阶段分别求解，发现用传统DAA2法处理声学覆盖层问题时低估了冲击波载荷的作用。随后，孙士丽［7］、王诗平等［8］通过计入非线性的二阶速度项，对DAA2法进行进一步改进，得到了非线性双渐近（non－linear second－order doubly－asymptotic approximation，NDAA2）法。宗智等［9］结合DAA2法和有限元法，计算了气泡脉动载荷下简单船体结构的动态响应和应力集中现象。董海等［10］针对潜艇的鞭状运动问题，将DAA2法和船体梁模型结合在一起，采用DAA2法计算流体载荷，用变截面梁模型计算结构响应，对结构的时域和频域响应均进行了深入分析。然而，由于DAA2方程是基于无限域三维波动方程推导的，因此对内流场问题不适用。尽管M.A.Sprague等、T.L.Geers等对经典DAA2法进行修改并推广到内域问题11－13，但在实际计算中经典DAA2法仍有较多限制。因此，本文中对双层圆柱壳结构舷间水对应的内流场采用声固耦合求解，而对外流场采用DAA2法求解，两者在非耐压壳处耦合，形成适用于双层圆柱壳结构的流固耦合分析方法，并据此分析水下爆炸载荷下双层圆柱壳结构的鞭状运动特性。

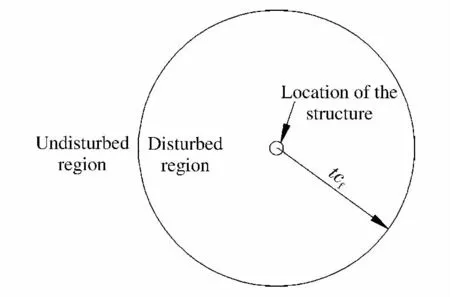
图1 DAA2法后期时域近似示意图Fig.1 Scheme of later approximation in time domain of DAA2

1 理论和数值模型

1.1 双渐近法理论模型

关于DAA2法，对前期近似采用在平面波假设下的流固耦合模型。在该假设下，任意时刻时边界上的流体动压力不受附近其他点的影响，推导过程相对简单，本文不再赘述。对后期近似，有不同的推导方法。王诗平等［14］通过将延迟积分方程进行拉普拉斯变换，并在拉氏空间内对方程进行简化，最后通过拉氏逆变换变回时域空间，为DAA2法提供了新的切入点。采用常规格林函数法，重新推导DAA2法后期近似公式。该推导方法更简便，物理意义更明确，旨在为DAA2法后续研究提供新的视角。假设流场速度势φ满足波动方程：

式中：cf为流体中的声速。若取格林函数，则有：

式中：R＝p－q为流场中从源点q指向场点p的矢量。于是，令式（1）×G－式（2）×φ，得：

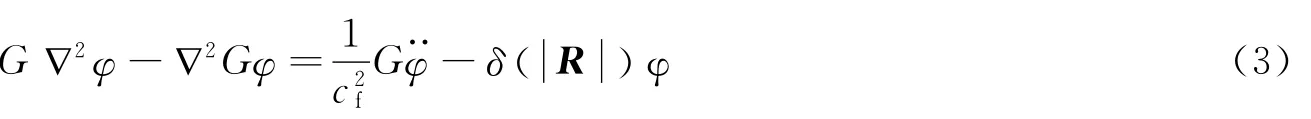
对式（3）在整个流域V内积分并应用格林第2公式可得：

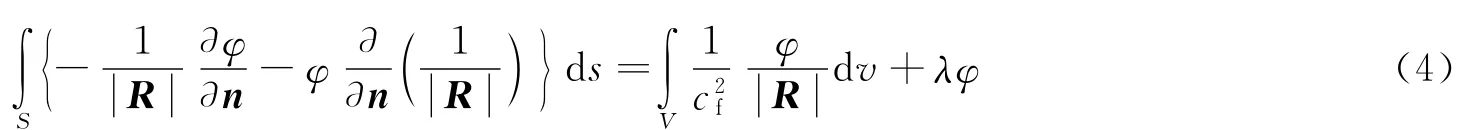
式中：S为流场V的边界，n为其单位法向量。式（4）即为求解波动方程的DBEM（domain boundary element method）积分方程。对式（4）左端积分，可采用常规边界元法离散实现，而右侧体积分项，由于积分域是自由场中的无界空间，只能进行近似。根据DAA2法的思想，考虑t cf≫L时对方程进行近似，其中L为结构的特征尺度，此时被结构扰动的流场可认为是一个半径为t cf的球体，结构的影响可看作球体中心的点源和偶极子的贡献。由于点源和偶极子的诱导速度势分别按照进行衰减，因此略去偶极子影响所产生的二阶项，结构对流场的贡献相当于球体中心一个点源的影响。于是根据波动方程三维空间的时域基本解，流场中任意点的速度势可以近似表示为：

式中：m （t）为源强的任意函数。于是式（4）右端的体积分可化为：

式中：C为待定常数。为确定C的取值，将其化为积分形式代入式（4），当t＝0时，显然C＝0。记u·n＝将式（6）代入式（4），有：

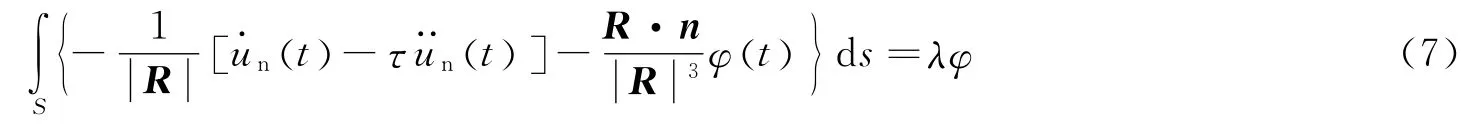
可见式（7）即为DAA2后期近似积分方程。通过平面波假设，冲击问题的前期近似可表示为［5，14］：

式中：χ为边界的局部曲率。将前期近似和后期近似在频域内匹配，整理可得DAA2边界积分方程［5，14］：

1.2 水下爆炸载荷

水下爆炸气泡脉动是一个强非线性的物理化学过程，针对不同的问题已提出了很多气泡模型。其中T.L.Geers等基于DAA2法提出的单个水下爆炸气泡脉动模型［15］考虑了流场的可压缩性和气泡内部气体的声学特性，因此在气泡各次脉动过程中，能够真实反映气泡最大半径和气泡脉动压力峰值的衰减。另外考虑了气泡中心的上浮，并通过以往水下爆炸气泡实验数据对上浮中的阻力进行了匹配，得到结果与实验结果吻合良好。在随后的研究中，T.L.Geers等对Geers－Hunter模型进行了一些优化调整［16］。采用Geers－Hunter模型计算得到气泡的脉动和迁移运动后，则可通过以下方法计算流体中任意一点的流体速度势［17］：

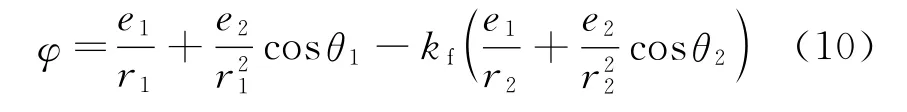
图2 水下爆炸气泡脉动载荷计算示意图Fig.2 Scheme of the calculation of underwater explosion bubble pulsation load

式中：右侧第1项为气泡脉动等效的点源所诱导的速度势，第2项为气泡迁移等效的偶极子所诱导的速度势，后面2项为自由面镜像的气泡所诱导的速度势。其中e1和e2分别为源强和偶极子强度；kf为自由面的反射因数，由于本文中分析深水中结构对水下爆炸的动态响应，因此不考虑自由面影响，kf取值为0；r1和r2分别为气泡中心和镜像气泡中心的距离；θ1和θ2分别为2连线与铅垂线的夹角，见图2。

然后通过非定常伯努利方程得到流场任意位置压力。气泡等效的变强度点源和偶极子强度需要满足气泡表面的连续性条件，可分别表示为：

式中：a为气泡等效半径，vm为气泡垂向迁移速度，d为水深。

1.3 BEM与FEM耦合接口

对FEM（finite element method）求解器选择ABAQUS／Explicit，可通过时间显式积分的方法计算结构在外载荷作用下的响应。由于不需要迭代过程，计算一般不存在收敛性问题，而时间积分的误差对于爆炸冲击这种瞬态分析来讲通常为小量，不会对结果产生明显影响。

图3中的数字表示时间增量步，在同一个时间增量步中，FEM计算得到的结构变形、速度以及加速度通过接口程序传递到BEM程序中，然后根据DAA2法计算得到结构湿表面的流体动压力，并在下一个时间增量步中传递给ABAQUS的FEM求解器，更新FEM中的载荷。重复以上流程，实现BEM和FEM之间的数据传递和沿时间的显式推进。

图3 ABAQUS用户子程序数据流示意图Fig.3 Data flow in the user－subroutine of ABAQUS

FEM同BEM的数据传递过程中存在一个延迟问题，即FEM求解器在计算时采用的是上一个时间增量步的压力数据，对此可采用前2个增量步的载荷数据外插的方法得到当前增量步的载荷：

式中：下标表示增量步数。对于BEM和FEM间的数据传递过程，本文中采用非共节点的网格映射方法，一方面减小BEM的计算规模，另一方面尽可能地保持较高的精度。

2 计算结果分析与讨论

2.1 数值模型精度验证

通过和P.Zhang等［18］针对充水球壳经典算例推导的解析解进行对比，验证本文计算模型的有效性。该算例旨在考察厚度为1mm、内部充满水的弹性钢质球壳在1MPa平面阶跃波作用下的响应。

图4为不同时刻球壳内流场的声压云图。从图4可知：在相互作用初期，内流场透射冲击波幅值与入射波基本一致，且波阵面以平面向前推进；随着时间的增加，由于结构中应力波的波速大于流场波速，因此远离壳体的球壳中部的冲击波明显慢于外侧靠近球壳部分流体，从而使波阵面不再保持平面，见图4（b）；当透射波到达球壳下部时，又产生了一定的反射，透射压力叠加，形成高压区，见图4（c）和（d）。

图4 不同时刻内流场声压云图Fig.4 Acoustic pressure of the inner field at different times

图5分别是不同方法计算结果中球壳上迎爆点和背爆点在冲击波方向的速度对比。可以看到，在图5（a）中内外域均为ABAQUS／声固耦合计算结果的高频部分衰减过快，因此在后期的速度曲线较光滑。在图5（b）中，背爆点产生了2次明显的加速过程：第1次发生在t＝0.6ms左右，为应力波通过壳体传递到背爆面所致；第2次发生在t＝1.3ms左右，为内流场透射压力到达背爆面所致。3种方法的计算结果基本一致，表明本文中所建立的计算模型可用于水下冲击问题的工程和理论研究。

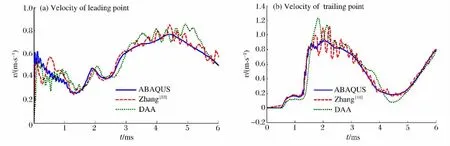
图5 数值模型对比验证Fig.5 Comparison among different methods

2.2 圆柱壳结构总体响应特性研究

计算模型如图6～7所示。计算模型长约75m，非耐压壳直径约8m，耐压壳直径约6m，肋距0.6m，一阶湿模态频率约为2.6Hz。对外流场采用DAA2法模拟，对内流场采用声固耦合法模拟，两者在非耐压壳处满足连续性条件。由冲击动力学和结构动力学的相关理论可知，舷间流场的存在并未改变细长圆柱壳的纵向体质量和刚度的分布情况，因此对总体低阶振动特性不会产生明显影响。但舷间流场对高频冲击波的透射作用会显著改变结构的局部高频响应特征，尤其是前期冲击波作用阶段更明显。

图6 双层圆柱壳总体响应计算示意图Fig.6 Configuration of the total response simulation of double cylindrical structure

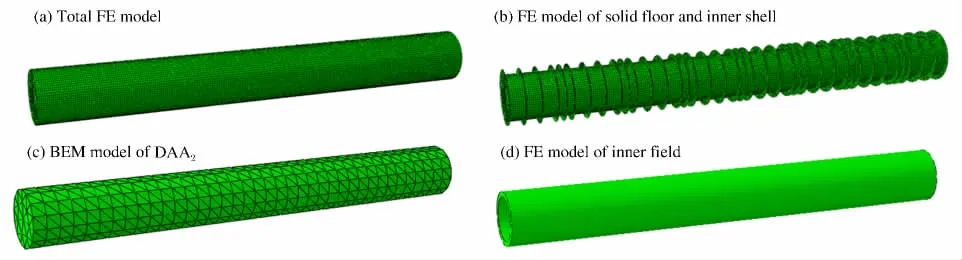
图7 双层圆柱壳计算模型Fig.7 Calculation models for double cylindrical shell structures

对舰艇在水下爆炸作用下的总体响应已进行了大量的理论和实验研究，通常认为当气泡脉动频率接近或略小于舰艇一阶模态频率，即气泡脉动周期略大于结构固有周期时，鞭状总体响应最明显。气泡脉动周期可通过库尔估算公式获得［1］：

式中：K 为材料常数，对于 TNT，K≈2.11s·kg－1／3·m5／6；W 为装药质量，kg；d 为水深，m；10.3m 为大气压对应的压力水头。

为了深入研究不同工况参数对鞭状运动的影响，定义周期参数γT＝Tb／Ts和爆距参数γR＝R／L，作为衡量水下爆炸气泡诱导鞭状运动的量纲一参量。Tb为气泡脉动周期，可通过式（14）计算；Ts为结构一阶湿模态对应的固有频率；R为爆距；L为结构特征长度，对加筋圆柱壳，本文中L取壳体长度。

2.2.1 周期比的影响

首先考虑周期参数对鞭状运动的影响，工况设置见表1，其中TNT炸药质量均为1t，爆距均为20m，来分析不同水深d对鞭状运动的影响。事实上，方位角对结构鞭状运动的影响：一方面，体现在气泡向上迁移时不同方位角下的爆距改变趋势不同；另一方面，则是由于气泡迁移引起的流场非对称性导致的。方位角为90°时气泡向上迁移对结构鞭状运动响应影响最小。因此，为减少变量数量，本文的分析均是针对方位角为90°的情况。

表1 柱壳总体响应工况设置Table 1 Case parameters for total responses of cylindrical shell structures

由于鞭状运动主要是一阶模态形式下的运动，因此采用船体梁中点挠度来评估圆柱壳鞭状运动的幅值。考虑到圆柱壳在冲击载荷下产生的刚体位移，将圆柱壳挠度定义为：

式中：Uc为圆柱壳中部的垂向位移；Ul和Ur分别为圆柱壳两端的垂向位移。

先以工况1为例，圆柱壳到达鞭状运动幅值各波峰波谷时的变形和应力云图如图8所示。

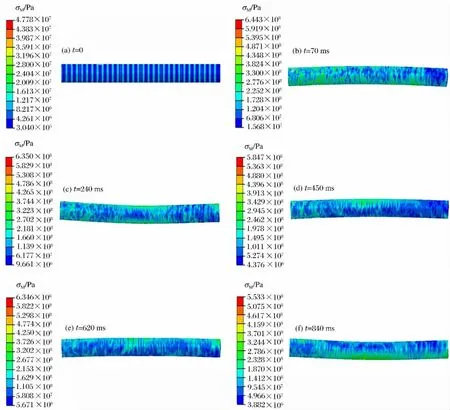
图8 工况1鞭状运动应力云图Fig.8 Mises stress contours of the whipping response in case 1

在工况1下，质量为1t的TNT在水下60m深处爆炸的气泡一次脉动周期为610ms，约为圆柱壳结构一阶固有周期的1.60倍。从图8可以看出，工况1的圆柱壳在水下爆炸的前期的冲击波作用下已被激起了一阶鞭状运动，但幅值不大。而鞭状运动过程中在240和450ms出现了2个相邻的波峰，间隔时间较短，3个鞭状运动幅值没有明显增大。

图9 工况1鞭状运动幅值和冲击载荷曲线Fig.9 Curves of whipping response to shock pressure in case 1

图9为工况1中鞭状运动幅值和冲击载荷曲线。其中，绿虚线为冲击波和气泡脉动载荷，实线为计算得到的三维圆柱壳结构的鞭状运动幅值曲线。该工况下结构最大幅值仅有0.1m左右；另外，在第2次鞭状运动周期出现2个紧邻的波峰。当冲击波载荷过后，圆柱壳开始第1次鞭状运动，并很快达到第1个波峰。在回落过程中，受气泡脉动载荷负压区的作用，对圆柱壳结构输入了较大的能量，使第1个鞭状运动波谷的幅值大于第1个波峰的幅值，约为0.17m。由于工况1的气泡脉动周期较长，当圆柱壳结构第2个鞭状运动峰值出现时，气泡一次脉动压力尚未到来，因此在这段时间内，圆柱壳的鞭状运动主要是由本身的有阻尼震荡和脉动压力的负压区共同主导的，幅值仅有0.10m，较第1个波谷有明显的减小。气泡一次脉动载荷峰值在鞭状运动第2个波峰的回落过程中出现，从而使结构调转运动方向，形成了另一个波峰。在这种水深较小的工况下，气泡脉动周期较长，使气泡一次脉动压力峰值到来的相对较晚，若恰巧出现在鞭状运动的回落阶段，则会产生类似的鞭状运动的双峰现象，即存在2个间隔很小的波峰。在这种情况下，通常不会引起剧烈的鞭状运动。

对于工况3，1t的TNT在水下80m深处爆炸的气泡一次脉动周期为490ms，约为圆柱壳结构一阶湿模态对应的周期的1.3倍。工况3鞭状运动幅值和冲击载荷时历曲线见图10。

图10 工况2鞭状运动幅值和冲击载荷曲线Fig.10 Curves of whipping response to shock pressure in case 2

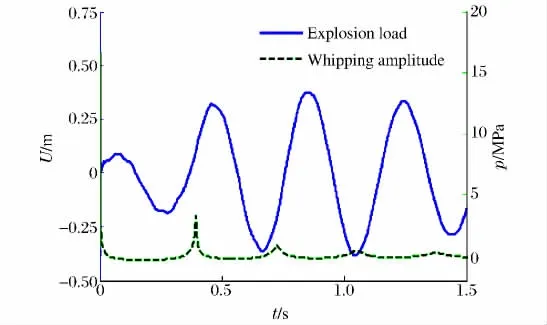
图11 工况5鞭状运动幅值和冲击载荷曲线Fig.11 Curves of whipping response to shock pressure in case 5

从图10可看出：与工况1相同，在从第1个波峰回落的过程中，由于同时受到气泡脉动载荷负压区的能量输入，使第1个鞭状运动波谷的幅值大于第1个波峰的幅值；而气泡一次脉动载荷又恰好位于鞭状运动的第2次上升阶段，同样以做正功的形式向圆柱壳结构输入能量，使鞭状运动幅值继续增大，达到0.28m；在接下来的第3和第4个周期中，气泡脉动载荷同样为系统输送能量，从而使峰值逐个增大，分别达到0.35和0.41m；而第5个周期时，脉动压力已经衰减到很小，所做的功不足以抵消整个系统的能量耗散，使鞭状运动幅值开始回落。

在工况5中，周期参数约为1.1，所对应圆柱壳鞭状运动最大幅值仅有0.37m，远小于工况3。图11中共有2个气泡脉动压力峰值出现在鞭状运动上升阶段，鞭状运动最大运动幅值出现在第3个运动周期。第1个周期的波峰同样来自冲击波载荷，气泡前2次脉动压力峰值均在鞭状运动上升阶段，使运动幅值逐次增加。而气泡第3次脉动压力峰值刚好处于圆柱壳鞭状运动第3个波谷，此时鞭状运动速度为零，即此次气泡脉动载荷基本对系统不做功。同时由于系统能量的耗散，使第4次的运动幅值开始减小。随后的气泡脉动压力峰值开始出现在结构鞭状运动的下降阶段，从而加快了鞭状运动衰减的速度。从图12可知，随着水深的增大，圆柱壳结构鞭状运动周期逐渐减小。综合所有工况，分析周期比与鞭状运动最大幅值Um的关系，将其绘于图13。

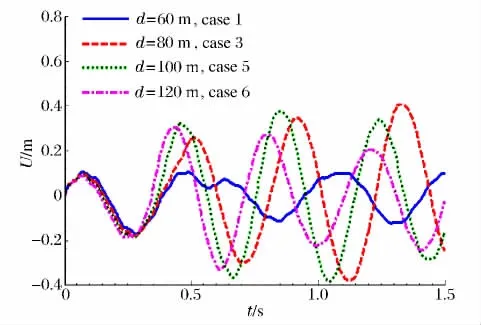
图12 不同工况下，鞭状运动时历曲线Fig.12 Whipping response curves in different cases

图13 鞭状运动最大幅值随周期比的变化Fig.13 The maximum amplitude of the whipping response varied with period ratio

从图13可知，随着周期比的增大，鞭状运动幅值逐渐增大，水深为80～90m，即1.19＜γT＜1.30时，鞭状运动幅值达到最大，随后迅速衰减。综合以上分析可知，当1.19＜γT＜1.30时，可是使连续多个气泡脉动峰值出现在圆柱壳鞭状运动幅值的上升阶段，从而连续向系统输送能量，达到共振。当γT从1.19减小时，气泡脉动峰值处于鞭状运动上升阶段的个数逐渐减小，从而使鞭状运动最大幅值随之减小。当γT从1.30增大时，气泡第一次脉动峰值直接后移至鞭状运动幅值下降阶段，对系统的能量输入变为负，在鞭状运动的第2个峰值附近紧接着出现第3个峰值，从而使鞭状运动最大幅值迅速减小。

2.2.2 爆距比的影响

除水深外，爆距也会明显影响鞭状运动的形式和幅值。为分析爆距对圆柱壳结构鞭状运动的影响，进行一系列的计算，工况设置见表2，TNT炸药的质量均为1t，水深均为80m，气泡脉动周期为490ms。不同工况下圆柱壳鞭状运动的幅值曲线见图14～15。从图14～15可知：随着爆距的增大，鞭状运动幅值迅速减小。其次，爆距越小的工况，鞭状运动第1个周期越长，如R＝10m的工况第1个鞭状运动周期约为550ms，超过圆柱壳结构固有周期380ms约45%，因此使后续周期相对于其他工况后延了约1／4个周期。而对于R≥20m的工况，鞭状运动每个周期的长度基本都是均匀的。图14给出了80m水深下各工况最大鞭状运动幅值随爆距的变化趋势。从图14可以看出，随着爆距的增大，圆柱壳结构鞭状运动幅值迅速减小。这种减小一方面来自于水下爆炸载荷随爆距的倒数关系，另一方面则是随着爆距的增大，爆炸载荷在结构纵向的分布逐渐均匀，使结构更多倾向于刚体平动，而非鞭状运动形式的弯曲响应。

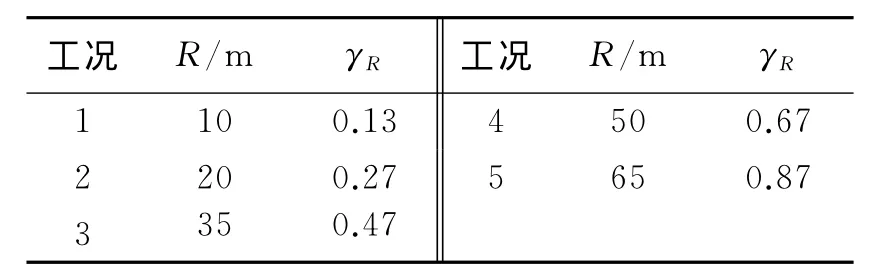
表2 柱壳总体响应工况设置Table 2 Case parameters for total response

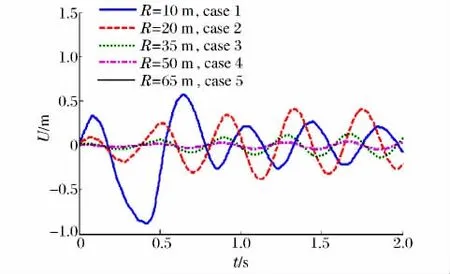
图14 爆距对鞭状运动幅值的影响Fig.14 Effect of explosion distance on the amplitude of the whipping response

图15 鞭状运动最大幅值随爆距比的变化Fig.15 The maximum amplitude of the whipping response varied with explosion distance ratio

3 结 论

从波动方程出发，推导了DAA2法的后期近似，并结合声固耦合法初步解决了双层圆柱壳内流场问题，采用ABAQUS接口耦合实现了圆柱壳水下爆炸冲击响应的计算分析。通过简单算例的验证表明，本文中建立的数值模型可用于圆柱壳水下冲击的工程和理论研究。据此分析了双层圆柱壳结构在水下爆炸载荷下的总体响应特性，发现对于本研究的参数范围，周期比为1.2到1.3之间时，能够诱发最严重的鞭状运动；当周期比从1.2减小时，鞭状运动幅值逐渐减小；而当周期比从1.3增大时，鞭状运动幅值迅速减小；圆柱壳结构鞭状运动幅值随爆距的增加呈平方关系减小。

［1］Huang H.Transient interaction of acoustic plane waves with a spherical elastic shell［J］.The Journal of the Acoustical Society of America，1969，45（3）：661－670.

［2］Huang H.An exact Analysis of the transient interaction of acoustic plane waves with a cylindrical elastic shell［J］.Journal of Applied Mechanics，1970，37：1091－1099.

［3］Huang H，Lu Y P，Wang Y F.Transient interaction of spherical acoustic waves and a spherical elastic shell［J］.Journal of Applied Mechanics，1971，38：71－74.

［4］Geers T L.Residual potential and approximate methods for three－dimensional fluid－structure interaction problems［J］.Journal of the Acoustical Society of America，1971，49（5B）：1505－1510.

［5］Geers T L.Doubly asymptotic approximations for transient motions of submerged structures［J］.Journal of the A－coustical Society of America，1978，64（5）：1500－1508.

［6］刘建湖.舰船非接触水下爆炸动力学的理论与应用［D］.无锡：中国船舶科学技术研究所，2002：89－112.

［7］孙士丽.瞬态载荷作用下大幅运动航行体流固耦合方法及应用研究［D］.哈尔滨：哈尔滨工程大学，2009：15－34.

［8］王诗平，孙士丽，张阿漫，等.冲击波和气泡作用下舰船结构动态响应的数值模拟［J］.爆炸与冲击，2011，31（4）：367－372.Wang Shi－ping，Sun Shi－li，Zhang A－man，et al.Numerical simulation of dynamic response of warship structures subjected to underwater explosion shockwaves and bubbles［J］.Explosion and Shock Waves，2011，31（4）：367－372.

［9］张弩，宗智，张文鹏，等.基于双渐进方法的水下爆炸气泡载荷作用下舰船的动态响应分析［J］.振动与冲击，2012，32（23）：50－56.Zhang Nu，Zong Zhi，Zhang Wen－peng，et al.Dynamic response of a ship hull structure subjected to an underwater explosion bubble based on doubly asymptotic approximation method［J］.Journal of Vibration and Shock，2012，32（23）：50－56.

［10］董海，刘建湖，吴有生.水下爆炸气泡脉动作用下细长加筋圆柱壳的鞭状响应分析［J］.船舶力学，2007，11（2）：250－258.Dong Hai，Liu Jian－hu，Wu You－sheng.Whipping response analysis of slender stiffened cylindrical shell subjected to underwater explosion with bubble pulse［J］.Journal of Ship Mechanics，2007，11（2）：250－258.

［11］Geers T L，Hunter K S.An integrated wave－effects model for an underwater explosion bubble［J］.The Journal of the Acoustical Society of America，2002，111（4）：1584－1601.

［12］Geers T L，Park C K.Optimization of the G ＆ H bubble model［J］.Shock and Vibration，2005，12（1）：3－8.

［13］Sprague M A，Geers T L.Response of empty and fluid－filled submerged spherical shells to plane and spherical，step－exponential acoustic waves［J］.Shock and Vibration，1999，6：147－157.

［14］王诗平，孙士丽，张阿漫，等.可压缩流场中气泡脉动数值模拟［J］.力学学报，2012，44（3）：513－519.Wang Shi－ping，Sun Shi－li，Zhang A－man，et al.Numerical simulation of bubble dynamics in compressible fluid［J］.Journal of Theoretical and Applied Mechanics，2012，44（3）：513－519.

［15］Geers T L，Zhang P Z.Doubly asymptotic approximations for submerged structures with internal fluid volumes：Formulation［J］.Journal of Applied Mechanics，1994，61（4）：893－899.

［16］Geers T L，Zhang P Z.Doubly asymptotic approximations for submerged structures with internal fluid volumes：Evaluation［J］.Journal of Applied Mechanics，1994，61（4）：900－906.

［17］Wilkerson S A.Elastic whipping response of ships to an underwater explosion loading［D］.Washington：George Washington University，1985：57－72.

［18］Zhang P，Geers T L.Excitation of a fluid－filled，submerged elastic shell by a transient acoustic wave［J］.Journal of the Acoustical Society of America，1993，93（2）：696－705.