双驴头抽油机后驴头型面设计的数值分析方法

许冯平，赵志聪，周 延

（东北石油大学 机械科学与工程学院，黑龙江 大庆163318）

双驴头抽油机后驴头型面设计的数值分析方法

许冯平，赵志聪，周 延

（东北石油大学 机械科学与工程学院，黑龙江 大庆163318）

后驴头的型面对双驴头抽油机的性能有很大的影响，须进行优化设计才能实现精确平衡，达到节能降耗的目的。针对后驴头型面为阿基米德螺线的双驴头抽油机设计模型中复杂的超越方程解析求解的困难，结合MATLAB的函数，编制相应的M文件，给出一种数值分析方法，进行一阶导数和二阶导数的运算，从而进行抽油机运动分析和动力分析，完成优化设计。该数值分析方法简单易行，以差分代替微分运算，为双驴头抽油机的性能分析提供了数值分析手段。运算精度足以满足工程设计的要求。

双驴头抽油机；阿基米德螺旋线；数值分析

双驴头抽油机的实质是将常规型游梁抽油机的定尺度曲柄连杆机构衍变为变尺度曲柄连杆机构，用驱动绳代替了连杆的硬连接。曲柄连杆机构的尺度变化有利于提高抽油机的性能［1-6］。由于作为连杆的是钢丝绳，它始终与后驴头型面相切，所以双驴头抽油机的传动角很大，接近于90°，具有很好的动力性能。同时，游梁后臂的有效长度随曲柄转角变化而变化，当悬点载荷较大时，游梁后臂有效长度变大，这使得曲柄转矩不致过大；当悬点载荷较小时，游梁后臂有效长度变小，使曲柄转矩不致过小。其变尺度性也改变了抽油机的转矩因数的变化规律，使其近似按正弦曲线规律变化，从而使曲柄上的净转矩比较稳定，波动小，也不产生负转矩。因而，双驴头抽油机降低了净转矩值，得到了更好的平衡效果，降低了能耗和整机的质量，有利于提高冲程。已在大庆油田、华北油田等得到了广泛应用［7］。

但在使用中，双驴头抽油机还是存在不尽如人意之处，例如，后悬绳易断，不能精确平衡，不易适应多种区块的要求等。后悬绳易断、平衡效果和转矩因数的变化规律都与后驴头的型面曲线有很大关系，研究表明：已有的3种后驴头型面曲线，阿基米德螺旋线，三圆弧和渐开线，以阿基米德螺旋线的精确平衡效果最好，转矩因数几乎为正弦曲线［8-10］。

但对于后驴头型面曲线为阿基米德螺旋线的双驴头抽油机设计中，其模型中会出现极其复杂的超越方程，在其优化设计和分析中的一、二阶微分计算带来了极大的不便，以前常采用计算程序来完成一、二阶微分计算，这需要大量的、繁复的编程工作。文中提出了一种数值分析方法，即结合MATLAB中提供的差分函数，编制简单的M文件，就可以方便地完成双驴头抽油机后驴头型面设计的运动学分析和动力学分析中的一、二阶微分计算。

1 运动学分析模型

双驴头抽油机的机构原理如图1，其中，曲柄连杆机构是OTBO1，其连杆BT和摇杆OT的长度是随着曲柄O1B的转角θ的变化而变化。设计要求是：工作时，当悬点载荷较大时，游梁后臂C的有效长度变大，这使得曲柄转矩不致过大；当悬点载荷较小时，游梁后臂有效长度变小，使曲柄转矩不致过小，从而降低净转矩值，并使转矩因数按正弦规律变化，以得到精确的平衡效果。

图1中的后驴头型面O2T为阿基米德螺线，游梁支点设置为坐标系原点O，O1为曲柄旋转中心，O2为后驴头型面曲线极点，OO2为极心距，O2A为阿基米德螺线O2T的极轴。已知条件为：O2A与OO2的夹角为ε，γo为游梁最大摆角的1／2。假设R为曲柄半径、I为机架OO1水平投影、H为其垂直投影、C为游梁后臂长度、b为极心距OO2的长度、e为阿基米德螺旋线常数、L为游梁前臂长度、Lmin为最小连杆长度、θo为上冲程初始角、λ为极位夹角。上述变量长度量纲为米（m），角度量纲为弧度（rad）。

图1 双驴头抽油机的机构原理

为了进行运动学和动力学分析，首先在几个特殊位置进行一些基本参数的计算。

1） 当曲柄转角θ＝θo处于下死点位置时。

参见图1，游梁后臂长处于最大值，有如下关系成立

由式（1）～（2）可解得ξb，ξb为此时阿基米德螺线与连杆BT切点处的极角。利用MATLAB中的fzero函数可以求解ξb。

同时可求得在此位置最小连杆长度Lmin

2） 当曲柄转角θ处于任意位置时。

有如下关系存在：

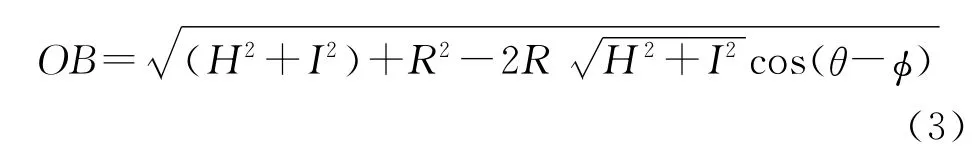
同时有

由式（3）～（4）可解得该位置时的ξ。ξ为此时阿基米德螺线与连杆BT切点处的极角。

3） 任意瞬时游梁摆角γ。

在求得以上一些参数后，则游梁的任意瞬时摆角γ可按以下模型求得，由图中的各角度关系

2 运动学的数值分析

由式（5）可见，若求得游梁的任意瞬时摆角γ，必须先完成式（1）～（4）的求解；若求得游梁悬点的速度和加速度，必须完成式（5）的一次和二次微分，对这么复杂的超越方程求解析微分几乎是不可能的。但在MATLAB中，利用diff函数的差分计算近似地代替微分计算，只要差分点取得足够密，工程计算的精度是可以保证的。这样就无需进行式（5）一次和二次微分。即在求得不同的曲柄转角θ的对应的游梁摆角γ后，则，游梁悬点的速度和角速度为

式中ω是曲柄的角速度。可见在求得了数组［θ］和［γ］后，差分计算是容易完成的。

以某厂生产的10型双驴头抽油机结构尺寸为例：R＝1 180 mm、S＝5 000 mm、L＝3 935 mm、I＝2 300 mm、H＝4 950 mm、b＝250 mm、e＝770 mm、ε＝135°。其中变量S为冲程，其余变量同前。按上述方法得到悬点加速度曲线如图2所示。

图2 悬点加速度曲线

图中曲线是按不同的冲次计算得到的，抽油机冲次越高，悬点的加速度越大。修改上述基本参数，可以得到不同机型或不同冲程的悬点运动情况，在此不赘述。

3 动力学的数值分析

完成了运动分析后，在任意时刻，双驴头抽油机的转矩因数可由式（8）求得

式中的各不同参量求解是在运动分析中完成的，则式（8）也是可求的。图3是按不同的冲次求得的转矩因数曲线，冲次越高，转矩因数越大。同理，也可以按不同的机型，或不同冲程分析转矩因数TF。

图3 双驴头抽油机转矩因数TF曲线

4 结论

1） 后驴头型面是阿基米德螺旋线的双驴头抽油机的性能要优于其他2种（渐开线和圆弧），但其型面设计模型中含有大量的超越方程，这给运动分析和动力分析的微分运算带来了极大的困难。

2） 本文中利用 MATLAB的fzer o函数和diff函数，编制相应程序，提出的一种数值分析方法，可以方便地解决这个问题。以某型双驴头抽油机的结构尺寸为例，给出了其悬点加速度和转矩因数曲线的计算过程，计算精度满足工程设计的要求。

3） 该方法可以应用于双驴头抽油机优化设计，以及双驴头抽油机使用过程的故障分析。但是，该方法若应用于双驴头抽油机程序化设计模块中，必须解决有关应用软件的相容性和接口设计问题。

［1］ 杨冬平，高学仕，戴扬.双驴头抽油机变参数柔性连杆机构动态仿真系统［J］.机械工程学报，2010（5）：59-64.

［2］ 戴杨，陆玲，高学仕.双驴头抽油机的运动与动力特性分析［J］.机械设计，2004（1）：26-28.

［3］ 连颍.双驴头抽油机的动力学分析与优化设计［D］.南京：南京理工大学，2007：15-23.

［4］ 王常斌，朱云伟.双驴头抽油机运动特性［J］.大庆石油学院学报，2011（2）：86-90.

［5］ 闫金涛.不同后驴头弧线形式的双驴头抽油机动力学仿真研究［D］.大庆：东北石油大学，2012：43-46.

［6］ 宋振华.复合平衡式双驴头抽油机动力学仿真分析［D］.大庆：东北石油大学，2012：19-28.

［7］ 刘华博，刘娇霞，孙鹤，等.双驴头抽油机运动动力特性对比分析［C］／／北京力学学会第19届学术年会论文集.2013：577-579.

［8］ 刘健，綦耀光，肖世宏，等.阿基米德螺线双驴头抽油机优化设计［J］.石油矿场机械，2001，30（3）：14-17.

［9］ 綦耀光，刘健，肖世宏，等.后驴头为圆弧的双驴头抽油机运动和动力分析［J］.石油矿场机械，2001，30（3）：4-8.

［10］ 邹龙庆，宋振华.双驴头抽油机优化设计与运动学仿真分析［J］.石油矿场机械，2012，41（6）：21-25.

Numerical Analysis Method for Outline Shape Design of Rear Horse Head of Dual Horse Head Pumping Unit

XU Feng-ping，ZHAO Zhi-cong，ZHOU Yan
（College of Mechanical Science and Engineering，Northeast Petroleum University，Dqaqing 163318，China）

The outline shape of rear horse head has enor mous influencing on the perfor mances of dual horse head pu mping unite，so t he opti mal design may be made to obtain t he outline shape of rear horse head.In this way accurate balance to dual horse head pu mping unite can be obtained to achieve saving ener gy and reducing consu mption.Because t here was co mplex transcendental equation in the model which opti mal design would be made in dual horse head pu mping unite which t he rear horse head outline shape was Archi medes spiral，so t he analytical sol ution was difficult to obtain.In this paper，combining with MATLAB f unction to program M-file a nu merical analysis met hod was given so t hat t he first and second diff erential coefficient coul d be calculated easily，thus kinematic and dynamic analysis of pu mping unite could down easily and so did opti mal design.The nu merical anal ysis met hod was si mple and easy，by taking difference instead of differential the basis of numerical analysis method was given for perfor mance analysis of dual horse head pumping unit，and computing precision was enough to meet the requirement of engineering design.

dual horse head pu mping unit；Archi medes spiral；nu merical analysis

TE933.101

A

1001-3482（2014）06-0021-04

2013-12-20

国家科技支撑计划“石油装备制造业创新技术服务平台建设”（2012BAH28F03）

许冯平（1964-），男，江苏海安人，教授，硕士，1988年毕业于东北石油大学，现从事特种机器人、机器人机构学和石油机械研究设计工作，E-mail：xufengping640724＠sohu.co m。