基于FPGA的STA-CORDIC算法在SCME中的应用*
王华华,陈雷成,陈发堂,李 明,汪朋锐
(重庆邮电大学 重庆市移动通信技术重点实验室,重庆 400065)
无论 SCM (Spatial Channel Modeling)、SCME 还是WINNERII等信道建模过程中,在信道矩阵欧拉公式展开后都有嵌套三角函数的实时参与。常用的计算三角函数方法有查找表和CORDIC算法[1],考虑到造价成本,FPGA资源并非无限大,而计算结果精度与存储空间相互矛盾,于是随着需求精度的增加查找表容量成指数增长从而优势渐无,而CORDIC算法则以空间换时间,只是进行加减和移位运算[2],所以其在FPGA实现中较为方便。
关于CORDIC算法的硬件实现方案,HU YH等人提出的角度编码CORDIC算法可以大幅度减少迭代次数[3],但提高了算法迭代时间和面积消耗;WANG S等人提出了一种更好的角度选择函数[4-5],但是与AR CORDIC算法相比其迭代次数要多很多;参考文献[6]提出的分解旋转角度的方法与传统CORDIC算法比较所需时钟周期要大得多。针对上述现状,本文提出了STA-CORDIC算法,即在传统CORDIC算法仿真结构之外增加算法精度与迭代次数、定点比特数之间多参量误差统计分析模块,之后基于Xilinx公司Virtex-6芯片做算法FPGA实现。
1 SCME过程中CORDIC算法的应用
经过路径损耗、阴影衰落、收发两端天线增益、MS端移动速度和方向、天线阵列到达角和离开角处理等相关操作之后,得到了U×S的(U和S分别为收发端天线数)信道传输矩阵 Hn(t),其中第(u,s)个元素如下[7-8]:
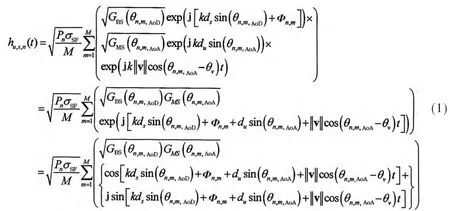
从式(1)中可以看出在θn,m,AoD和θn,m,AoA正弦值的处理过程中以及自然指数的欧拉展开式中,嵌套三角函数的实时处理极为关键。
2 CORDIC算法的性能分析
根据式(2)分别求得最大误差Emax、平均误差 E和均方根误差E,以便分析计算仿真后数据与真实数据之间的误差。
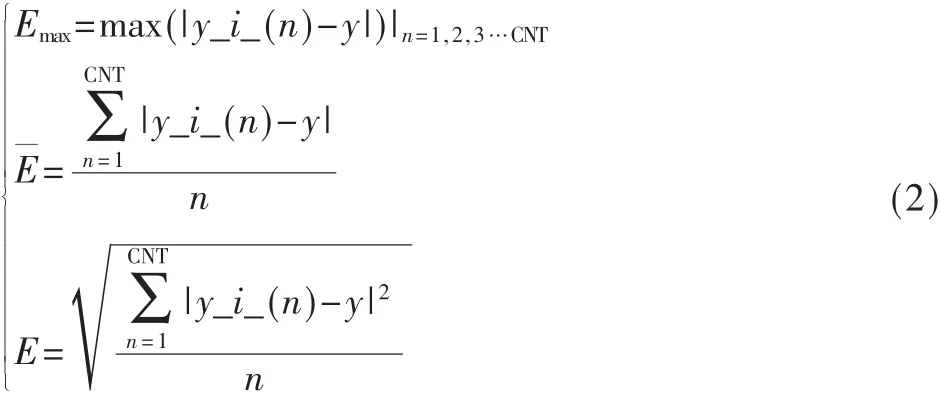
虽然理论上迭代次数越大、定点比特数越多仿真效果会越好,但是由于实际环境下软硬件资源的限制、运行延时时间以及成本等方面的考虑,在应用CORDIC算法计算正余弦函数时,在满足研究具体要求的前提下,迭代次数和定点比特数应该尽可能小。
2.1 迭代次数对仿真结果精度的影响
设定定点比特数为BYTE=32 bit,当迭代次数CNT低于5时,计算结果精度太低不予考虑。本文选择CNT=[5,6,7,8,9,10,11,12,13],根据式(2)在[0,2π]内分析不同迭代次数对仿真结果的影响,如图1所示。从图1知道,随着CNT的增大,各误差参量急剧降低。在CNT=10以后,各误差参量变化差别较小,即在精度要求不太高时,10次迭代足以满足一般情况下研究对算法精度的要求。
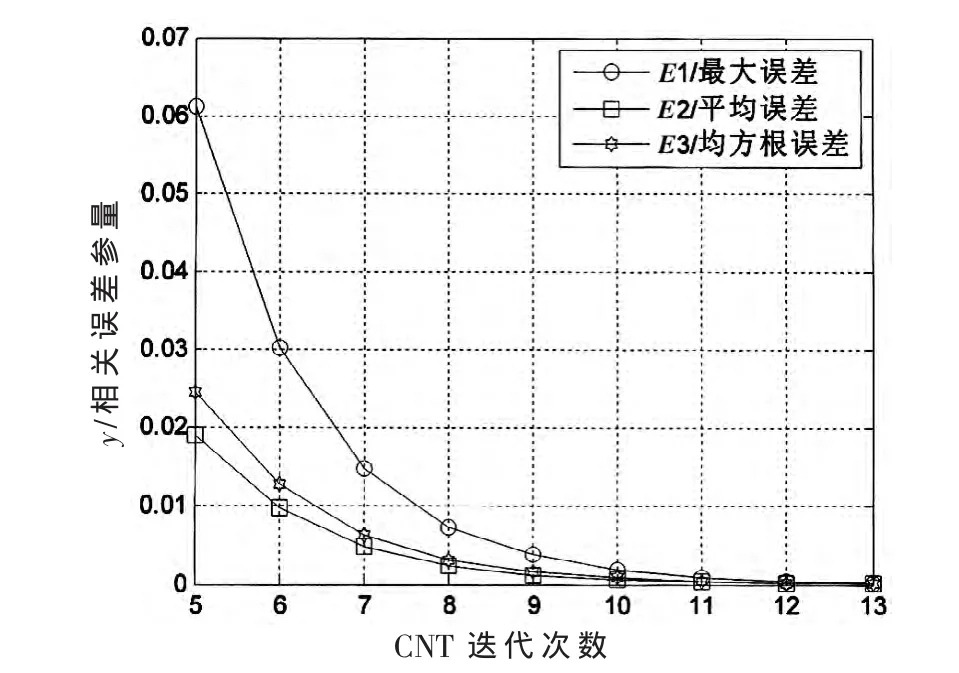
图1 各误差参量随CNT变化情况
2.2 定点比特数对仿真结果精度的影响
固定迭代次数CNT=13,一般情况下,定点比特精确位数不会超过32 bit,所以此时取BYTE=[10,32]区间中的数值,同样根据式(2)分析不同定点比特数对仿真结果精度的影响,如图2所示。
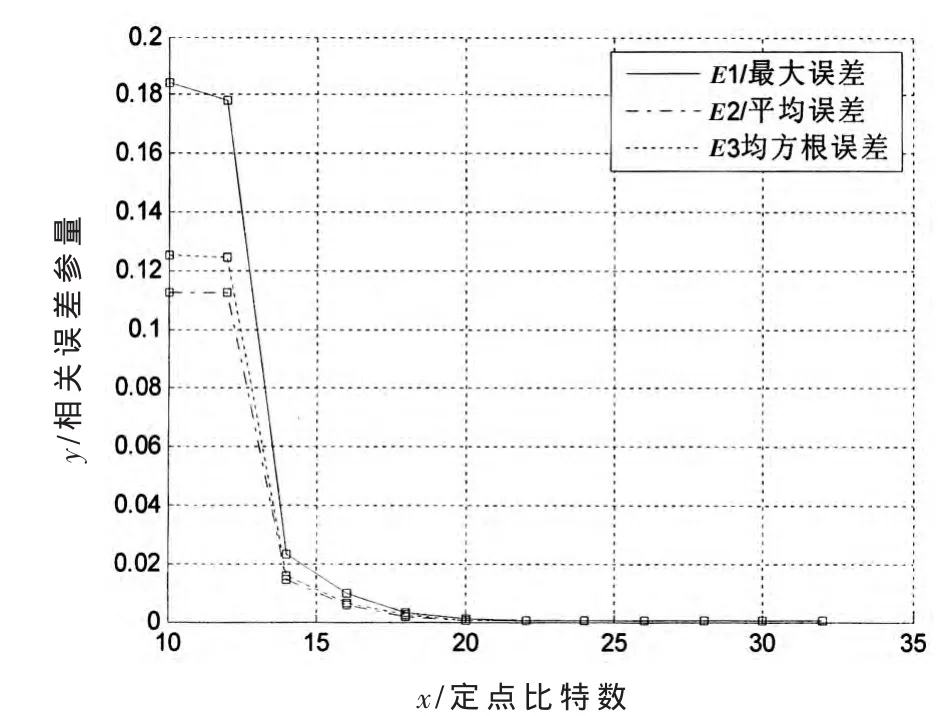
图2 各误差参量随BYTE变化情况
从图2中看到,随着BYTE的增大,各误差参量骤然降低。尤其在BYTE=20以后,各误差参量变化差别较小,数值已在很小的数量级上。即在精确度不甚高的时候,只取BYTE=20就能够满足研究需求。
3 固定弧度值处CNT和BYTE对算法精度的联合影响
为了研究采取不同CNT和BYTE时,计算结果精度随之变化情况,固定角度为π/4进行仿真研究。角度为π/4时,仿真函数值和真实函数值的图像如图3所示,图4为此时仿真值与真实值之间的误差绝对值图像。
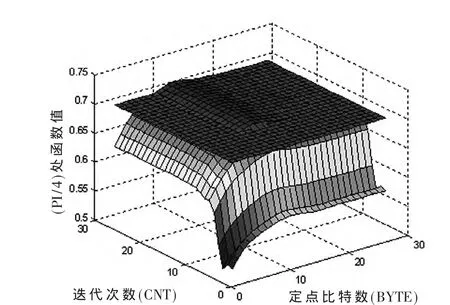
图3 角度π/4时仿真和真实函数值图像
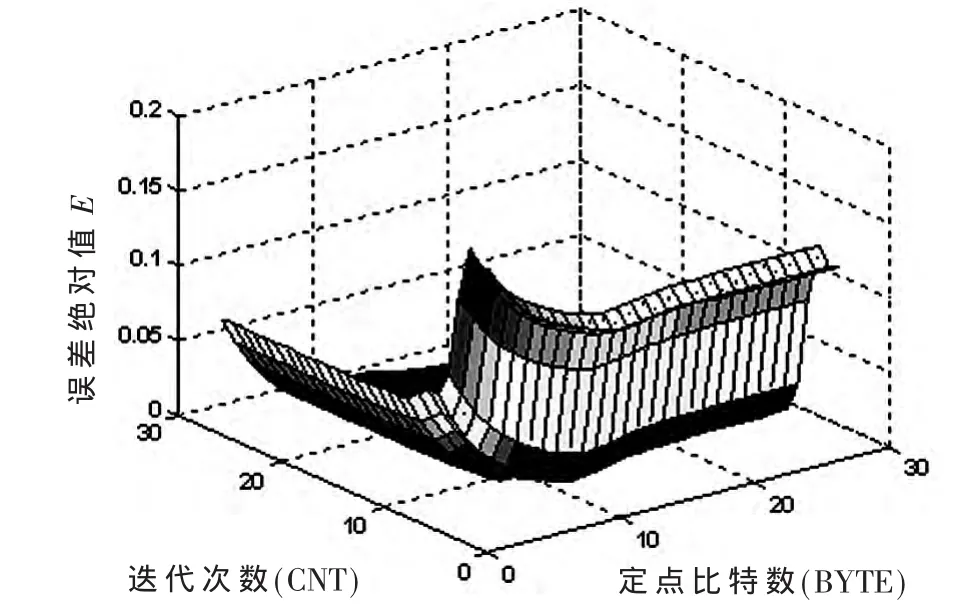
图4 角度π/4时仿真函数值误差绝对值
图3显示采取不同的CNT和BYTE时,一定范围内迭代次数比定点比特数对结果精度影响大。图4显示在CNT小于10时,误差绝对值迅速增高,即计算结果精度迅速降低,而一定范围内精度误差绝对值随BYTE变化较缓慢。
4 算法FPGA设计及仿真分析
4.1 算法设计流程
STA-CORDIC在传统算法结构之外,添加了一个统计分析模块。通过特定角度及其正余弦函数值对所建模型进行需求精度循环优化,在满足精度要求后,确立好最优模型,之后计算目标角度的函数值。具体结构如图5所示。
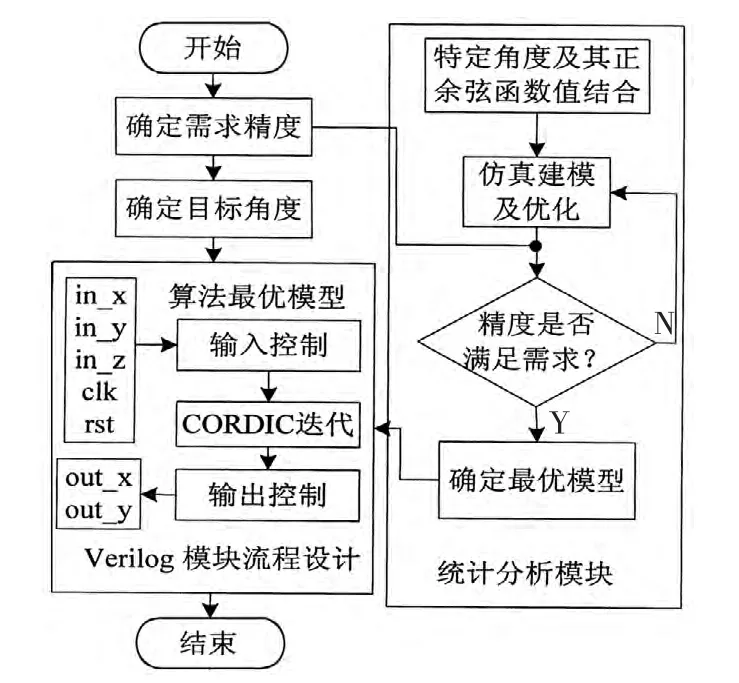
图5 STA-CORDIC算法结构
CORDIC算法的实质即为硬件移位与加减操作,首先确定需求精度进而得出收缩因子K值,之后输入待求角度,通过基础角度集合中角度的积累,逐渐逼近目标角度,剩余角度渐趋为零。CORDIC算法硬件实现流水线结构如图6所示。
4.2 算法的仿真分析
基于以上分析,选取BYTE=32、CNT=13和 BYTE=20、CNT=10两种情况下做硬件仿真实现。算法ModelSim仿真图如图7和图8所示。
对比图7和图8,可以看出两者之间的误差值在允许范围之内。但图7条件下(情形2)所用资源能比图8(情形1)所用资源节省许多,两者对比如表1所示。
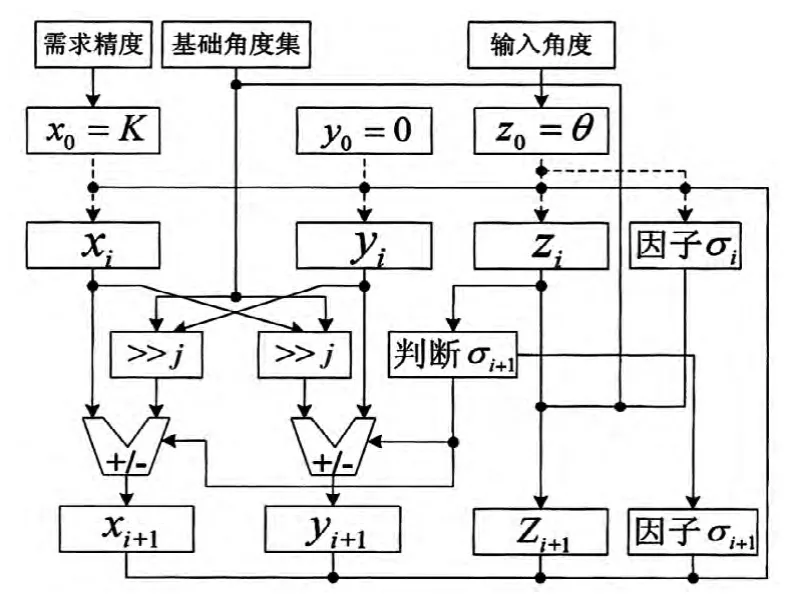
图6 CORDIC算法的PIPELINED结构

图7 BYTE=32,CNT=13条件下仿真图像
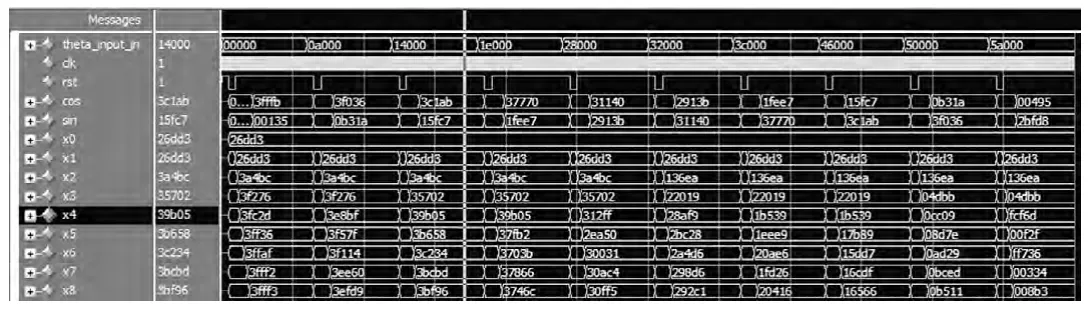
图8 BYTE=20,CNT=10条件下仿真图像

表1 两种情形下算法结果精度与资源消耗对比
从表1中可以看出,情形2比情形1精度稍有欠缺,但尚在误差允许范围内。另一方面,在逻辑资源、寄存器、存储资源消耗和延时对比中,情形2有较大的优势。即此时用较小的精度差值换得了资源上的节省。
本文在理论可行性分析基础上,提出了在传统CORDIC算法增加了优化模块的STA-CORDIC算法,在MATLAB仿真之后基于Xilinx公司Virtex-6芯片做了算法FPGA实现,通过资源消耗和延时等因素对比得出了STA-CORDIC算法操作的优势性。
[1]VOLDER J E.The CORDIC trigonometric computing technique[J].IRE Transactions on Electronic Computers,1959,EC-8(3):330-334.
[2]MEHER P K,VALLS J,JUANG T B,et al.50 Years of CORDIC:algorithms,architectures and applications[J].IEEE Transactions on Circuits and Systems—I:Regular Papers,2009,56(9):1893-1907.
[3]HU Y H,NAGANATHAN S.An angle recoding method for CORDIC algorithm implementation[J].IEEE Transactions on Computers,1993,42(1):99-102.
[4]WANG S,PIURI V,SWARTZLANDER E E.Hybrid CORDIC algorithms[J].IEEE Transactions on Computers,1997,46(11):1202-1207.
[5]张德民,朱翔,李小文.LTE系统中小区搜索定时同步的FPGA设计[J].电子技术应用,2013,39(9):24-27.
[6]WU C S,WU A Y,LIN C H.A high-performance/lowlatency vector rotational CORDIC architecture based on extended elementary angle set and trellis-based searching schemes[J].IEEE Transactions on Circuits System II:Analog Digital Signal Processing,2003,50(9):589-601.
[7]3GPP,Multiple Input Multiple Output(MIMO)simulations(Release9).(3GPP TS25.996),v9.0.0.[EB/OL].[2014-02-18].http://www.3gPP.org.
[8]BAUM D S,ZURICH E,SWITZERLAND,et al.Aninterim channel model for beyond-3G systems:extending the 3GPP spatial channel model(SCM)[J].Vehicular Technology Conference,2005(5)3:132-3136.

