提高雷达速度分辨率的线性调频Z变换方法*

孔 伟，曾 荣，王 成，张智源

(中国华阴兵器试验中心，陕西华阴 714200)

0 引言

弹箭飞行速度影响武器系统的射程、射击精度和寿命等性能［1］，在常规靶场武器弹药的定型、鉴定、射表编拟及科研摸底等试验中，常常需要对目标飞行速度进行测量。

基于FFT分析技术的连续波测速雷达具有测速精度高、设备简单、机动性强等优点，在各国靶场得到广泛应用。FFT分析技术等效于用一组数字滤波器对输入信号进行滤波，当雷达波束内的多个目标之间的速度差大于雷达速度分辨率时，雷达可以对多个目标进行检测。

FFT对多普勒频移的物理分辨率［2］取决于所分析的信号长度，测量信号长度一定，选择补零计算及不同的窗函数计算仅仅对速度频谱进行了某种改善，不能提高速度分辨率，影响多目标的测量精度。

实际测量中，目标飞行时间是一定的，这就决定了FFT的速度分辨率，限制了多目标检测能力。针对FFT对于雷达速度分辨率存在的局限性，文中提出了线性调频Z变换方法。

1 频域速度测量

速度分辨率是指雷达区分两个具有不同多普勒频移的目标的能力，当速度分辨率大于目标之间的速度差时，这些目标将被视为一个目标，不能有效分离;当速度分辨率小于目标之间的速度差时，多个目标可得到有效分离。

目标速度与多普勒频移存在下述关系［3］:

式中:vr为目标与雷达天线连线方向上的速度(m/s)，是目标飞行速度在天线径向上的一个分量;c为光速(m/s);fd为多普勒频移(Hz);f0为雷达发射机工作频率(Hz)。

由式(1)知，雷达速度分辨率实质是对多普勒频移的分辨率，提高雷达速度分辨率本质是提高多普勒频移的分辨率。

对雷达接收机信号按下式进行FFT计算［4］:

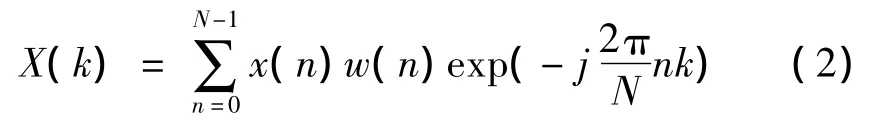
式中:X(k)为FFT计算结果;x(n)为雷达接收机信号;w(n)为窗函数，用于选取计算点数及抑制频谱泄漏。

信号在频率 fk=kfs/N，k=0，1，…，N－1处的功率为:

N点FFT计算等效信号通过N个中心频率

为fk的数字滤波器组后的输出，当多普勒频移落在第m个滤波器通带内时，对应的P(m)在瀑布图上表现为一个峰值，对瀑布图进行速度搜索得到目标的飞行速度时间曲线。

FFT计算频谱能够得到的频率最大分辨率［2］为:

式中:Δf为频率分辨率(Hz);fs为采样频率(Hz);N为采样信号点数;Ts为采样间隔(s);T为信号长度(s)。

由式(4)知，FFT最大频率分辨率取决于信号长度，当测量信号的长度一定，FFT对速度的分辨率也就确定了，补零计算及改变窗函数都没有增加信号的实际测量长度，仅仅是对频谱作了某种“视觉”改善，不能提高真实的速度分辨率。

2 单位圆上的线性调频Z变换［2，5］(CZT)

信号x(n)的线性调频Z变换为:

式中:

图1 CZT的变换路径

幅角θ0是线性调频Z变换计算起点，φ0是计算步长，A0、W0为任意的正实数，取 r=0，1，2，…，M－1的 Z 变换，得到如图1 所示的由 z0，z1，z2，…，zM－1连接的一条螺旋线。

为分析信号的频谱，应在单位圆上实现CZT，此时，A0=W0=1，信号长度取N点，变换长度取M点，由于:

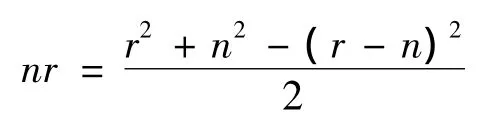
式(5)可写成:

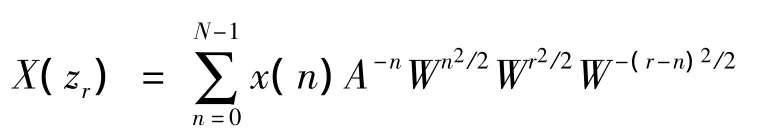
令:

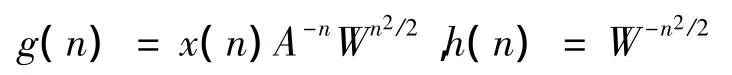
则:

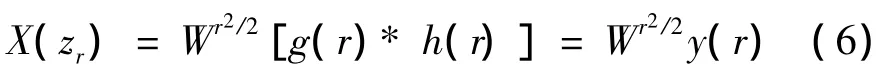
式中:

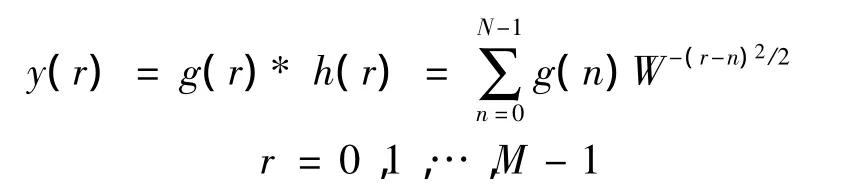
综合上述计算过程，CZT的线性滤波计算可用图2所示步骤实现。

图2 CZT的线性滤波计算步骤

由图2可见，计算单位圆上M点X(zr)的关键是实现g(n)与h(n)的线性卷积，这可以通过FFT来实现。

单位圆上的CZT转化为FFT，可以进行信号的频谱分析，在单位圆上θ0是待分析信号的起始频率，φ0是频率计算步长，理论上这两个参数可任意给定。

因此，在实际测量中可以根据对测量信号频率分辨的要求，选择适当的起始频率θ0及步长φ0进行CZT计算，对感兴趣的一段频谱进行“细化”，以提取有用信号。

3 仿真实验

在MATLAB环境下［6］进行3个飞行目标测量仿真实验，实验信号取自连续波测速雷达接收机输出的零中频信号，对信号采样后分别进行FFT分析及CZT分析，具体过程如下。

3.1 生成实验信号

实验条件:雷达发射频率10.500 GHz，雷达波束中存在3个飞行目标，接收机输出的零中频信号由3个正弦信号 f1=20 kHz、f2=20.04 kHz、f3=20.5 kHz及高斯白噪声组成，多普勒频移对应的目标速度小于300 m/s，采样频率 fs=62.5 kHz，信号长度取 1 024点(16.384 ms)，信噪比SNR=12 dB，实验信号为:x(t)=sin(2πf1t)+sin(2πf2t)+sin(2πf3t)+n(t)式中:x(t)为对应3个目标、由3个正弦信号及高斯白噪声叠加的实验信号;n(t)为均值为零、方差为0.284(对应信噪比SNR=12 dB)服从高斯分布的白噪声。

图3是生成的仿真实验信号。

图3 仿真实验信号

3.2 FFT分析计算

根据式(2)、式(3)对实验信号进行FFT计算，其中窗函数取哈明窗，计算结果如图4所示。

图4 仿真实验信号哈明窗FFT计算结果

从图中峰值标记点可以看出，FFT计算分辨出含有频率f2与f3两个信号，但不能识别含有f1频率成分的信号。

改变FFT计算的窗函数，将哈明窗换为主瓣最窄的矩形窗，重新计算式(2)、式(3)，结果如图5所示。

图5 仿真实验信号矩形窗FFT计算结果

由图5结果知，尽管矩形窗函数的主瓣宽度是哈明窗的一半，但也没有将3个信号成分有效分离，仅仅是放大了峰值。

选取哈明窗或矩形窗，其主瓣对信号进行了“平滑”，边瓣对信号产生了泄露，二者都没有分辨出3个信号成分，仅仅是对速度频谱进行了某种改善。

事实上，对于分析的仿真实验信号，fs=62.5 kHz，M=1 024，由式(4)知:

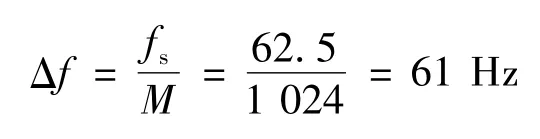
FFT计算频谱能够分辨的最大频率为61 Hz，显然，由于f2－f1=40 Hz＜Δf，所以不能分辨由f1产生的正弦分量;f3－f1=500 Hz＞Δf，所以能分辨由f3产生的正弦分量。

3.3 CZT 分析计算

CZT计算参数选择为:变换长度取710点，变换步长取10 Hz(小于40 Hz)，变换起点18 kHz，根据这些参数计算式(6)，得到如图6所示计算结果。

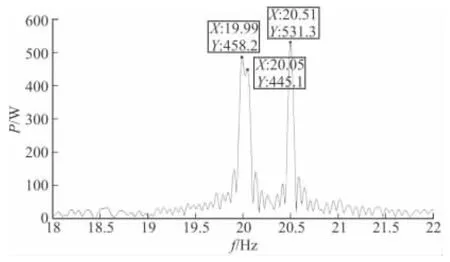
图6 仿真实验信号CZT计算结果

图6是在18～22 kHz这一段频率范围求出的傅里叶变换，分点较细，3根谱线都可分辨出来。

将FFT与CZT对实验信号的分析处理结果显示在图7所示的同一坐标系下。

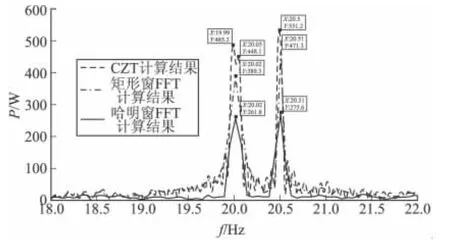
图7 仿真实验信号CZT与FFT计算结果

可以清晰看到，在不能增加信号长度条件下(本例信号长度固定1 024点、16.384 ms)，对于FFT计算不能分辨的频率分量，通过CZT计算能够有效分离，提高了频率分辨率，增强了多目标测量能力。

4 结论

实际测量中连续波测速雷达一次采样获得的信号长度是固定不能增加的，FFT计算频谱能够得到的频率最大分辨率也就确定了。此时，利用线性调频Z变换可以计算单位圆上任一段圆弧的FFT，计算时的输入点数和输出点数可以不相等，在不增加多普勒测量信号长度条件下能够对频谱“细化”，提高多普勒频移的分辨率，增强测速雷达多目标测量能力。

仿真实验表明，不增加分析信号的长度，在单位圆上计算CZT，选择适当的计算起点、计算步长及计算长度，可以进一步提高频率分辨率，突破FFT最大频率分辨率的限制。

将这一算法应用到测速雷达中，可以提高连发射击、子母弹开仓点等多目标的测量能力。

［1］李益民.弹道测量雷达及在兵器试验中的应用［M］.北京:国防工业出版社，2010.

［2］胡广书.数字信号处理理论、算法与实现［M］.3版.北京:清华大学出版社，2012.

［3］丁鹭飞，耿富录.雷达原理［M］.3版.西安:西安电子科技大学出版社，2003.

［4］万建伟，周良柱，皇甫堪，等.测速雷达中的谱分析技术［J］.弹道学报，1995，7(4):71-76.

［5］陈怀琛.数字信号处理教程－MATLAB释义与实现［M］.2版.北京:电子工业出版社，2008.

［6］张志涌.精通MATLAB 6.5版［M］.北京:北京航空航天大学出版社，2003.