基于ML的OFDM优化同步算法

陈 能，陈 颖，邓 强

(西南电子技术研究所，四川 成都 610036)

早在 20世纪 60年代，OFDM （Orthogonal Frequency Division Multiplexing）技术以其高频谱效率、抗多径干扰等优势,就已经被应用到多种高频军事通信系统中,其中包括美国的 ANDEFT、KINEPLEX以及 KNTHRYN等[1]。直到70年代，人们提出了采用IDFT/DFT来实现多载波的调制/解调，简化了系统结构，才使得OFDM更趋于实用化。

OFDM的主要问题是对同步误差非常敏感,尤其是定时误差和频偏误差，在载波数较多的情况下甚至微小的同步误差都可能引起严重的码间干扰和符号间干扰，造成信号幅值的衰减和相位旋转，从而极大地降低系统通信性能。

本文采用了多符号的ML算法,提出了2种定时估计方法和与之相应的3种频偏估计方法。从理论上讲，多符号的ML算法利用了多个传输符号和干扰项的统计特性，能优化算法中数据的相关性，减小判决误差。

1 同步误差对系统的影响

1.1 同步误差分析

OFDM系统的同步偏差主要包括：发射机与接收机晶振频率偏差造成的收发失配和移动通信中的多普勒频移的影响；接收端对发送的数据符号的到达时刻的不确定性；发送端D/A模块与接收端A/D模块的采样频率不完全一致而存在偏差。综合可得OFDM系统中的同步要求主要有3种：

载波同步：对应发送端调制模块，接收端解调模块，要求实现两模块载频一致；

符号同步：对应IDFT、DFT模块，要求接收端准确判断符号起始位置进行DFT运算；

采样同步：对应于系统中D/A、A/D转换模块，要求发送端数模变换与接收端模数变换的采样频率一致。

1.2 频率偏移误差对系统的影响

由OFDM原理可知其对频率偏移非常敏感，很小的频偏误差将导致接收端子载波间的正交性被破坏。

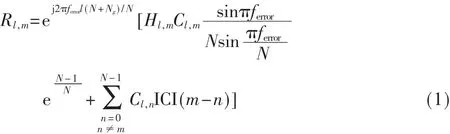
[2]中提出存在加性高斯白噪声和频率偏移量ferror的情况下,接收端的有效信噪比为式(2)所示。

由式(2)可知，如果系统中没有白噪声干扰，为了实现接收端有至少30 dB的信噪比，频偏值应满足|ferror|≤1.3×10-2，因此，对频偏的估计误差精度最小应保持在子信道频率间隔的1.3%。

1.3 符号同步误差对系统的影响

由于传输时延，接收机无法确定信号何时到达接收端，存在一个采样定时偏差Δτ。用采样间隔Ta归一化，可得定时偏差：

其中：s∈Z, τ0＜Ta。

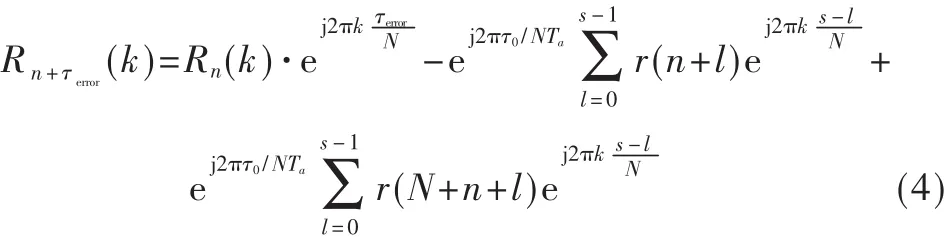
由式 (4)可以看出符号同步误差的影响有两个：(1)在准确的解调信号上产生了一个相位旋转因子，其大小与子载波位置k成正比，后果是在星座逆映射过程中产生误码；(2)当定时偏移量超过一个采样周期,即 s≥1时，就引入了ISI项。

1.4 采样同步误差对系统影响

设收发两端采样时钟偏差为ΔT，因此可将对第n个OFDM符号的第k个子载波的采样时刻表示为：tn,m=[(N+Lg)·n+k](Ta+ΔT)，则：

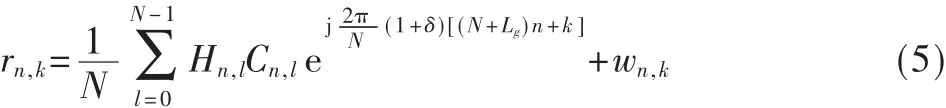
由式 (5)可知采样时钟偏差带来的问题主要有两个：(1)符号定时漂移，从而造成了子载波的相位旋转；(2)采样频率偏差造成了子载波间的正交性被破坏，引入了ICI，从而引起接收端SNR损失。

2 经典同步算法概述

SCHMIDL T和COXT D算法[3]找到的定时测度M(d)最大的点即是接收数据符号起始时刻。但是仿真发现，这种方式实现的定时测度函数并非一个尖锐峰值，而会出现一个峰值平台，从而造成了定时模糊。

MINN H算法[4]获得的定时同步是在SCHMIDL T和COXT D算法的基础上进行的改进,将其模糊平台转化成尖峰值，但由于其本身的帧结构,其测度函数出现了不止一个峰值，混淆判决。

Moose算法[5]中，发射机对一个OFDM符号重复发射。该算法是在频域进行处理的，主要用于频偏估计，因此需要额外的FFT模块，增加了接收端的复杂性。

部分窗相关算法[6]主要用于消除多径的影响，它利用CP中无多径干扰的部分来做定时频偏估计，在已知多径最大时延的条件下可实现很好的估计，但在现实中是以牺牲传输的效率来换取定时的准确性。

最大相关算法[7]是ML算法的简化算法，只考虑了CP与数据部分的相关性，因此其计算复杂度较ML算法大大降低。但是当信噪比较大时能量项不能忽略，此时定时估计误差较大。

ML算法[8]对于定时和频偏的估计是以假设信道为加性高斯白噪声为前提的。当存在多径干扰时，CP部分与数据的相关性受到影响，此时估计抖动较大，错误率高达95%。无线通信中的信号基本都是多径的而且干扰严重，如何有效抗干扰是包括ML算法在内的各种同步算法需要解决的问题。

3 ML原理及算法改进

3.1 ML算法原理

最大似然联合实现符号定时同步和载波同步法，是基于循环前缀与数据部分的相关性，既可以实现定时估计，也可以相对准确地进行频偏估计,数据帧结构如图1所示。

图1 ML算法数据帧结构

假设符号定时偏差和频率偏移分别为θ和ε。使用ML方法对两种偏移进行联合估计的方程为：

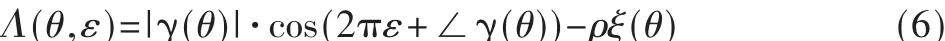
由下面公式得到定时估计值和频率偏差值：

3.2 改进的ML算法

本文将在ML算法原理的基础上进行数据帧结构和判决方法的改进。在ML算法中，是基于2N+L个样值来考虑的，换言之，根据这样的模型得到的估计器仅仅用到了当前OFDM符号的信息来对每个符号的定时偏差和频率偏差进行最大似然估计，这种方法易受干扰影响，判决误差比较大。可以利用多个OFDM符号联合估计，来改善估计器的性能，数据帧结构如图2所示。

图2 基于多符号的ML算法数据帧结构

每进行一次ML算法判决需要连续3个数据符号中的(2N+L)个样值，但进行M次ML运算只需要 M+1个数据符号，其中部分数据符号复用，即利用M(N+L)+N个样值进行同步估计。

定时估计方法1将M个数据符号运用公式(9)计算Λ(θ,ε),即根据连续 M+1个数据符号具有相同的定时偏差和频率偏移,将M次ML运算进行累加，根据ML定时判断准则估计相应的θ^的值。

定时估计方法 2，每次 ML运算的(2N+L)数据(除高斯白噪声影响外)集合完全相同，即单个数据符号连续重复发送M+1次，运用公式(10)，即将 M次 ML估计用到的数据符号累加，减弱随机噪声干扰的影响，再根据ML 准则判断的值。

两种改进定时估计方法对应的Λ(θ,ε)值与 θ的关系如图3所示。

由图3可知，方法2的峰值最明显但旁瓣相对也大，方法1峰值也很明显，旁瓣相对较小，ML算法峰值附近波动较大，峰值不明显，相关性能最差。

与以上定时估计相对应本文提出了三种频偏估计方法。

图3 两种改进定时估计算法

频偏估计方法1利用M次ML估计的，根据公式：

再根据公式：

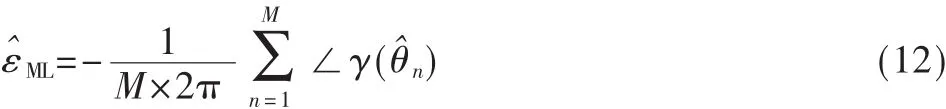
计算频偏。

频偏估计方法3与定时估计方法2相对应，由定时估计方法 2 得到的，利用公式(10)中的 r′(k)根据式(8)得 到 频 偏 估 计。

4 仿真分析

仿真参数：调制方式 QPSK，M=4，N=1 024，LCP=128，ε=0.25，θ=792。

仿真结果：定时估计仿真性能如图4所示，其中θi为第i种定时同步方法下定时均方误差。

由图4可知第一种方法性能最优，三种仿真结果性能由好到差顺序为：方法1＞方法2＞ML算法。

频偏估计仿真结果如图5所示，其中εi为第i种频偏估计方法下频偏均方误差。

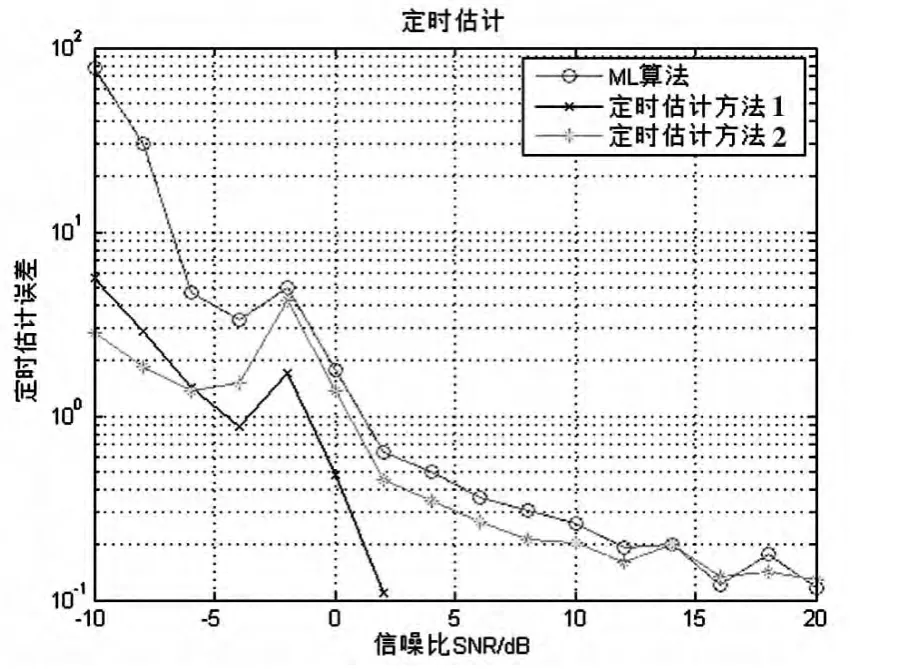
图4 两种改进定时估计算法性能

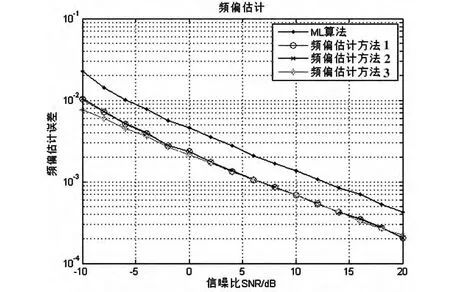
图5 三种改进频偏估计算法性能

本文提出的优化算法具有很好的抗干扰性能，特别适用于复杂恶劣的通信环境。定时估计方法2和频偏估计方法3均利用了M+1个相同数据符号，其仿真效果在低信噪比条件下比较好，且M越大性能越好，由图5和图6可知在定时估计性能提高有限的情况下频偏估计性能改善明显，但传输效率比较低，仅为ML传输效率的1/(M+1)。3种频偏估计方法性能比较接近，信噪比在-8 dB左右时3种频偏估计的误差均在1%以内，判决精度高。定时估计方法1在信噪比达到2 dB左右时定时估计准确率几乎为100%。这几种改进方法能实现较好的同步估计，但相比较ML算法需要更多的存储空间，且计算复杂度有所增加。同时本文中频偏估计方法的估计范围与ML算法的频偏估计范围一样,均为|ε|≤0.5，需要在小数频偏补偿后结合导频进行移位相关运算获取整数频偏[9]。

参考文献

[1]李引凡.OFDM技术及其关键技术[J].现代电子技术，2005，28(7)：25-30.

[2]MOOSE P H.A technique for orthogonal frequency division multiplexing frequency offset correction[J].IEEE Transactions on Communications,1994,42(10):2908-2914.

[3]裴明信.OFDM的同步技术研究和仿真[D].哈尔滨：哈尔滨工业大学，2012.

[4]梁小朋，邓茜，周勇锋.基于训练序列的定时同步算法研究[J].江西理工大学学报，2011，32(5)：46-48.

[5]MOOSE P H.A technique for frequency division multiplexing frequency offset correction[J].IEEE Transactions Commun,1994,43(10):2908-2914.

[6]TAKAHASHI K,SABA T.A novel symbol synchronization algorithm with reduced influence of ISI for OFDM systems[J].IEEE Global Transactions Commun,2001(01):524-528.

[7]STEFAN H,WEINFUTNER M.On the optimality of metrics for coarse frame synchronization in OFDM:A Comparison[C].9th IEEE PIMCR′98,1998:533-537.

[8]李艳苹，张礼勇.一种改进的OFDM定时同步算法[J].哈尔滨理工大学学报，2012，17(3)：62-64.

[9]许家富.OFDM同步技术及其在DVB-T中的应用研究[D].太原：太原理工大学，2008.