如何解决工农业生产销售中的优化问题

张少林

(丽江师范高等专科学校数学与计算机科学系,云南丽江 674100)

如何解决工农业生产销售中的优化问题

张少林

(丽江师范高等专科学校数学与计算机科学系,云南丽江 674100)

不论在工农业生产、经济学中,还是管理学、工程技术及科学实验中,小至日常用具的制作,大至生产科研和各类经营活动,都要讲究效率,考虑怎样以以最小的投入最大化的解决问题。这类问题统称为优化问题,也是每年考研数学必考内容,然而不少大学生在面临该类问题时,仍习惯于利用中学时代配方法求解,费时不少,吃力不小,却效果不好。本文仅举例说明在工农业生产销售中如何解决优化问题,希望对大学生的学习和备考有所帮助。

优化问题 函数的极值

不论在工农业生产、经济学中,还是管理学、工程技术及科学实验中,人们做任何事情,小至日常用具的制作,大至生产科研和各类经营活动,都要讲究效率,考虑怎样以最小的投入得到最大的产出,或者最大化的解决问题。这类问题,在数学上往往可以归结为求某一函数在某个集合内的的最大值或最小值问题,这个函数称为目标函数,函数取值的集合称为约束集或可行域。这类问题统称为优化问题[1]。该类问题也是每年考研数学必考内容,然而不少高校理工类、经济类、管理类等门类学生在面临该类问题时,仍然习惯于采用中学时代配方法求解,费时不少,吃力不小,却效果不好。本文仅举例说明在工农业生产销售中如何解决优化问题,希望对大学生的学习和备考有所帮助。

1 工农业生产销售中的优化问题实例

例1 从一块半径为R的圆铁片上挖去一个扇形做成一个漏斗。问留下的扇形的中心角φ取多大时,做成的漏斗的容积最大[1]？

解：设漏斗为一个半径为r,高为h的正圆锥,则中心角为φ的扇形铁片的圆弧之长Rφ就是漏斗的底圆之周长 2πr,即2πr=Rφ,而漏斗的高为于是漏斗的容积为

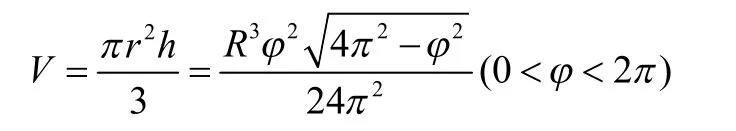
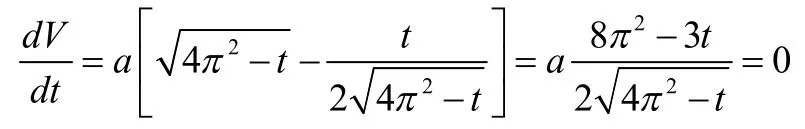
例2在在化工生产中,反应罐内的液态化工原料排出后会在罐壁上留下10kg的残液。现用一定的清水分两次冲洗反应罐,问如何分配两次的水量,才能使得第二次冲洗后罐壁上所留残液中化工原料最少[2]

解：设一定量的水为W,第一次用水量为x,则第二次用水量为W-x(单位kg)。冲洗前,化工原料残液为10,第一次冲洗放水后,残液中化工原料含量为,

第二次冲洗放水后,残液中化工原料含量为

两次冲洗效果最好就是R(x)最小,为此求f(x)=(10 +x)((10+W-x)(0 ＜x＜W)的最大值。

令f′(x) =W- 2x=0,得因f′′(x)=-2 ＜0, 故为最大,即

例3设某商品的需求量Q是单价P(单位：元)的函数Q=12000- 80P;商品的总成本C是需求量Q的函数C=25000 + 50Q;每单位商品需要纳税2元,试求使销售利润最大的商品单价和最大利润额[3]。

解：因Q=12000 - 80P,C=25000 + 50Q=25000 +50(120000 - 80P)=625000 - 4000P,

故 总 利 润 函 数L=PQ-C- 2Q=(P- 2)Q-C=(P-2)()(12000 - 80P)- 62500 + 4000P=- 80P2+ 16160P-649000

由此可见当P=101(元)时获利最大,且最大利润maxL=L(101)=167080(元)。

例4设平均收益函数和总成本函数分别为AR=a-bQ,,其中常数

a＞ 0,b＞0待定。已知当边际收益MR=67,且需求价格弹性时,总利润最大。求总利润最大时的产量,并确定a,b的值[3]。

最大的产量Q及相应的a,b应满足L′(Q)=0,MR=67 及即

把第一组数据中的a,b代入得总利润函数+ 11Q- 50,虽然L′(3)=0,L′(3 )＜0,即L(3)确实是L(x)最大值,但L(3)＜0,不符合实际,故应舍去。

把第二组数据中的a,b代入得总利润函数也有,L′(11)=0,即L′(11)＜ 0,即是L(x)的最大值,故a=111,b=2,是所求常数的值,使利润最大的产量Q=11。

2 小结

优化问题广泛存在于各行各业及日常生活生产实践中,本文所选实例只是沧海一粟, 但由上述事例可以看出解决优化问题要根据不同问题的具体情况采用不同的数学方法,首先根据实际问题,找出变量并列出目标函数f(x)的表达式,虽然函数极大值、极小值与最大值、最小值一般不同,但如果问题所涉及的目标函数具有连续性和可导性,可行域又是一个区间,往往可以采用微分学的方法加以解决：(1)求出目标函数f(x)的全部驻点(即求出方程的全部实根)与不可导点算出比较上述值的大小,就得到最大值和最小值;(2)若f(x)在x0处存在二阶导数且f(x)′≠0,当f(x)′＜0时,函数f(x)在x0处取得极大值,当

0时,函数f(x)在x0处取得极小值,即可确定最大值和最小值(如例2),从而解决优化问题,但一定要注意所求最值必须有实际意义,否则不是真的最值(如例4)。

由例1、例3可知,在实际问题中,如果根据问题的性质可以判断目标函数f(x)在其定义区间I内部确实有最大值和最小值,而f(x)在I内可导且只有唯一的驻点x0,那么就可以断言f(x0)必定是f(x)的最大值或最小值。不需要另行判定[1]。

[1]同济大学应用数学系.微积分(上册)[M].高等教育出版社,2002.169,175,173.

[2]同济大学应用数学系.武汉科技学院数理系.微积分学习指导书[M].高等教育出版社,2002.124.

[3]刘西垣,李永乐,袁荫棠.2012年数学复习全书(考研数学三经济类)[M].国家行政学院出版社.2011.106,113.