共源共栅两级运放的三种补偿结构分析和比较

胡利志，乔 明

（电子科技大学电子薄膜与集成器件国家重点实验室，成都 610054）

1 引言

运算放大器是许多模拟系统和混合信号系统中的一个完整部分，不同设计要求和复杂程度的运放被用来实现电路中的各种功能。

两级运放因为可以同时满足实现高增益和大输出摆幅的要求，而不像单极运放必须在增益和输出摆幅之间进行折中。两级运放的设计思路是将增益和摆幅要求分别处理，即运用第一级放大器得到高增益，第二级放大器主要实现大输出摆幅，并进一步提升增益，从而实现高增益和大摆幅的设计[1~3]。因此，在通用运算放大器的设计中，利用两级放大器结构来设计放大器被广泛采用。两级运放因为第一级和第二级输出电阻都较大，且存在一定的寄生电容，因此这两个极点距离不够大而需要进行补偿才能稳定工作。目前的两级CMOS运算放大器常采用米勒电容补偿技术[1]。

文中分析了以套筒式共源共栅结构作差分输入级的两级运放的三种米勒补偿方法，即带消零电阻的直接米勒补偿和两种共源共栅米勒补偿方法，依次进行了电路结构、小信号等效电路传递函数的分析比较，最后用0.18 μm CMOS工艺分别对电路进行了仿真，仿真结果与电路分析的结论相符合。

2 电路结构分析

两极运放的米勒补偿电路整体框图如图1（a）所示，这种补偿方法是直接将米勒电容接在运放的两级之间，利用米勒效应，通过移动两个相邻极点位置，即极点分裂（pole splitting）[1]，来改善电路的频率特性，如图1（b）。

图1 两极运放的米勒补偿技术及极点分裂

如图2所示，文中的两级运放主体结构可以看成两个单级放大器，套筒式共源共栅差分输入级和共源增益输出级，辅助电路为偏置电路和频率补偿电路。差分输入级采用共源共栅结构输入对管，PMOS共源共栅电流镜作为负载；共源级采用PMOS共源级放大电路，NMOS管作为有源负载；输出级驱动电容负载CL；一个电阻Rz串联电容Cc构成频率补偿电路，本文重点研究频率补偿电路。

米勒补偿技术在共源共栅运放结构中可以有三种具体实现形式，如图2所示。第一种为传统的米勒补偿电容结构，是将补偿电容Cc连接在运放输出节点X与运放第一级输出节点W之间，串联的电阻Rz为消掉右半平面零点；第二种结构是将补偿电容Cc置于输出节点X与输入差分对管M1的漏极节点Y之间；第三种结构是将补偿电容Cc置于输出节点X与第一级电流镜负载的共源共栅管M5的源极节点Z之间；第一种连接方式称为直接米勒补偿电路，第二、第三种称为共源共栅米勒补偿电路[4,5]。

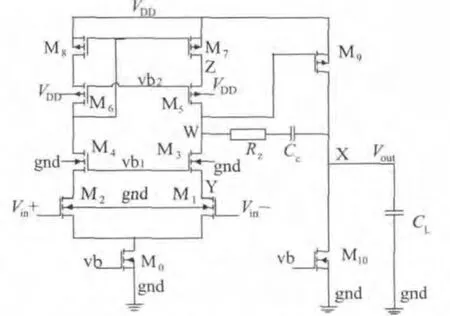
图2 带米勒补偿的两级共源共栅运放

3 小信号电路分析与比较

第一种补偿结构如图2所示，使用带消零电阻的传统米勒补偿电容形式，其等效电路模块和小信号等效电路如图3所示。

图3 使用调零电阻的米勒补偿

其中，忽略差分输入对管M1、M2，共源共栅管M3、M4、M5、M6的体效应，以及除米勒电容和负载电容之外的电路寄生电容。其中RI为第一级等效输出电阻，其大小为Req=（gm5ro5ro7）||（gm3ro3ro1），而RL为输出极点的等效电阻。由小信号等效电路图3（b）所示，可以解得完整的传递函数：

假设，Rz小于RI或者RL，极点相隔较远，则

而有两个极点和一个零点的系统的相位裕度为：

其中，当零点为负，即位于左半平面时，取加号；反之，当零点为正，即位于右半平面时，取减号。而GBW为运放的增益带宽积，是低频增益和主极点的乘积，这里为gm1/Cc。用左半平面零点来部分抵消次极点，来得到足够的相位裕度。

接着分析第二种补偿结构，即将补偿电容Cc置于输出节点X与输入差分对管M1的漏极节点Y之间。其交流等效电路见图4（a），其小信号等效电路如图4（b）所示。其中，同样忽略MOS管的体效应以及除米勒电容和负载电容之外的电路寄生电容，且Rep=gm5ro5ro7。

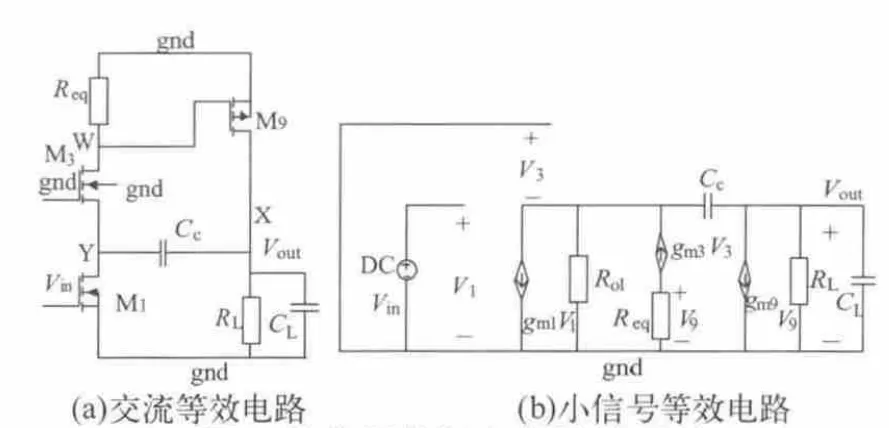
图4 带共源共栅米勒补偿运放

由图5（b）的小信号等效电路可解得其传递函数：

假设，gm9RepCc>>CL且极点相隔很远，则

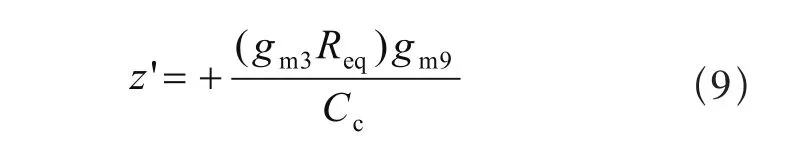
与图2的第一种补偿结构相比，根据式（1）、式（6）和式（2）、式（7）的比较，两者有几乎相同的低频增益和主极点，而比较式（3）和式（8），第二种结构的次极点P2’是第一种补偿结构次极点P2的gm3Req倍，而gm3Req一般大于千倍，故P2’远大于增益带宽积gm1/Cc，由式（5）知其对相位裕度的影响可以忽略，同样的，式（9）右半平面零点和式（8）次极点有相同的数量级大小，远大于增益带宽积，所以也不会影响到相位裕度[6]。

最后，分析第三种补偿结构，即图2中在X点和Z点之间加补偿电容。其交流等效电路和小信号等效电路分别如图5所示。其中，忽略体效应以及除米勒电容和负载电容之外的电路寄生电容，且Req1=ro7。

由图5（b）的小信号等效电路可解得其传递函数：

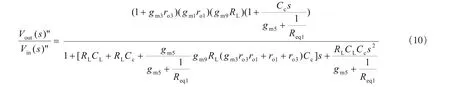
假设，gm9gm3ro3ro1Cc>>CL且极点相隔很远，则

与上述两种补偿结构相比，图5的第三种补偿结构与上述两种补偿结构有相同的低频增益和主极点，从式（12）得到其次极点是第一种结构次极点的gm5gm3ro3ro1倍，因此也远大于其增益带宽积，不会影响相位裕度，而式（13）的左半平面零点会根据与增益带宽积的大小关系，来改善相位裕度。

4 仿真结果和分析

本文所设计的电路采用0.18 μm的CMOS工艺，基于bsim3v3.2的spectre模型，用Cadence的spectre对电路进行仿真，电源电压3 V，负载电容为5 pF。

三种运算放大器补偿结构的波特图仿真结果如图6所示，三种补偿结构的低频增益都为99.2 dB。其中，第一种带消零电阻的直接米勒补偿的单位增益带宽为5.8 MHz，相位裕度为79.2°；第二种共源共栅米勒补偿结构的单位增益带宽为31.9 MHz，相位裕度为96.7°；第三种补偿结构的单位增益带宽为23 MHz，相位裕度为106°。仿真结果符合分析，三种结构都得到了很好的相位裕度，其中共源共栅米勒补偿的两种结构，不需消零电阻，且得到更大的单位增益带宽积和更好的相位裕度。

图5 共源共栅运放第三种补偿结构

图6为三种运算放大器补偿结构的波特图仿真结果。图7为三种运算放大器补偿结构的建立时间仿真结果，当运放输入电压在10 ns内从1.8 V跳变到2.0 V时，输出的瞬态响应结果。从图7中可以看出，三种补偿结果的建立过程都没有明显的电压过冲，其1%的建立时间依次为：120.8 μs、46.9 μs、60.1 μs。与图6的波特图仿真结果相一致。

图6 三种运算放大器补偿结构的波特图仿真结果

图7 三种运算放大器补偿结构的建立时间仿真结果

5 结论

本文对套筒式共源共栅两级运放的三种电容补偿方式进行了电路结构和小信号等效电路分析，得到了三种电路结构的传递函数，并对其零点、极点进行分析和比较，并在0.18 μm CMOS工艺下进行了仿真验证。结果表明，三种电路补偿结构都能够实现很好的频率补偿，但共源共栅米勒补偿的两种结构有更稳定的频率响应特性。由此可以推知，在上述两级运放补偿的设计中，采用共源共栅米勒补偿的两种结构，能用更小的芯片面积实现更优的运放性能。

[1] 拉扎唯. 模拟 CMOS 集成电路的设计[M]. 西安：西安交通大学出版社，2002. 297-305.

[2] Allen PE, Holberg DR. CMOS模拟集成电路设计[M]. 北京：电子工业出版社，2005. 206-225.

[3] Gray P R, Meyer R G. Analysis and Design of Analog Integrated Circuits [M]. 北京：高等教育出版社，2005.606-616.

[4] David B R, Miles A C. Design Techniques for Cascoded CMOS Op Amps with Improved PSRR and Common-Mode Inpur Range [J]. IEEE Journal of Solid-state Circuit,1984, 19（6）：919-926.

[5] 连全文，冯全源. 共源共栅两级运放中两种补偿方法的比较[J]. 微电子学与计算机，2009, 26（7）：191-197.

[6] Willy Sansen. Analog Design Essentials [M]. 北京：清华大学出版社，2008. 150-154.