柔性微型阀对静电驱动振膜微泵压力性能的影响
张 彧 王 文 赵小林 丁桂甫
上海交通大学,上海,200240
0 引言
静电驱动振膜微泵中,腔体内振膜的运行特性会影响微泵的压升性能,而微型阀的存在和运行方式同样会对微泵的性能产生影响。被动式微型阀[1-5]虽然结构简单、应用方便,但其抑制反向流动的效率相对较低。为了提高阀门效率,利用静电驱动的主动微型阀逐渐应用于静电微泵,其中,硅质主动微型阀[6]在多级静电微泵中已取得了良好的效果。由于硅质阀片驱动电压较高,易引起液体电解,因此柔性阀片[7-11]结构受到越来越多的关注,以期在较低的驱动电压下获得较大的阀门开度和输出流量。
目前,关于柔性微型阀的研究主要集中于微型阀自身性能,而针对微型阀对静电微泵压升性能影响的研究很少。因此,本文研究的重点是在静电驱动振膜微泵中引入具有柔性阀片的静电微型阀后,微型阀对振膜微泵的压升性能产生的影响。本文研究的基础是结合最小能量法与均匀压力作用下圆薄膜变形半解析解所建立的静电驱动振膜微泵理论模型,利用其分析微型阀的容积对静电微泵压升的影响,并指出拥有柔性振膜的静电微泵与常规定排量泵在运行方式上的差异。另外,本文基于受力平衡,对一定背压下微型阀的临界封闭电压进行了分析,以此表明柔性阀片结构有利于提高微型阀的可靠性。
1 静电驱动微型阀的结构与运行模式
图1所示为具有微型阀结构的双腔静电驱动振膜微泵。泵包含1张柔性振膜和2个对置的圆拱形腔体,进排气微型阀与腔体结构集成在一个基片上。进气和排气微型阀都可分为具有流动通道的阀体结构和以柔性薄膜为基片的阀片结构。进排气微型阀的阀片结构和尺寸是完全相同的,且阀片与泵腔的振膜集成在同一张薄膜上。但进排气微型阀的阀体结构具有不同尺寸的流动通道,因此二者的工作模式存在差异。
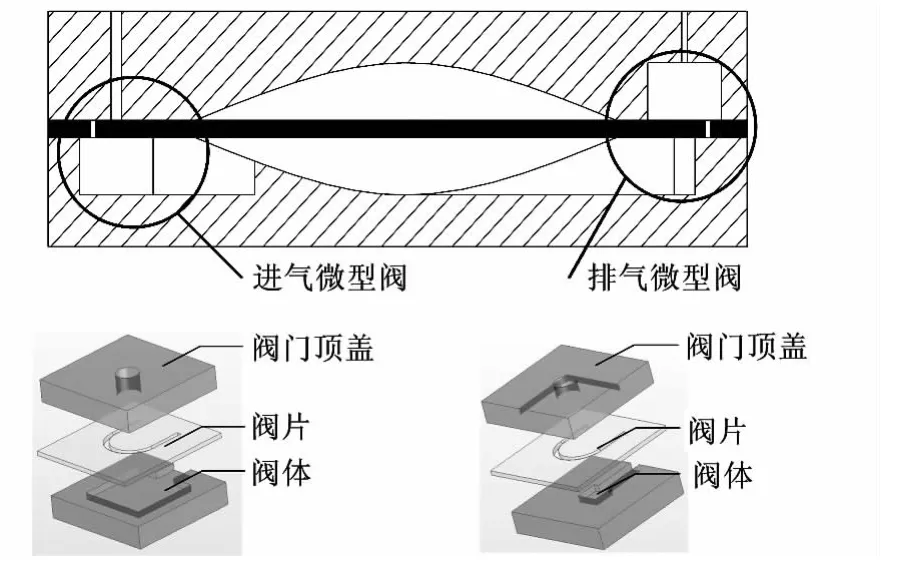
图1 具有微型阀结构的双腔静电微泵
进气微型阀的动作如图2所示。当腔体内的振膜发生压缩动作时,腔体气压升高,当其高于腔外气压时,二者的压差导致进气微型阀关闭。此时,进气微型阀的驱动电压必须与腔体的驱动电压相位相反,这样才不会出现静电力与阀门前后压差相抵消的现象。
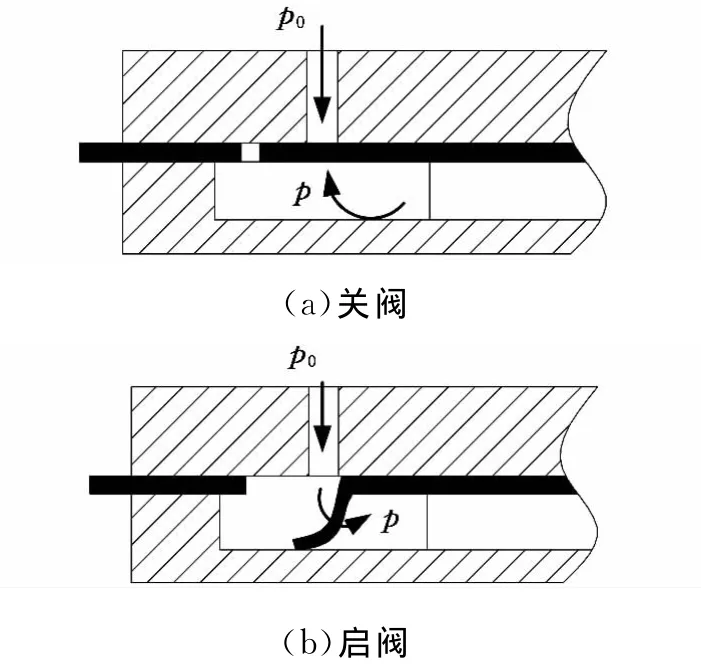
图2 进气微型阀的运行模式
排气微型阀的关闭完全由驱动电压产生的静电力来控制,而其开启则是由阀前后压差的作用来实现的(图3)。为了使微泵的压升尽可能达到其最大理论压升,排气微型阀驱动电压的周期和相位应该与腔体驱动电压完全一致,因此排气微型阀在腔体内的压缩动作结束以前都会一直处于关闭状态。

图3 排气微型阀的运行模式
2 微型阀对静电驱动振膜微泵压升性能的影响
进排气微型阀的存在不可避免地会影响静电驱动振膜微泵的压升性能。由于微型阀容积的引入,微泵的压缩总容积会有一定程度的增大,而有效的压缩动作仅存在于泵腔之中,因此微泵的压升必然会出现一定的变化。
笔者在前期研究中已经建立了针对具有圆拱形简单腔体结构的静电驱动振膜微泵的分析模型[12],预测了静电驱动振膜微泵的最大压升。该模型包含均匀压力作用下圆薄膜变形半解析解和最小能量法两部分,但是只将泵腔空间计入到压缩容积中,并未考虑微型阀对微泵压升的影响。本文中,笔者将微型阀的容积引入到上述分析模型中,用以确定微型阀空间对单腔和双腔微泵压升所产生的影响。修改后的模型与初始模型相比存在两个不同点:①将微型阀的容积计入压缩容积来计算微泵的压升;②最小能量法计算振膜对气体做功时,将微型阀内的气体容积包括在内。
2.1 基本假设
为了简化分析和计算,我们对模型进行一些基本的假设:①薄膜是各向同性的,其物理参数如弹性模量、密度等在薄膜中是均匀分布的;②薄膜在初始状态下是松弛的,不存在初始应力;③膜片厚度远小于膜片直径,因此薄膜的弯曲应力可以忽略,而薄膜的径向应力沿厚度方向是均匀分布的;④膜片与腔体壁面接触是无摩擦的,腔内工质压缩遵循等温压缩过程。
2.2 振膜形状计算
平衡状态下的振膜形状通过均匀压力作用下的圆薄膜大变形半解析解[11]进行计算。图4给出了均匀压力下圆薄膜径向受力平衡和周向受力平衡的状态。圆薄膜变形的控制方程为
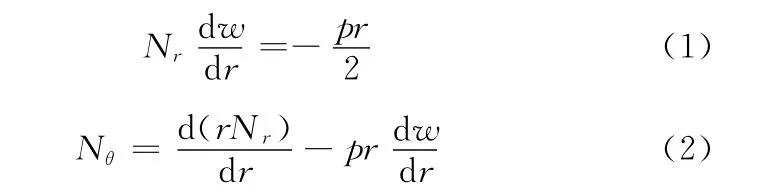
式中,p为薄膜所受的压力;w为薄膜的挠度;r为薄膜半径;Nr、Nθ分别为单位长度的径向合力和周向合力。
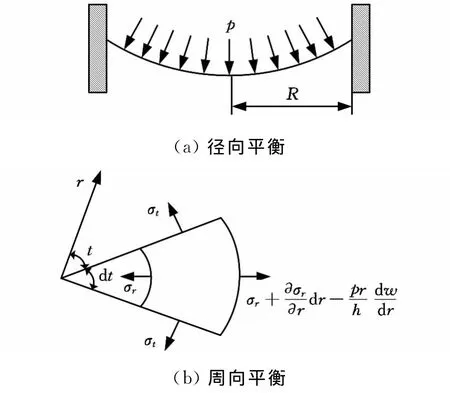
图4 均匀压力下圆薄膜的平衡状态
薄膜的应力应变关系和应变位移关系分别为

式中,εr为薄膜受压力后在径向的应变分量;εθ为薄膜的周向应变分量;u为薄膜的径向位移;h为薄膜厚度;ν为薄膜的泊松比;E为薄膜的弹性模量。
薄膜的四周固定,变形过程中边界位置处的位移和挠度始终为零,因此边界条件为

式中,R为薄膜半径。

通过与Stanford等[13]的实验数据比较可知,针对初始应变为0.044的圆薄膜,当压力为600Pa时,使用半解析解计算得到的薄膜变形型线与实验测量型线的误差均小于1%。

图5 均匀压力作用下的圆薄膜变形半解析解计算结果与实验测试结果的比较
2.3 最小能量法
静电驱动下的泵腔振膜的三部分能量(泵腔振膜的应变能US、泵腔振膜对腔体气体做的功UP、泵腔腔体与振膜之间的静电电容能UC)发生了变化。在泵腔腔体与振膜之间施加驱动电压时,泵腔振膜的这三部分能量都会增大。给定电压下,振膜达到平衡时的条件为dU=dUS+dUP-dUC=0。
为了计算微型阀容积对微泵所能产生的最大压升的影响,我们假定泵腔内振膜进行压缩动作时,进气微型阀由于泵腔内气体压力升高被动关闭,而排气微型阀也在驱动电压作用下同样处于关闭状态。图6、图7分别为具有进排气微型阀的单腔和双腔的微泵处于平衡状态时的示意图。

图6 具有进排气微型阀的单腔微泵平衡状态示意图
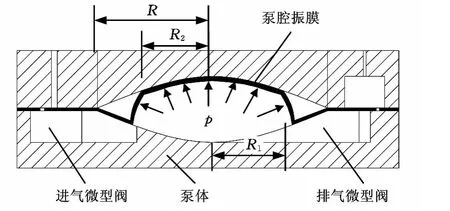
图7 具有进排气微型阀的双腔微泵平衡状态示意图
由于忽略了振膜的弯曲应变,因此膜片应变能仅考虑拉伸应变能,通过对振膜全体积内应变能量密度积分得到

式中,σr为振膜径向拉伸应力。
单腔微泵中的振膜应变εr,s为
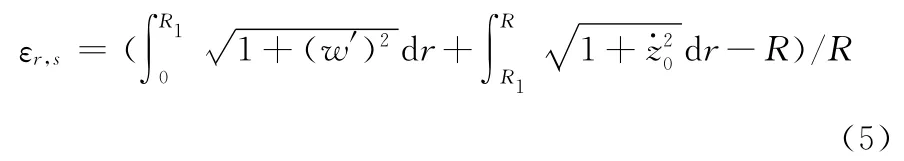
式中,z0为腔体的型线;z·0为腔体型线对半径r的导数;R1为振膜与腔体的贴合半径。
双腔微泵中振膜的应变εr,d为
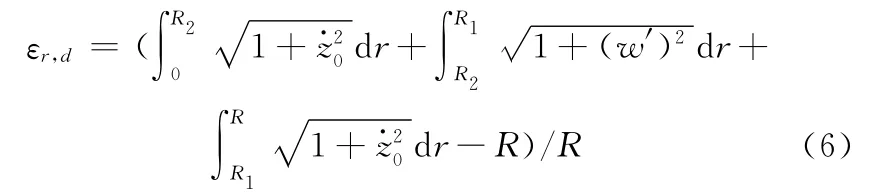
式中,R1为振膜与下腔体的贴合半径;R2为振膜与上腔体的贴合半径。
由于振膜未与壁面贴合区域中,振膜与腔体的间距远大于贴合区域中二者的间距,因此振膜未与壁面贴合区域的电容远远小于贴合区域,在计算振膜与腔体之间的静电电容能时,只考虑二者贴合区域内的电容能:

式中,C为振膜和腔体贴合区域的电容,C=ε0kA/d;k为腔体表面介电层的介电常数;A为振膜和腔体贴合区域的面积;Ua为驱动电压。
单腔微泵中的贴合面积A可以表示为

双腔微泵中,由于上腔体与振膜的电位均为零电势(接地),所以二者之间不存在静电力,因此其贴合面积A也可以由式(8)来计算。
泵腔振膜对气体所做的总功是振膜对泵腔内气体做功与其对泵腔外气体做功的差值。在初始时刻,振膜是水平的,腔内外气体的压力均为p0,泵腔的初始容积为V0,进气、排气微型阀的容积分别为Vi和Vo。施加驱动电压后,泵腔内的振膜逐渐向腔体吸合,导致泵腔内气体被压缩,达到振膜平衡状态时,泵腔空间减小为V,气体压力增大了Δp。由于进气和排气阀门是与泵腔连通的,因此阀门容积内的气体压力也增大了Δp,但是阀门的容积并未发生变化。在泵腔外的气体压力仍为p0的情况下,根据等温压缩假设,微泵内的气体质量守恒可以表示为

由此,可以得到泵腔振膜对腔内气体所做的功:

而振膜对泵腔外的气体做功为

因此,泵腔振膜对气体所做的总功为

单腔和双腔微泵的泵腔初始容积均为
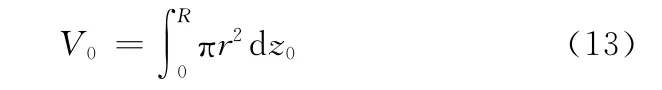
单腔微泵的泵腔压缩终了容积为

双腔微泵的泵腔压缩终了容积为

式中,zup为对置的两个腔体中,上腔体型线的表达式;zlow为下腔体型线的表达式。
通过分析可以看出,无论是单腔微泵还是双腔微泵,考虑微型阀的容积后,泵腔振膜的各部分能量仍然只是由振膜与腔体之间的贴合半径来决定的。
3 排气微型阀的关阀临界电压
由于进气微型阀的运动是被动的,因此我们只针对排气微型阀的临界电压进行分析。根据受力平衡,排气阀的阀片所受到的静电力应与由阀片上下表面的压差形成的气体压力相等,这样才能保证排气阀不会在微泵达到其最大压升前开启。排气微型阀的阀片所受的静电力Fe和气体总压力Fp为

式中,pd为阀片上下表面所受的压差;ε0为真空介电常数;d为介电层的厚度;Ap为阀片与阀体之间的贴合面积;Af为阀体流动通道的投影面积。

4 结果与讨论
为了说明柔性微型阀对静电驱动振膜微泵性能的影响,我们将上述关于微泵压升、微型阀流动阻力的分析模型应用到笔者设计的静电驱动振膜微泵结构中。在单腔微泵中,腔体型线的表达式为z0=4r2,腔体半径为5mm。在双腔结构中,上下腔体结构是对称布置的。因此,单个腔体的初始容积为3.93mm3。腔体表面的介电层为SiO2,其厚度为0.2μm,相对介电常数为3。泵腔振膜和微型阀阀片都由聚酰亚胺薄膜制成,厚度h=13μm,弹性模量E=2.47GPa,泊松比ν=0.3。选择氮气为微泵的工作介质,泵腔内外的初始压力均为0.5MPa。
进气和排气微型阀阀体空间的深度均为100μm。进气微型阀的阀体空间的投影面积为6.25mm2,气流通道入口的阀体截面积为0.25mm2。排气微型阀的阀体空间的投影面积为1mm2,气流通道出口的阀体截面积为0.1mm2。进排气微型阀的气流通道具有相同的结构尺寸,气流通道的长度均为1.7mm,通道截面积均为0.03mm2。因此,进气和排气微型阀的容积分别为0.78mm3和0.2mm3,微型阀的总容积是泵腔腔体容积的24.92%。
4.1 微型阀容积对微泵压升的影响
图8给出了考虑阀门容积时微泵的压升与无阀门情况下微泵的压升,图9所示为考虑阀门后微泵压升较无阀门情况下压升下降的比例。在微泵的压缩容积中加入微型阀容积后,整个压缩容积增大,但有效的静电压缩只是发生在泵腔内,阀门空间中并没有压缩动作,因此必然会使微泵所能产生的压升降低。无论是单腔微泵还是双腔微泵,微型阀容积对其压升的影响均符合这一规律,只是双腔微泵的上腔体限制了振膜的变形,因此微型阀容积所引起的双腔微泵压升减小幅度(4%)低于单腔微泵压升的减小幅度(8%)。在定排量泵中引入阀门容积同样会使泵压降低,但是定排量泵的压升降低幅度明显大于静电驱动振膜微泵。这是由于静电驱动振膜微泵的振膜在泵腔内不同的压力作用下会产生不同的形状,导致其压缩行程发生变化。改变后的压缩行程又会导致微泵的压升发生变化。因此,具有柔性振膜的静电微泵,在引入微型阀容积后,振膜的形状和吸合半径都发生了变化,引起微泵压缩行程的改变,而变化了的微泵压缩行程在一定程度上削弱了容积增大所引起的压升降低。定排量泵的压缩行程是固定的,因此其压升随着微型阀容积变化呈线性减小的趋势。
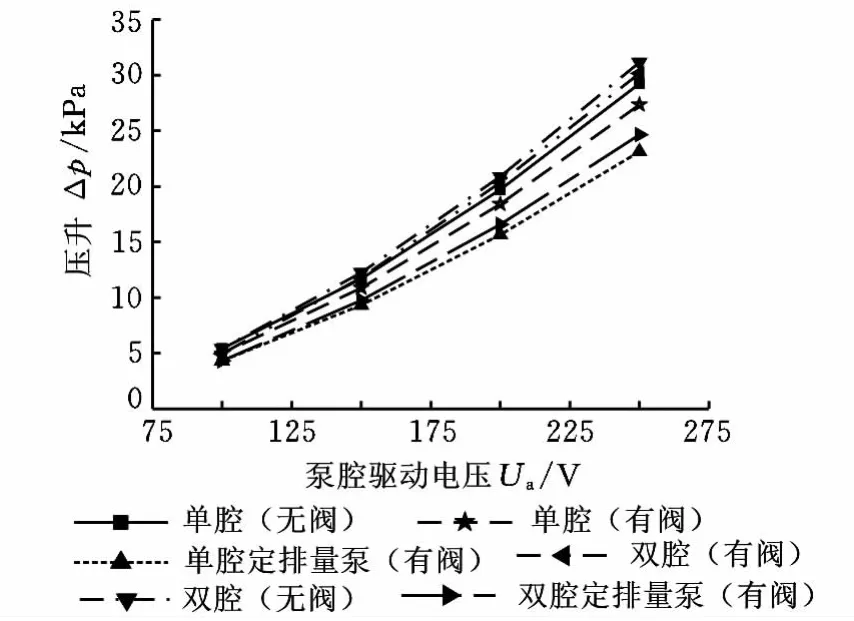
图8 引入微型阀容积后的微泵压升

图9 微型阀容积引起微泵压升的变化比率
4.2 排气微型阀的关阀临界电压
根据本文微型阀结构的设计,阀体气流通道的投影面积为1.04mm2,阀片与阀体之间的电极贴合面积为1.55mm2。当阀体结构表面的介电特性和微泵的压升确定后,单腔和双腔微泵中排气微型阀的临界电压就可以通过计算得到。图10给出了泵腔驱动电压不同时排气微型阀的临界电压。从图10可以看出,排气微型阀的临界电压是远远小于泵腔驱动电压的。由于通过微加工得到的阀体气流通道的边缘比较尖锐,会导致该区域介电层的击穿电压大幅度下降,因此量级较小的排气微型阀的临界电压可以显著提升阀门运行的可靠性。
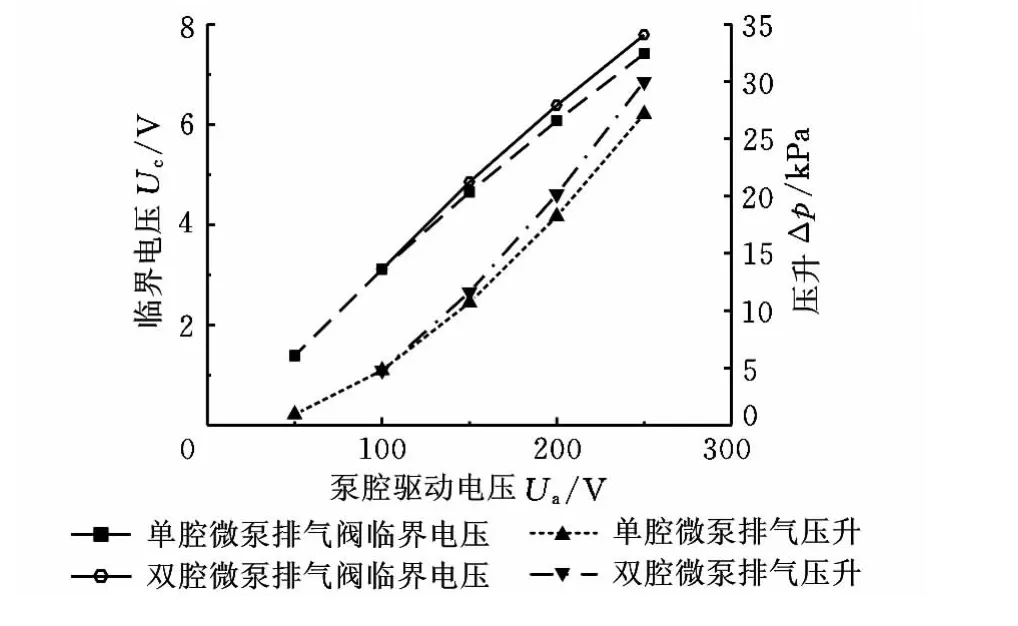
图10 排气微型阀的临界电压
5 结语
本文利用最小能量法与均匀压力载荷下的圆薄膜大变形半解析解相结合的方法,分析了静电驱动的柔性微型阀对静电驱动振膜微泵压升性能的影响。当微型阀的容积约为泵腔容积的24.92%时,单腔微泵的压升降低8%,双腔微泵的压升降低4%。微型阀容积对具有柔性振膜的静电微泵的压升产生的影响远远小于其对定排量泵压升的影响。这是由于柔性振膜的形状与泵腔压升耦合,随泵腔压升变化而改变,在一定程度上抑制了压升的降低幅度。同时,双腔结构对微型阀容积引起的微泵压升降低也有明显的抑制作用。
由于本文设计的微型阀采用的是柔性阀片结构,因此微型阀的关阀临界电压是远远低于静电微泵泵腔驱动电压的,驱动电压的降低极大地提高了排气微型阀及静电驱动振膜微泵运行的可靠性。
[1]Gerlach T,Wurmus H.Working Principle and Performance of the Dynamic Micropump[J].Sensors and Actuators A,1995,50(1/2):135-140.
[2]Koch M,Evans A G R,Brunnschweiler A.The Dynamic Micropump Driven with a Screen Printed PZT Actuator[J].Journal of Micromechanic and Microengeering,1998,8(2):119-122.
[3]Schabmueller C G J,Koch M,Mokhtari M E,et al.Self-aligning Gas/Liquid Micropump[J].Journal of Micromechanic and Microengeering,2002,12(4):420-424.
[4]Dong J X,Lin X Z,Ying J.Coupled Electrostaticstructures-fluidic Analysis of a Nozzle/Diffuser Diaphragm Micropump[J].Advanced Material Research,2011,317/319:1609-1613.
[5]Zengerle R,Ulrich J,Kluge S,et al.A Bidirectional Silicon Micropump[J].Sensors and Actuators A,1995,50(1/2):81-86.
[6]Astle A A,Kim H S,Bernal L P,et al.Theoretical and Experimental Performance of a High Frequency Gas Micropump[J].Sensors and Actuators A,2007,134(1):245-256.
[7]Lee A P,Hamilton J,Trevino J.A Low Power,Tight Seal,Polyimide Electrostatic Microvalve[C]//International Mechanical Engineering Congress &Exposition.Atlanta,1996:17-22.
[8]Goll C,Bacher W,Bustgens B,et al.An Electrostatically Actuated Polymer Microvalve Equipped with a Movable Membrane Electrode[J].Journal of Micromechanic and Microengeering,1997,7(3):224-226.
[9]Zhang Q,Pekas N,Juncker D.Design and Fabrication of Novel Compliant Electrostatically Actuated Microvalves[J]. Advanced Material Research,2009,74:179-182.
[10]王晓浩,周兆英,张文栋,等.聚酰亚胺微型阀及其加工工艺[J].中国机械工程,1999,10(2):136-140.Wang Xiaohao,Zhou Zhaoying,Zhang Wendong,et al.PSPI Passive Microvalve and Its Fabrication[J].China Mechanical Engineering,1999,10(2):136-140.
[11]Yildirim E,Külah H.Analysis and Characterization of an Electrostatically Actuated in-plane Parylene Microvalve[J].Journal of Micromechanic and Microengeering,2011,21(10):105009.
[12]Zhang Y,Wang W.Analytical Model of Electrostatic Actuators for Micro Gas Pumps[J].Microsystem Technologies,2011,17(10/11):1683-1696.
[13]Stanford B,Ifju P.The Validity Range of Low Fidelity Structural Membrane Models[J].Experimental Mechanic,2008,48(6):697-711.

