步进电机矩角关系连续测试方法的研究
余方玉 赵美蓉 林玉池 黄银国
天津大学精密测试技术及仪器国家重点实验室,天津,300072
0 引言
步进电机作为执行元件,是机电一体化的关键产品之一,广泛应用在各种自动化控制系统中。步进电机以脉冲驱动的形式,不需要A/D转换,直接将数字脉冲信号转化成为角位移。与转子位置相关的转矩特性体现了步进电机的实际步进精度[1-3]。理论研究表明,保持状态下步进电机的力矩和转角是一种接近正弦的关系(每个转角周期内出现的力矩最大值称为步进电机的保持力矩)。现有的方法难以实现对这种关系的连续测试,但对这种关系的测试却是步进电机应用和理论研究不可或缺的环节。
目前比较常用的测试方法有加载砝码法、电子称法和砝码-弹簧秤法[4]。加载砝码法原理清晰,实现简单,但只能测得保持力矩,不能获得力矩和转角的对应关系;电子称法和砝码-弹簧秤法无法实现满圆周连续矩角特性测试,且失调角的测试准确度不高。针对矩角关系测试中的难点,本文提出一种新的测试方法,实现步进电机矩角关系的满圆周连续测试。
1 步进电机的电磁力矩数学模型
以两相混合式步进电机为例,在不考虑电机绕组磁滞、磁饱和等现象,忽略电机的绕组互感、高次谐波力矩和定位力矩的情况下,电机的电磁力矩Te可表示为[5-8]

式中,k为电机电磁力矩系数;ia、ib分别为步进电机A相和B相通的电流;zr为电机转子齿数;θ为电机转子位置角。
电机处于保持状态时,ia、ib为常量。对于确定的步进电机,电机转子齿数zr为常量。此时,矩角关系曲线为随位置角θ变化的正弦曲线,周期为

2 步进电机矩角关系测试方法
对步进电机矩角的测试既要测得步进电机转子相对于定子的位置,又要测得该位置电机的电磁力矩。保持状态下,传统的静态测试思路是通过外加驱动力将电机驱动到不同的位置,然后在每个位置测量电机的电磁力矩。这种思路在整圆周内选取一些分离的点进行测试时比较容易实现,却无法进行整圆周矩角关系的连续测试。本文提出一种基于实时力矩平衡原理进行矩角关系测试的方法[9-10],借助驱动机构带动处于保持状态下的步进电机匀速转动,将步进电机看成驱动装置的负载,则驱动力矩和步进电机的电磁力矩相等,对驱动力矩进行实时监测即可实现电磁力矩的连续测试。
根据图1详述该测试方法的力矩传动和角度传递机理。驱动装置带动步进电机匀速转动,角度监测装置和力矩监测装置实时监测传动主轴的位置与力矩。对主传动轴上的传递力矩进行分析,得力矩平衡方程:

式中,T为力矩监测装置上的实测力矩;Te为步进电机的电磁力矩;TJ为由运动引起的惯性力矩;Tf为角度监测装置引起的摩擦力矩;J为负载的转动惯量;α为传动主轴的角加速度。

图1 矩角关系测试方法分析图
测试阶段保证传动轴匀速运动则α=0,即TJ=0。摩擦力矩Tf分两种情况分析,若采用非接触的测角装置,则摩擦力矩不存在,即Tf=0;若采用接触式的测角装置,因为这些装置的动摩擦力矩一般较小,并且可以通过测试获得,然后修正,即有

因此,无论是采用非接触式还是接触式的角度监测装置,摩擦力矩都不会对测试结果造成影响。测试时,驱动装置和步进电机固定,角度传递是一个刚性传递过程,即角度监测装置监测到的传动主轴的角度信息直接反映步进电机转子的位置。由以上分析可知,该测试方法可以实现步进电机矩角关系的满圆周连续测试。
3 步进电机矩角关系测试系统设计
根据测试方法和原理设计步进电机矩角关系测试系统。系统中,角度监测装置选用增量式角度编码器,分辨率为13″;力矩监测装置选用动态扭矩传感器,量程为-20~20N·m,测量精度为0.1%满量程(F.S.);驱动装置选用直流永磁式力矩电机,实现高精度稳速控制;选用数据采集板卡进行数据采集和驱动控制;设计传感器信号处理电路来保证采集卡采集到的测试信号稳定、可靠;在PC机上,开发测量控制软件,对整个测试系统和过程进行控制。测试系统如图2所示。

图2 测试系统实物图
测试系统设计完成后对系统进行调试,检查机械框架、接口的固定及各部分线缆的连接状态,确保框架固定、连接完好。完成后,测试力矩电机、机械框架、扭矩传感器和角度编码器之间的电绝缘状况,保证这些部件之间的电绝缘,切断电磁干扰的耦合路径。安装步进电机前,首先空载运行,测试由摩擦、安装偏心等引起的附加力矩,在测试系统中进行修正。
4 实验及数据分析
测试系统设计完成后,在实验室环境下以常州双杰电机公司生产的两相混合式步进电机130BYG250为被测对象,测试保持状态下步进电机的矩角关系,来验证本文测试方法的正确性。130BYG250步进电机的转子有50个齿,步距角为1.8°,电流为6A时,步进电机保持力矩为20N·m。测试时,步进电机的电流为3.5A。
安装好被测步进电机,使其处于保持状态。设置测试系统的测试参数(主要包括力矩电机带动步进电机运行的转速及角度),测量控制软件控制测试系统按设定参数运行,一次测试完成后可以选择停止矩角关系测试或者重新设置测试参数进行下次测试,下面进行详细的数据分析。
从前述测试方法的分析可知,能否保证驱动装置匀速运行是测试结果正确与否的关键。图3所示为一次测试的角度-时间曲线,测试时设置转速为0.1r/min。从图3可以看出,驱动转速恒定,系统是恒速模式运行。
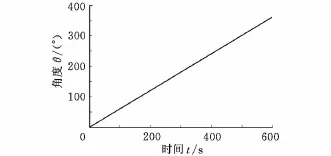
图3 角度-时间曲线整圆周测试图
为了更好地分析驱动转速状况,绘制角度-时间局部曲线,如图4所示。从图4可以看出,方框内的角度-时间曲线不是直线,说明转速在这些位置处有角加速度,则式(4)的惯性力矩不再为零。按式(4)来计算惯性力矩的大小,得总转动惯量远小于1kg·m2,转速波动处角加速度最大值为0.4r/min2,产生的最大惯性力矩为8×10-4N·m。为了分析该力矩对测试结果的影响,绘制综合分析曲线,如图5所示。图5中,直线为角度-时间曲线,类正弦曲线为力矩-时间曲线,方框内对应转速波动区域。从图5可以看出,转速波动处对应力矩-时间曲线上的谷值点位置,力矩范围为9~10N·m,比附加惯性力矩大4个数量级,所以惯性力矩影响可以忽略不计。
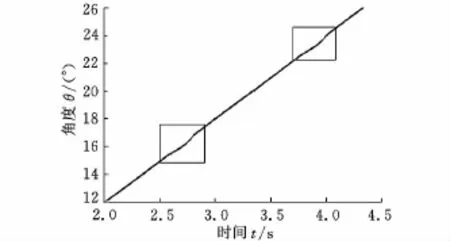
图4 角度-时间曲线(局部)
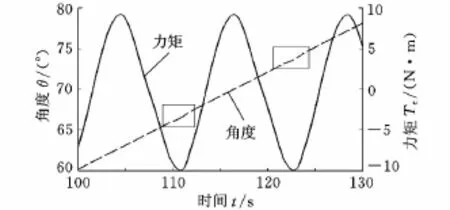
图5 综合分析曲线图
为了验证系统运行的重复性,在相同的测试参数下进行多次的矩角关系测试,测试结果如图6所示。为了进一步验证系统运行状况,在测试电流相同、测试转速不同时进行测试,测试结果如图7所示。从图6、图7可以看出,根据本文方法所设计的系统运行稳定可靠。

图6 相同转速下测试曲线比较
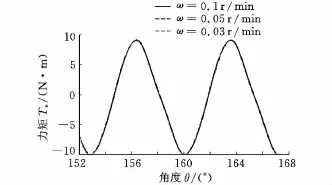
图7 不同转速下测试曲线比较
式(1)说明,在不考虑次要因素时,保持状态下,步进电机的矩角关系曲线是一条正弦曲线。如果文中所提出测试方法是正确的,则实测步进电机矩角关系应该是一个正弦关系。从图6、图7可以看出,测试曲线轮廓接近正弦曲线,为了验证这一点,对测试数据进行拟合,拟合曲线的数学表达式为
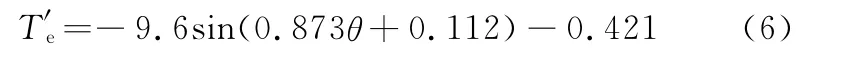
式中,T′e为拟合力矩,N·m。
从式(6)可以看出,拟合曲线为正弦曲线,图8为实测曲线和拟合曲线的比较图。从图8可以看出,实测曲线和拟合曲线基本重合,力矩最大相差0.23N·m,在验证步进电机矩角特性正弦变化规律的同时也验证了所研究方法的正确性。曲线重合度较差的区域出现在力矩变化循环下半个周期,这是由驱动装置的本身性能引起的:力矩上升的半个周期,驱动装置通过闭环控制,能够跟随输出一个缓慢上升的力矩;力矩下降的半个周期,驱动装置无法准确跟随电磁力矩的变化,出现图中曲线不重合的现象。
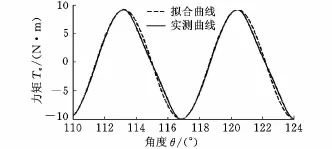
图8 拟合曲线和实测曲线对比图
由式(1)可知,步进电机的矩角关系曲线应该关于角度轴对称,而实测的曲线相当于把理论曲线向下平移0.421N·m,其原因有步进电机内部结构引起的摩擦力矩,或其他部件摩擦、安装偏心引起的附加力矩等。
前文提到,保持状态下,步进电机矩角关系的峰值对应的是步进电机的保持力矩,每个角度周期对应步进电机的齿距角。所以对矩角关系测试数据稍加整理即可得到步进电机的保持力矩,部分数据如表1所示。
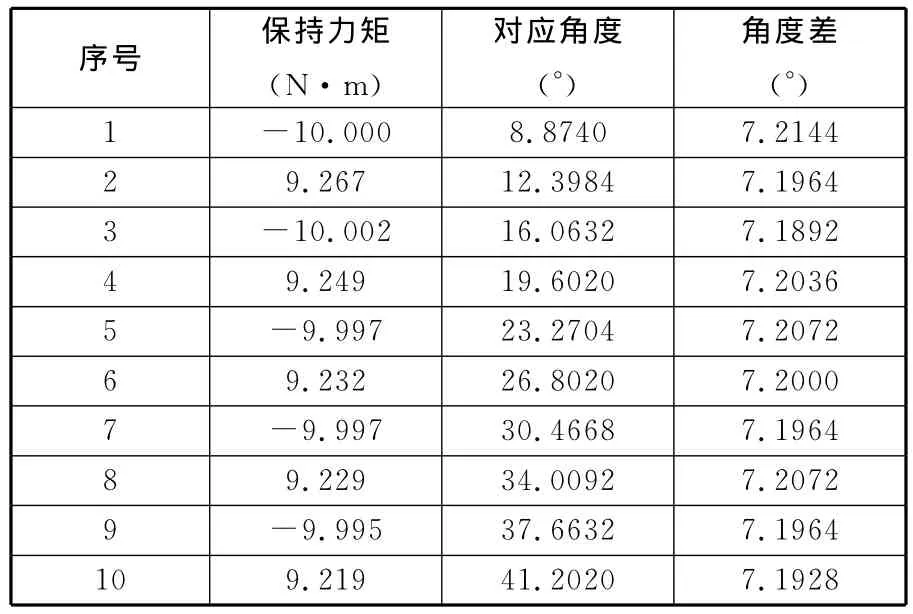
表1 测试数据表(部分数据)
5 结语
本文针对保持状态下步进电机满圆周矩角关系连续测试的难点,提出一种新的测试方法。基于实时力矩平衡原理设计了步进电机矩角关系测试系统,并对一台两相混合式步进电机保持状态下的矩角关系进行了多次测试。测试结果表明,驱动装置能够实现测试方法中稳速控制的要求。所得数据和理论分析值能够较一致,验证了方法的正确性。所设计的系统工作稳定可靠,实现了保持状态下步进电机满圆周矩角关系的连续测试。
[1]尚磊磊,顾永刚,翟超,等.基于LabVIEW的汽车仪表步进电机测试系统[J].电子测量技术,2010,33(12):60-63.Shang Leilei,Gu Yonggang,Zhai Chao,et al.Testing System for Stepper Motor on Auto Meter Based on LabVIEW[J].Electronic Measurement Technology,2010,33(12):60-63.
[2]徐红伟,胥芳,张任.步进电机速度饱和非线性特性分析[J].中国机械工程,2011,22(24):2958-2961.Xu Hongwei,Xu Fang,Zhang Ren.Analysis of Stepper Motor Velocity Saturation Nonlinearity[J].China Mechanical Engineering,2011,22(24):2958-2961.
[3]Tsui W-H K,Cheung C N,Yuen C-W K.Novel Modeling and Damping Technique for Hybrid Stepper Motor[J].IEEE Transactions on Industrial Electronics,2009,56(1):202-211.
[4]张文海.步进电机矩角特性的测试[J].微特电机,1999(2):43-44.Zhang Wenhai.The Torque-angle Characteristic Test of Stepper Motor[J].Micro Electronic,1999(2):43-44.
[5]Ghafari A S,Behzad M.Investigation of the Microstep Control Positioning System Performance Affected by Random Input Signals[J].Mechatronics,2005,15(10):1175-1189.
[6]王凤鸣,刘暾,张鹏顺.步进电动机驱动挠性负载时堵转机理研究[J].中国机械工程,2002,13(9):771-773.Wang Fengming,Liu Dun,Zhang Pengshun.The Mechanism Research on Driving Fiexible of Stepper Motor[J].China Mechanical Engineering,2002,13(9):771-773.
[7]斯祝华,刘一武,黎康.太阳帆板驱动装置建模及其驱动控制研究[J].空间控制技术与应用,2010,36(2):13-19.Si Zhuhua,Liu Yiwu,Li Kang.Research on Modeling and Driver Design of Solar Array Drive Assembly[J].Aerospace Control and Application,2010,36(2):13-19.
[8]肖志权,彭利坤,邢继峰,等.数字伺服步进液压缸的建模分析[J].中国机械工程,2007,18(16):1935-1938.Xiao Zhiquan,Peng Likun,Xing Jifeng,et al.Modeling Analysis of Digital Servo Stepping Hydraulic Cylinder[J].China Mechanical Engineering,2007,18(16):1935-1938.
[9]Pfister P D,Perriard Y.Torque Measurement Methods for Very High Speed Synchronous Motors[C]//International Conferece on Electrical Machines.Vilamoura,Portugal,2008:1-5.
[10]陈寅生.惯性平台框架摩擦力矩测试系统研究[D].哈尔滨:哈尔滨工业大学,2011.

