利用Haskind源格林函数计算规则波中航行舰船的绕射兴波及压力分布

黎 昆，张志宏，顾建农，王 冲

(1.中国人民解放军91388 部队，广东 湛江524022;2.海军工程大学，湖北 武汉430033)

0 引 言

舰船在规则波中航行时，由于入射波浪的作用将会产生摇荡运动。舰船在规则波中摇荡的流体动力计算可分成辐射问题和绕射问题分别加以处理。舰船无航速时(可看作浮体)，如果船体摇荡幅度较小，摇荡兴波也很小，在势流理论范围内，摇荡的定解问题就可以线性化。舰船有航速(即使是等速直线运动)之后，其在波浪上运动的理论分析要比无航速时复杂得多，其中最主要的是受航行兴波与摇荡兴波的干扰。定常移动Kelvin 源格林函数主要用于解决有航速舰船定常兴波问题，而Haskind源格林函数主要解决波浪中无航速或有航速舰船的摇荡问题。相对Kelvin 源格林函数来说，Haskind源格林函数的计算更为复杂。关于如何快速准确计算Haskind 源格林函数及其偏导数，不少学者已对此进行了研究［1-5］。

本文以Wigley 数学船型为研究对象，在理想流体情况下采用微幅波理论，只考虑波浪的绕射问题，通过引入低航速假定来计算波浪与以定常速度移动船体之间的流体动力干扰。基于线性势流理论，利用无限水深三维移动脉动源(Haskind 源)格林函数方法计算规则波中航行舰船的绕射兴波波形及其对应的一定水深处的压力场分布。

1 理论分析

1.1 建立坐标系和定解方程

需要建立2 个坐标系:1)大地坐标系OXYZ，原点O 位于未扰动的水面上;2)随船平动的坐标系oxyz，原点o 位于未扰动的静水面上，x 轴水平指向船首，z 轴垂直向上，y 轴指向船的侧面，构成右手正交系。舰船以固定航速V 沿x 方向行驶，入射波沿－x 方向传播，入射波传播方向与x 轴正向之间的夹角为β(迎浪时β=180°)，如图1所示。

图1 波浪绕船示意图Fig.1 Sketch map of wave flow around ship

根据波浪理论，入射规则波的一阶速度势用复数形式可表示为:

而

假定舰船运动响应与入射波波幅是同阶小量，且经过一段时间后舰船运动已经达到稳定状态，根据线性势流理论，舰船位移向量将作为以遭遇频率ωe(ωe=ω0－k0Vcosβ)为变化频率的简谐量。舰船以定常速度V 沿直线运动时船体将产生移动兴波，相对于随船平动的坐标系oxyz 来说，由定常移动产生的定常兴波速度势可表示为－Vx+Φs(x，y，z)。按照线性势流理论，舰船周围流场中的总速度势由定常势［－Vx+Φs(x，y，z)］和非定常势ΦT(x，y，z，t)两部分组成，如下:

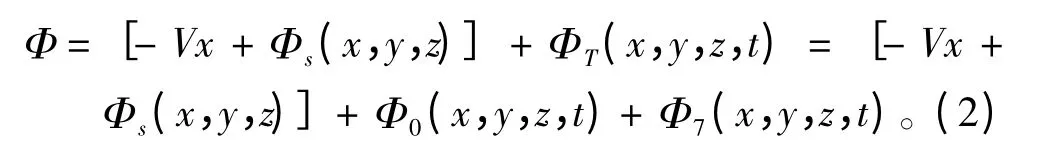
式中:Φs为舰船在静水中恒速航行时引起的定常兴波势(通常假定此部分速度势相对较小，以下忽略其影响);Φ0为已知的入射波速度势;Φ7为待求的绕射波速度势。

由于寻求稳态解，所以采用频域分析方法把时间因素和空间因素分离开来，设绕射势Φ7=Re［φ7(x，y，z)eiωet］，则无限水深水域中绕射势的定解问题可表示为［6］:

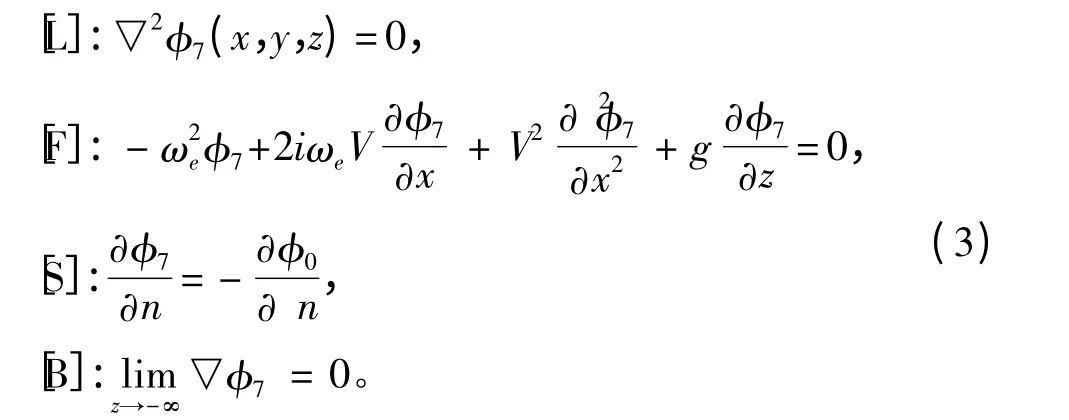
式中:［L］，［F］，［S］，［B］分别为LAPLACE 方程、自由水面边界条件、物面边界条件和水底条件;(x，y，z)为场点坐标;t 为时间;V 为航速;g 为重力加速度;n 为物面外法线矢量(指向船体外部)。

1.2 定解方程的求解

采用分布源法求解上述定解问题，在船体表面上均匀布置Haskind 源，则场点P(x，y，z)处绕射势φ7可表示成积分形式:

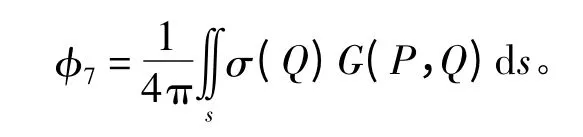
式中:σ(Q)为源点Q(ξ，η，ζ)处的源强密度;G 为Haskind 源格林函数。

将绕射势φ7运用于物面条件可得到用来求解源强密度σ 的积分方程，即:

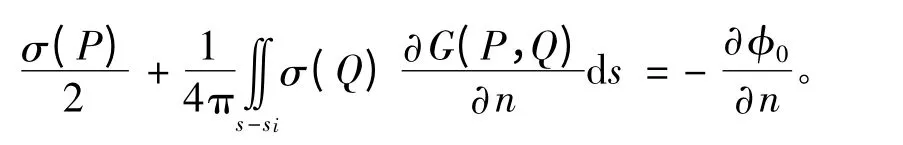
将上述积分方程式进行离散化，化成代数方程组求解［7］。离散方法是把船体表面分成N 个小面元，在标号为n(n=1，2，…，N)的面元上布置等强度且为常数的面源σn，并且在每块小面元上选一控制点Pn，使这些离散的控制点满足边界条件。则上述积分方程可离散化成如下代数方程组:

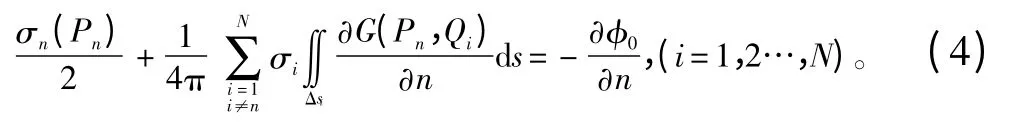
解代数方程组(4)求出源强σ，即可求出流场中任一点的绕射势φ7和速度分布。

1.3 格林函数中奇点的积分处理

求解源强σ 的关键和难点在于如何准确、快速地计算三维移动脉动源(Haskind 源)格林函数G(x，y，z;ξ，η，ζ)。该函数为奇异的二重积分式，求积计算困难费时，被积函数为复变函数且是奇异和振荡的，并且在有的区间成为高频振荡函数，如果处理不好就会导致计算结果出现较大的误差甚至失效。该积分表达式形状复杂、处理繁琐，其表达式原型为:

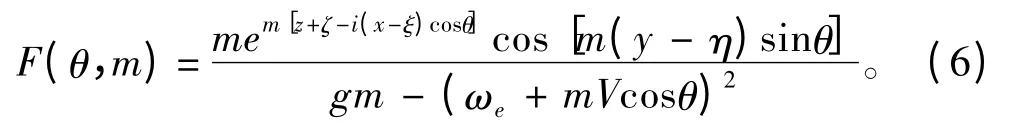
式中:θ 为复波数的幅角;m 为复波数的幅值;ωe为脉动源的振荡圆频率;V 为船速;(x，y，z)和(ξ，η，ζ)分别为场点和源点坐标;g 为重力加速度。

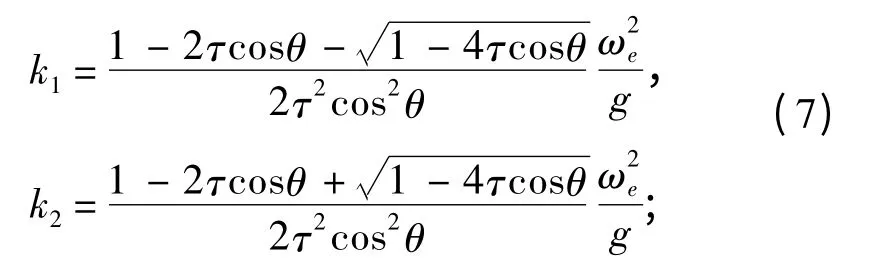
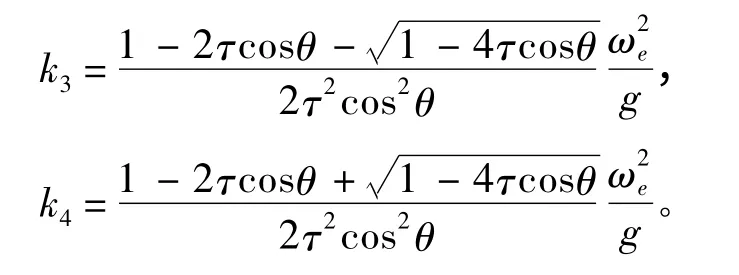
将k3和k4写成在区间上的表达式为:

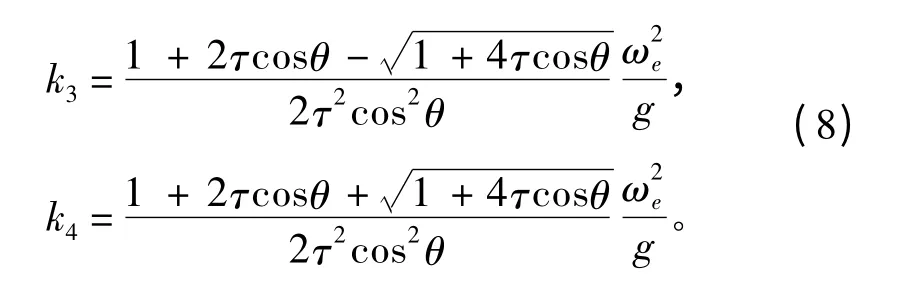
为了使远方辐射条件得以满足，L1和L2分别取为经过k1+iε，k2－iε，k3+iε和k4+iε 绕过k1，k2奇点和k3，k4奇点的积分路径，其中ε 为任意小的正数，积分路径如图2和图3所示。通过整理，被积函数F(θ，m)可表示为:

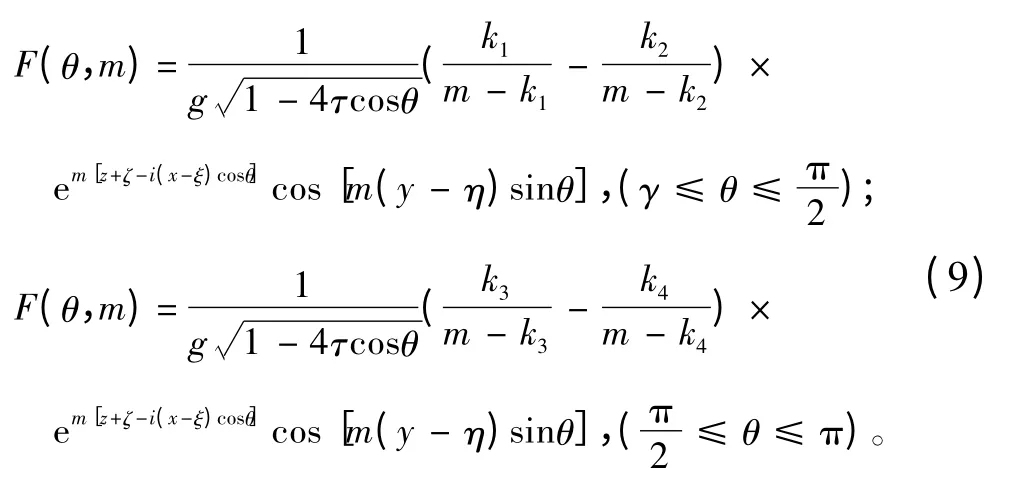
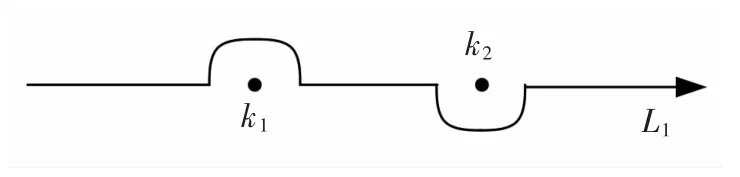
图2 积分路径Fig.2 Inteqral path

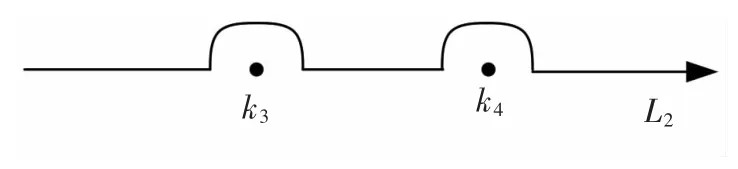
图3 积分路径Fig.3 Inteqral path

令:

x1=(z+ζ)+i［－(x－ξ)cosθ+(y－η)sinθ］，

x2=(z+ζ)+i［－(x－ξ)cosθ－(y－η)sinθ］，

x3=(z+ζ)－i［－(x－ξ)cosθ－(y－η)sinθ］，

x4=(z+ζ)－i［－(x－ξ)cosθ+(y－η)sinθ］。

代入式(5)中进行整理，则格林函数G 中第1个积分项可写为:

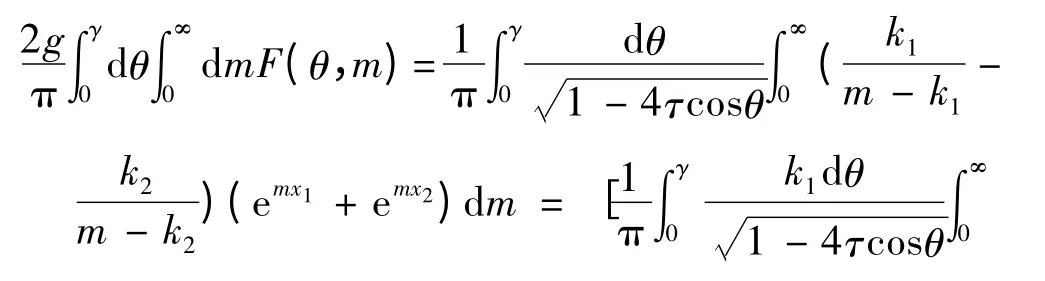
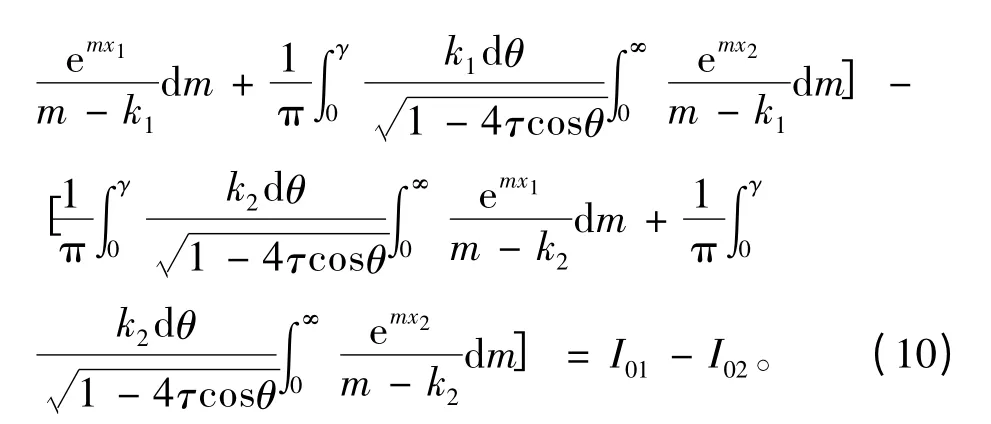
同理，第2 个积分项可写为:

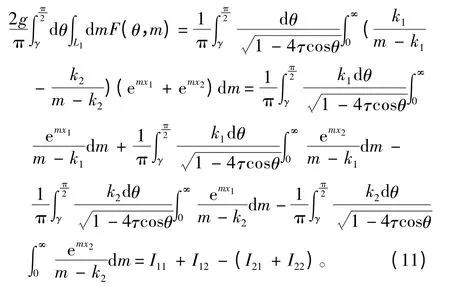
同理，第3 个积分项可写为:

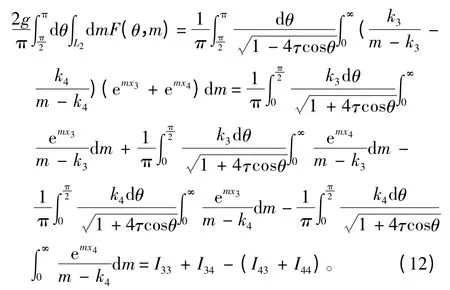
则格林函数G(x，y，z;ξ，η，ζ)可表示为:

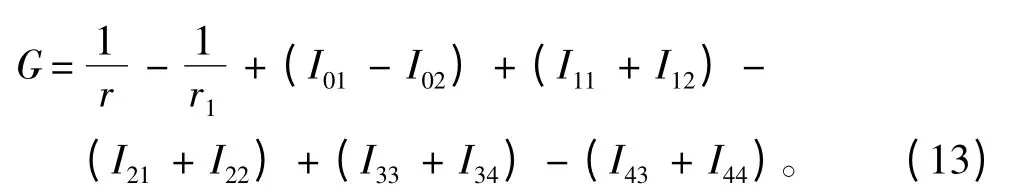
引入复指数积分函数E1(Z)［8］后，Iij的表达式可整理成单积分的形式:

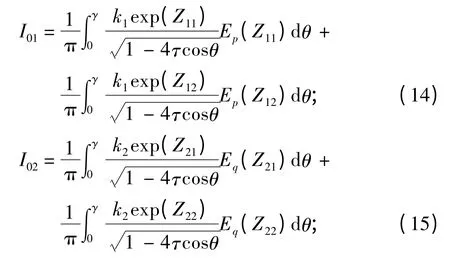
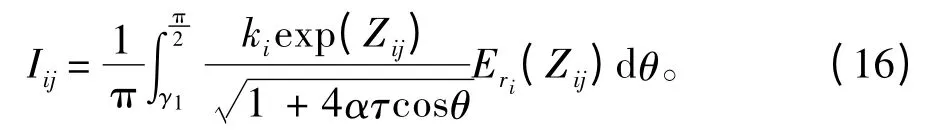
式中:Zij=kixj(i，j=1，2 或i，j=3，4);当i=1，2 时，γ1=γ，α=－1;当i=3，4 时，γ1=0，α=1。

当Re(Z)≥0 时:

Ep(Z)=Eq(Z)=E1(Z);

当Re(Z)＜0，lm(Z)≥0 时:

Ep(Z)=E1(Z)，Eq(Z)=E1(Z)+2πi;

当Re(Z)＜0，lm(Z)＜0 时:

Ep(Z)=E1(Z)－2πi，Eq(Z)=E1(Z);

当lm(Z)≥0 时:

Eri(Z)=E1(Z)，(i=1，3，4)，Eri(Z)=E1(Z)+2πi，(i=2);

当lm(Z)＜0 时:

Eri(Z)=E1(Z)－2πi，(i=1，3，4)，Eri(Z)=E1(Z)，(i=2)。

采用上述变换方法利用复指数函数进行处理后，Haskind 源格林函数计算格式可以成功地处理内层积分中的奇点并将二重积分转化成单积分形式，从而解决了被积函数中奇点的奇异振荡问题。进而采用递推自适应Simpson 法计算变换后的积分会容易很多，且积分是收敛的，并可以大大地减少计算时间。

2 绕射兴波及压力场的计算

解决了Haskind 源格林函数中的奇点问题，即可求解出规则波对以恒定速度航行于其中的舰船引起的绕射势、绕射兴波波形以及水底压力变化。由船舶兴波理论知识可知绕射兴波的表面波形为:

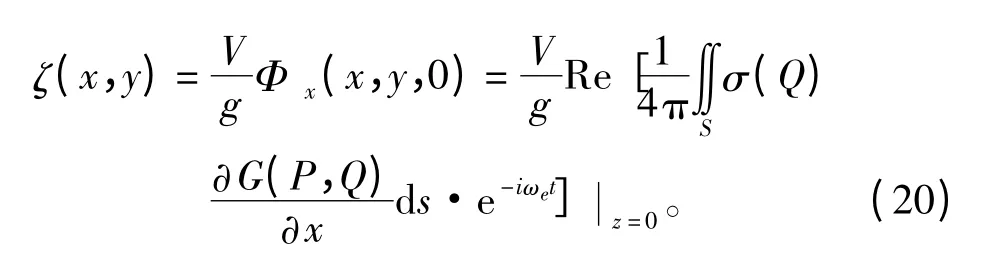
上式中对格林函数G(x，y，z;ξ，η，ζ)求偏导，只需对被积函数F(θ，m)求偏导即可。

由总速度势的分解式(2)可得到距离水面任意点处脉动压力表达式为:

P(x，y，z，t)=Re［p(x，y，z)·e－iωet］。

式中p(x，y，z)=p0(x，y，z)+p7(x，y，z)。

根据伯努利方程，由式(1)可得入射波脉动压力为:

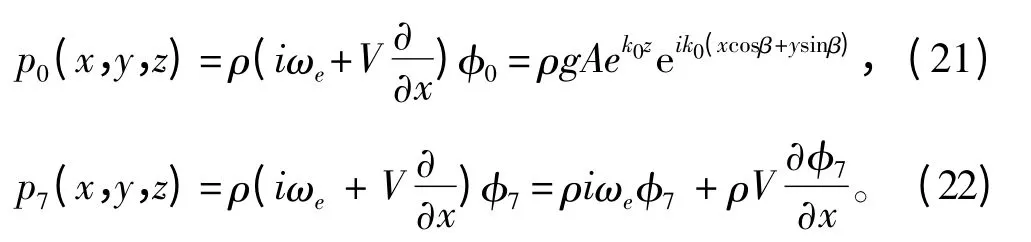
式中:p0为入射波压力;p7为绕射波压力。

图4 波形计算结果与实验结果比较(T0=2.353 s，V=1.0 m/s)Fig.4 Comparison between computed and experimental results of wave pattern when T0=2.353s，V=1.0m/s

图5 压力计算结果与实验结果比较(T0=2.353 s，V=1.0m/s)Fig.5 Comparison between computed and experimental results of pressure when T0=2.353s，V=1.0m/s

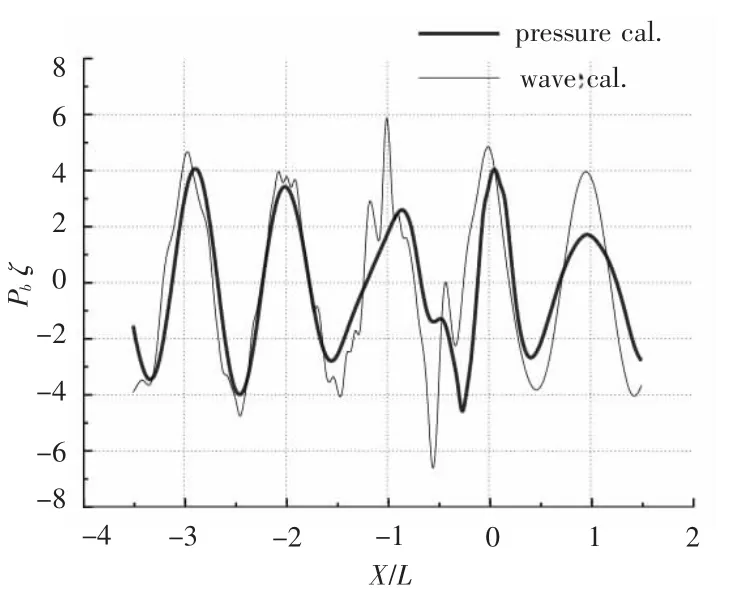
图6 计算波形与对应压力比较(T0=2.353 s，V=1.0 m/s)Fig.6 Comparison between computed wave pattern and it′s corresponding pressure when T0=2.353s，V=1.0m/s

设定初始参数，利用编制程序计算得到横距y=0.25 L 处的绕射波波形、入射波与绕射波的叠加波形及其分别对应的水深h=0.2 L(L 为船长)处的压力变化。在傅汝德数Fh≤0.3 的条件下，设定入射波波幅为3.8 mm，波周期T0=2.353 s，船速V=1.0 m/s，计算得到绕射波与入射波的叠加波形及其对应的压力变化与实验结果比较的曲线，如图4 ～图6所示。图4和图5 中船体位置在(t ≤50 s)附近处，而图6 中船首在(x/L=0.5)处。图中横坐标表示记录的时间t/s，纵坐标表示波高及其引起的水底压力变化ζ，pb(mm H2O)。

另外，在其他条件不变的情况下，改变初始条件，给定入射波波幅为5 mm，波周期T0=2.36 s，船速V=0.8 m/s，利用程序计算得到的波形和压力曲线如图7 ～12所示。图7和图8 中船体位置在(t ≤43 s)附近处，而图9 ～12 中船首在(x/L=0.5)处。

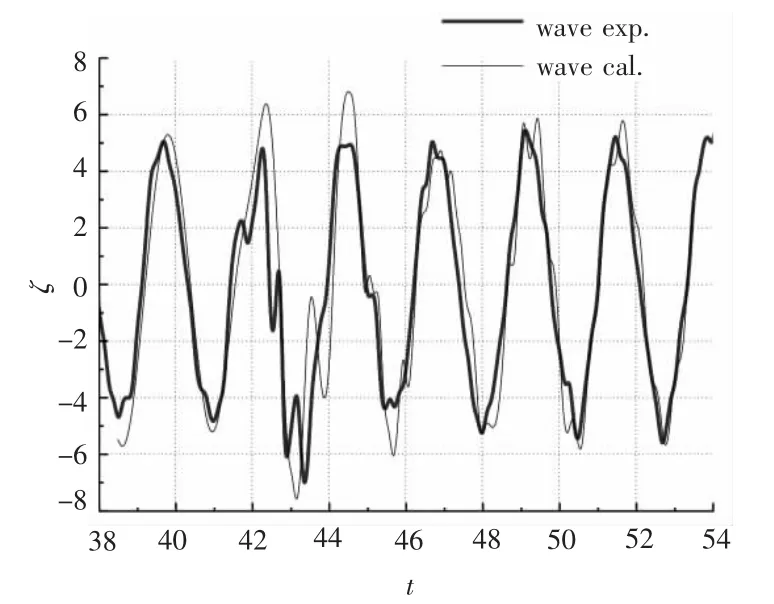
图7 波形计算结果与实验结果比较(T0=2.36 s，V=0.8 m/s)Fig.7 Comparison between computed and experimental results of wave pattern when T0=2.36s，V=0.8m/s

图8 压力计算结果与实验结果比较(T0=2.36 s，V=0.8 m/s)Fig.8 Comparison between computed and experimental results of pressure when T0=2.36s，V=0.8m/s

图9 计算波形与对应压力比较(T0=2.36 s，V=0.8 m/s)Fig.9 Comparison between computed wave pattern and it′s corresponding pressure when T0=2.36s，V=0.8m/s

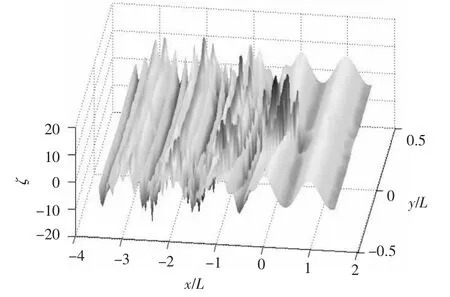
图10 计算波形三维分布图(T0=2.36 s，V=0.8 m/s)Fig.10 Three-dimensional distribution figure of computed wave pattern when T0=2.36s，V=0.8m/s

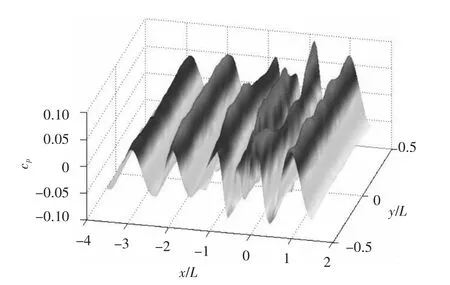
图11 水深h=0.2 L 处压力场三维分布图(T0=2.36 s，V=0.8 m/s)Fig.11 Three-dimensional distribution figure of hydrodynamic pressure field when h=0.2L，T0=2.36s，V=0.8m/s

图12 计算波形等高线图(T0=2.36 s，V=0.8 m/s)Fig.12 Computed wave contour line when T0=2.36s and V=0.8m/s

将绕射波与入射波叠加波形的计算结果和完成的实验结果进行对比，发现二者基本吻合，趋势一致，如图4和图7所示。叠加后的波形在水底引起的压力变化与实验结果相比有一定的误差，这是因为实验结果测量的是舰船航行、船体兴波、入射波和绕射波等因素共同作用引起的水底压力变化，而计算结果只考虑了入射波和绕射波的作用，忽略了舰船航行及船体兴波等因素的影响，因此计算结果和实验结果之间会有所差别，但差别不大，如图5和图8所示。因为低傅汝德数条件下，舰船航行及船体兴波引起的水底压力变化相对为一小量，可忽略不计。在船头前方(x/L=1，－0.3 ≤y/L ≤0.3)附近绕射波形及其对应压力出现了峰谷不对应现象，此时入射波遇到舰船会产生反射，入射波、绕射波、反射波相互影响使船前会出现一定范围的杂波，如图10 ～图12所示。

3 结 语

以上理论和实验研究验证了本文对Haskind 源格林函数中奇点的积分处理方法和编制程序的正确性。在此基础上，改变定解方程满足的物面条件可深入研究航行舰船各个模态辐射势的水动力计算，并可以进一步推广计算随机波中航行舰船辐射势和绕射势引起的水中任一定深处的压力变化。

［1］WAKELING B P，SPROSTON J L，MILLWARD A.Development of a theoretical model of the pressure distribution on a ronnd bilge hull［J］.J.S.R，1986，30(1).

［2］陶建华，吴岩.三维布源法计算大尺度物体波浪力中奇点积分的处理［J］.水动力学研究与进展，1987，2(4):16-22.

TAO Jian-hua，WU Yan.The treatment of singular integrals in the calculation of wave forces acting on a large scale structure with 3- D source distribution method［J］.Journal of Hydrodynamics，1987，2(4):16-22.

［3］WU G X，TAYLOR R E.A green′s function form for ship motions at forward speed［J］.International Shipbuilding Progress，1987，34(398):189-196.

［4］宗智，黄鼎良.三维移动脉动源速度势的数值研究［J］.水动力学研究与进展，1991(6):55-63.

ZONG Zhi，HUANG Ding-liang.Numerical studies on potential of a 3-D pulsating source in uniform stream［J］.Journal of Hydrodynamics，1991(6):55-63.

［5］卢晓平，叶恒奎，张纬康，等.Haskind 源格林函数的奇异性研究与数值积分方法［J］.水动力学研究与进展，1999，14(4):444-452.

LU Xiao-ping，YE Heng-kui，ZHANG Wei-kang，et al.The study on singularity of Haskind-Source Green′s Function and related method of numerical integration.Journal of Hydrodynamics，1999，14(4):444-452.

［6］刘应中，缪国平.船舶在波浪上的运动理论［M］.上海:上海交通大学出版社，1987.

LIU Ying-zhong，MIAO Guo-ping.Theory of ship motion in waves［M］.Shanghai:Shanghai Jiaotong University Press，1987.

［7］黎昆，张志宏，顾建农，等.利用面元法计算舰船在水底引起的压力分布［J］.海军工程大学学报，2011，23(1):43-46.

LI Kun，ZHANG Zhi-hong，GU Jian-nong，et al.Calculating pressure distribution on water bottom caused by a moving ship with panel method［J］.Journal of Naval University of Engineering，2011，23(1):43-46.

［8］MILTON A，IRENE A S.Handbook of mathematical functions with formulas，graphs，and mathematical tables［M］.National Bureau of Standards，Applied Mathematics Series 55，Issued June 1964，Fourth Printing，December 1965，With Corrections.