弹子加压装置接触状态有限元分析

陈文滨，王建吉，兰 海，宁克焱，徐久军

(1.大连海事大学，大连 116026;2.中国北方车辆研究所车辆传动重点实验室，北京 10072)

弹子－弹子盘接触副是制动加压机构的关键部件，具有结构紧凑，便于与片式制动器集成、增力能力强、拆装维护方便和制造成本低等优点.

图1为弹子加压机构的示意图，由转动盘1、弹子2、移动盘3和回位弹簧4组成.当需要制动时，制动力作用于与转动盘相连的拉臂上，使转动盘转动，通过弹子推动移动盘向右移动，将片式制动器压紧，从而使车辆制动.在弹子盘加压机构工作过程中，弹子在转动盘和移动盘的挤压下，在有倾角的圆槽中滚动，将转动盘的旋转运动转化为移动盘的直线运动，同时将作用在转动盘上的力转化为移动盘输出的推力［1］.

图1 弹子盘加压机构示意图

弹子盘加压机构实际传递的力较大，而弹子与转动盘、移动盘的接触面积却很小.这导致在接触区域产生了很大的应力和应变，影响弹子盘加压机构的使用寿命和力传递效率.因此，研究弹子与转动盘、移动盘接触区域的应力应变分布对进一步提高弹子盘加压机构的使用性能、延长使用寿命具有重要的意义.

传统的用于分析接触状态的赫兹接触理论是在许多假设的理想条件下推导出来的，主要适用于点面及线面接触条件下接触区域的应力和应变计算.但是弹子与弹子盘的接触特点为非均匀的弧面接触，运用赫兹接触理论的接触模型进行应力和应变计算的适用性还需要验证.在过去的几十年中，用于接触问题的数值计算方法有了很大发展，其中，有限元法就是其中比较成熟的一种方法［2］，而ANSYS软件是一种具有代表性有限元分析软件.

1 有限元模型

1.1 几何模型

弹子与弹子盘的接触模型如图2所示，由移动盘、转动盘和弹子组成.其中移动盘和转动盘的几何形状完全相同，圆盘半径为64 mm，圆槽半径为13 mm，圆槽所对应的螺旋线的半径为32 mm、升角为α=15°.弹子的半径为12.5 mm.移动盘和转动盘的材料为38CrSi，弹子的材料为GCr15.考虑到几何模型120°圆周对称，则采用对称边界条件，有限元几何模型可简化为图3所示.

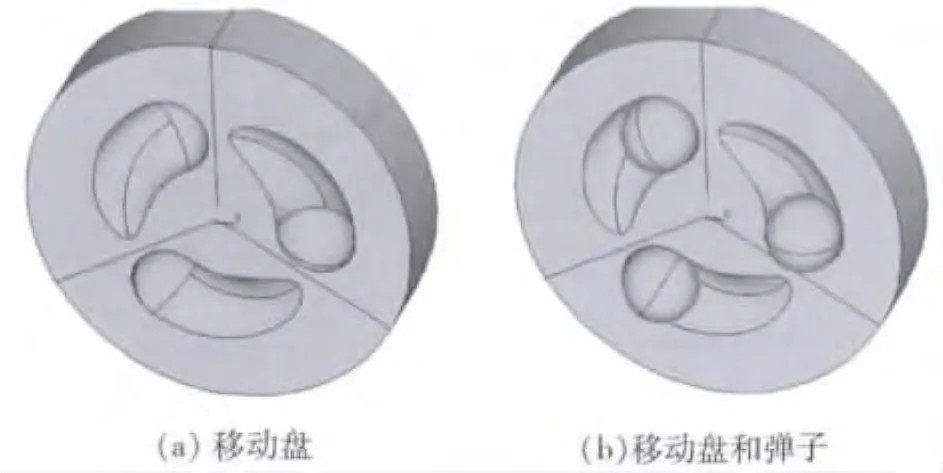
图2 弹子盘几何模型

图3 弹子盘有限元几何模型

1.2 单元类型

单元类型选用SOLID187，是高阶的三维10节点结构实体单元，每个节点有x、y、z方向平动的3个自由度，非常适合生成不规则网络模型，满足弹子盘表面形状复杂等原因而采用自由网格划分的要求.本单元还具有塑性、大变形和大应变等功能.

接触单元选用CONTA174，能与有中间节点的三维实体单元配合使用.CONTA174是三维8节点面面接触单元，可以处理库仑和剪应力摩擦状态.目标单元选用与CONTA174配合的三维目标单元TARGE170.

1.3 网格划分

由于弹子盘表面形状复杂，需选用自由网格划分，与映射法相比，自由网格划分法得到的网格质量较差.但自由网格划分法便于对网格进行局部细化，在应力应变梯度较大的区域形成较密的网格，而在应力应变梯度较小的区域则形成较大的网格，这有利于充分利用计算机资源.网格划分结果如图4所示.

图4 网格划分结果

1.4 接触参数确定

1.4.1 接触面与目标面

ANSYS软件提供了两种接触对设置方式，可以将接触形式设置为对称接触对接触或者非对称接触对接触.根据弹子与弹子盘的实际接触情况，可以将其接触形式设置为非对称接触对接触.对于非对称接触对接触，需要将相互接触表面中的某一个表面视为目标面，而把另一个作为接触面.这两个面结合起来形成接触对.在计算过程中，程序会检测接触单元侵入目标面的穿透量，而不会检测目标单元侵入接触面的穿透量.因此，正确选择接触面和目标面能够使接触模型更符合实际接触状况，计算结果更合理.在选择接触面和目标面时，有一些常用的判断标准［3］.根据这些判断标准，将弹子表面设置为接触面，弹子槽表面设置为目标面.

1.4.2 法向接触刚度

对于有限元接触问题，接触刚度是一个很重要的参数，它和实体单元刚度一起决定了接触单元的刚度.在通常情况下，接触刚度越大，两个接触表面之间的渗透量就会越小，所得到的计算结果就越符合实际情况.但是，过大的接触刚度会引起总刚度矩阵的病态，造成收敛困难.ANSYS采用实常数来定义接触刚度，取值通常在0.01到10之间，实际计算时先取一个较小的值，然后不断增大，直到前后两次计算结果差别很小或者发生不收敛.在本文的分析中，经过反复尝试，确定接触刚度取100时计算结果更合理且不会引起有限元模型收敛困难，比较合适.

1.4.3 初始接触状态

在有限元静力分析中，如果模型中存在接触约束，但是接触对的初始接触状态不正确，会导致程序无法识别该接触对的接触约束，导致模型发生刚体运动，从而引起错误使计算终止.ANSYS软件要求接触模型中的接触对在开始进行计算时两个接触面必须“刚好接触”，否则就无法识别该接触约束.但实际上，很难保证所建立的有限元模型接触对“刚好接触”.这是因为，即使实体的几何模型在建立时是“刚好接触”的状态，由于在进行网格划分对模型进行离散化时存在数值舍入误差，得到的有限元模型与几何模型的表面尺寸必然会有细微差别，导致目标面和接触面的单元网格之间会产生小缝隙，或者发生过大的初始穿透，使其不能“刚好接触”.在这种情况下，会导致计算结果不收敛.

因此，定义接触对的初始接触状态是建立有限元接触分析模型的一个最重要的部分.为了使接触对能够“刚好接触”，在建立弹子加压装置有限元模型时，有意使弹子表面与弹子槽表面有一个较小的间隙.然后，设置接触单元的选项keyopt(5)=1，即ANSYS软件自动提供一个使接触面向目标面偏移的量，来使接触对在初始状态下“刚好接触”.

1.5 边界条件设定与加载

边界条件设定与加载见图5，将移动盘底部的自由度全部约束，将转动盘底部沿z方向的自由度约束.再给转动盘施加一个绕z轴正方向的扭矩M=115 N·m.

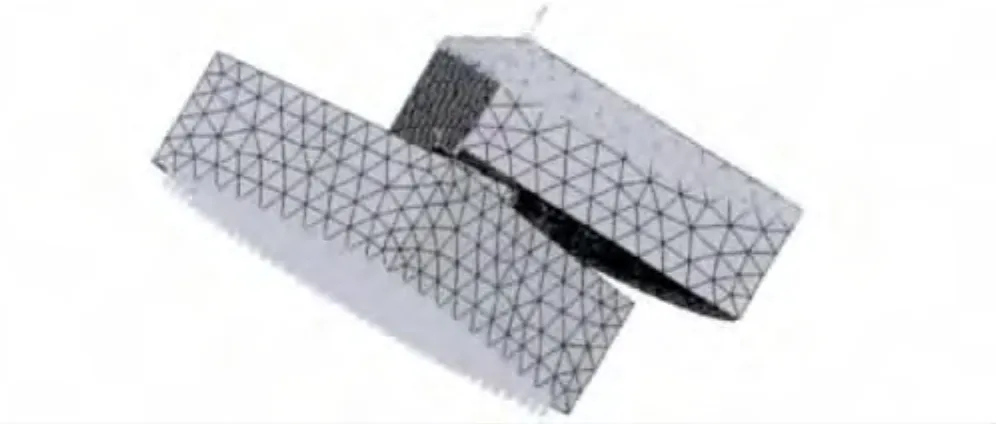
图5 边界条件与加载方式

2 计算结果与分析

2.1 最大挤压应力分布

弹子与弹子槽接触区域的挤压应力分布如图6所示，图中的应力拉伸方向为正，压缩方向为负.可见弹子槽上的最大挤压应力出现在接触区域中心，其值为1.4 GPa.弹子上的最大挤压应力也出现在接触区域中心，其值为1.32 GPa.接触区域沿着弹子槽宽度方向分布较宽，接触面积远远大于点面赫兹接触模型的接触面积，有效地降低了弹子和弹子盘的最大接触应力，提高了接触副的承载能力.

图6 接触区域挤压应力分布

2.2 接触变形的计算结果与试验结果、赫兹接触模型计算结果的比较

接触区域的变形量是指相互接触的弹子与弹子槽底面在载荷作用下发生变形，引起的弹子槽法向距离的变化.为了验证所建立的有限元模型计算结果的合理性，将有限元计算结果与模拟试验的试验结果和赫兹接触模型［4］的计算结果进行了对比，结果见图7.由图7可见，当载荷 (输出推力)增大，变形量总体呈线性增加，在5 kN到40 kN的范围内，有限元计算结果与实测结果吻合较好，其中在20 kN时偏差稍大.这说明弹子盘机构有限元模型及计算结果是合理的.但采用赫兹公式的计算结果与实测值偏差较大，载荷越大，偏差也越大.说明采用赫兹模型计算弹子与弹子盘的接触变形存在明显的不合理性.

图7 移动盘输出推力与变形量的关系

造成赫兹接触模型计算结果偏高的原因是弹子和弹子槽的半径很接近，接触弧长较大，不满足赫兹接触模型中与受载物体的曲率半径相比接触面积尺寸很小的假设［5］.这导致实际的接触面积要比赫兹接触模型估计的要大，因而得到的变形量偏大.

3 结论

1)有限元仿真计算结果与试验结果均表明，当载荷达到40 kN时，最大接触变形可达40 μm，弹子盘的最大接触应力为1.4 GPa，弹子的最大接触应力为1.32 GPa，均在弹性范围内.

2)对于弹子与弹子盘的接触，采用经典的赫兹接触模型的计算结果与有限元仿真计算结果和实测结果存在较大的偏差，说明经典赫兹接触模型并不适用于弹子和弹子槽的接触分析，应对其进行修正.

［1］张洪图，姜正根，赵家象.坦克构造学 ［M］.北京:北京工业学院出版社，1986.

［2］王晓春，孔祥安.接触力学及其计算方法 ［J］.西南交通大学学报，1996，(6):230-233.

［3］王 槐，张景旭，代 霜.运用ANSYS的平面止推轴承有限元分析 ［J］.现代制造工程，2011，(8):75-79.

［4］瓦伦丁L.波波夫.接触力学与摩擦学的原理及其应用 ［M］.北京:清华大学出版社，2011.

［5］K.L.Johnson.Contact mechanics［M］.Cambridge University Press，1985.